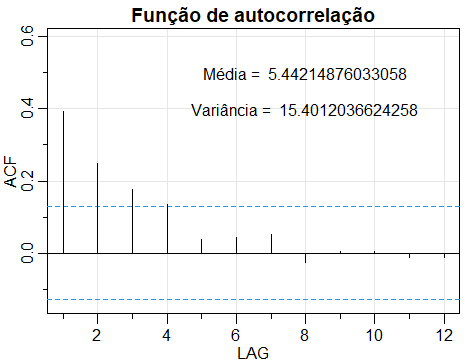
Figura II.1: Função de autocorrelação da série de vendas de sabão.
Aplicando uma mistura de distribuições discretas à série de vendas de sabão, como mostrado na Seção I.1, pode-se pensar em alguns estados subjacentes não observados que determinam de qual componente da mistura extrair uma observação. Em um modelo de mistura independente, esses estados ou as observações, respectivamente, devem ser independentes. No entanto, esse não é o caso da série de vendas de sabão, como pode ser visto na figura abaixo, que mostra a função de autocorrelação dessa série.

Figura II.1: Função de autocorrelação da série de vendas de sabão.
A figura acima revela que as observações de vendas de sabão estão significativamente correlacionadas entre um a três, indicando dependência serial na série. Assim, uma mistura independente não é um modelo apropriado aqui, pois não considera todas as informações contidas nos dados e deve-se pensar em modelos alternativos. Uma maneira de modelar séries de dados de contagem com correlação serial é aplicar um Modelo Oculdo de Markov Poisson, que é um caso especial de uma mistura dependente. Portanto, nas seções a seguir, o Modelo Oculto de Markov (HMM) básico e suas propriedades, como distribuições marginais, momentos e verossimilhança, serão introduzidos.
Mais uma vez, gostaríamos de salientar que o desconhecimento de qualquer covariável da séries de vendas de sabão influencia a seleção de um modelo apropriado. Pode muito bem ser que a correlação serial observada se deva a algumas covariáveis, como preço. Assim, considerando as covariáveis, podem existir modelos mais apropriados que um HMM, embora covariáveis também possam ser considerados no HMM, como será mostrado na Seção VI.4.
Seja \begin{equation} \{S_t\} \, = \, \{S_t , t=1,2,\cdots\} \,= \, \{S_1,S_2,\cdots \} \end{equation} denotando a sequência de observações, \begin{equation} \{C_t\} \, = \, \{C_t , t=1,2,\cdots\} \,= \, \{C_1,C_2,\cdots \} \end{equation} uma Cadeia de Markov definida no espaço de estados \(\{1,2,\cdots,m\}\), \begin{equation} S^{(t)} \, = \, \{S_i , i=1,2,\cdots,t\} \,= \, \{S_1,S_2,\cdots,S_t \} \qquad \mbox{e} \qquad C^{(t)} \, = \, \{C_i , i=1,2,\cdots,t\} \,= \, \{C_1,C_2,\cdots,C_t \} \end{equation} suas histórias até o tempo \(t\), respectivamente. Considere um processo estocástico que consiste em duas partes, primeiro o processo paramêtrico subjacente, mas não observado, \(\{C_t\}\), que possui a propriedade Markov \begin{equation} P(C_t \, | \, C^{(t-1)}) \, = \, P(C_t \, | \, C_{t-1}), \end{equation} e segundo, o processo dependente do estado \(\{S_t\}\), para o qual se mantém \begin{equation} P(S_t \, | \, S^{(t-1)},C^{(t)}) \, = \, P(S_t \, | \, C_{t})\cdot \end{equation}
Então, o processo estocástico \(\{S_t\}\) é chamado de Modelo Oculto de Markov de \(m\)-estados. A segunda propriedade é chamada independência condicional e significa que, no caso de \(C_t\) ser conhecido, \(S_t\) depende apenas de \(C_t\) e não de estados ou observações anteriores. Aqui e no seguinte, se não indicado de outra forma, utilizamos MacDonald & Zucchini (1997) como uma referência padrão. A estrutura básica do HMM é ilustrada na figura a seguir.
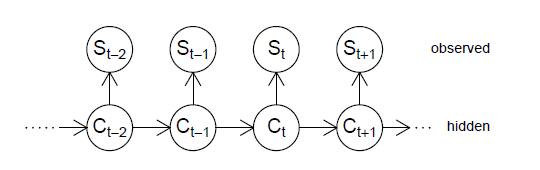
Figura II.2: Estrutura básica de um HMM (Zucchini & MacDonald, 2009).
Um Modelo Oculto de Markov \(\{S_t, C_t \, : \, t\in \mathbb{N}\}\) é um tipo particular de mistura dependente, com \(S_t\) e \(C_t\) representando representando duas séries temporais tais que: \begin{equation} P(C_t \, | \, C^{(t-1)}) \, = \, P(C_t \, | \, C_{t-1}), \qquad t=2,3,\cdots \end{equation} é uma Cadeia de Markocv e \begin{equation} P(S_t \, | \, S^{(t-1)},C^{(t)}) \, = \, P(S_t \, | \, C_{t}), \qquad t\in\mathbb{N}\cdot \end{equation}
Assim, um Modelo Oculto de Markov ou HMM é uma combinação de dois processos, uma Cadeia de Markov que determina o estado no tempo \(t\), \(C_t = c_t\), e um processo dependente do estado que gera a observação \(S_t = s_t\) em dependência do estado atual \(C_t = c_t\). De fato, para cada estado possível do espaço de estados \(\{1,2,\cdots,m\}\) temos uma distribuição diferente para \(S_t\).
Em geral, \(\{C_t\}\) pode ser qualquer Cadeia de Markov, no entanto, neste trabalho, assumimos que a Cadeia de Markov é homogênea e irredutível com a matriz de probabilidades de transição \(\Gamma\). Pela irredutibilidade do \(\{C_t\}\), existe uma distribuição estacionária única da Cadeia de Markov \(\delta\), para obter detalhes, consulte a Seção I.2. Vamos supor, salvo indicação em contrário, que \(\{C_t\}\) é estacionária, de modo que \(\delta\) é para todo \(t\) a distribuição de \(C_t\).
Observe que um HMM é uma construção bastante teórica. Na realidade, apenas o processo dependente de estado \(\{S_t\}\) é observado enquanto a Cadeia de Markov subjacente \(\{C_t\}\) permanece desconhecida ou oculta. No entanto, em muitas aplicações, há uma interpretação razoável para os estados subjacentes. Considere, por exemplo, que a série de retorno diários introduzidas na Seção I.1 são modeladas com um HMM de dois estados. Então, os estados da Cadeia de Markov subjacente podem ser interpretados como estados gerais do mercado financeiro, ou seja, um estado com baixa atividade comercial e um estado com alta atividade comercial.
O processo que gera as observações de um HMM de dois estados é demonstrado novamente na Figura II.3.
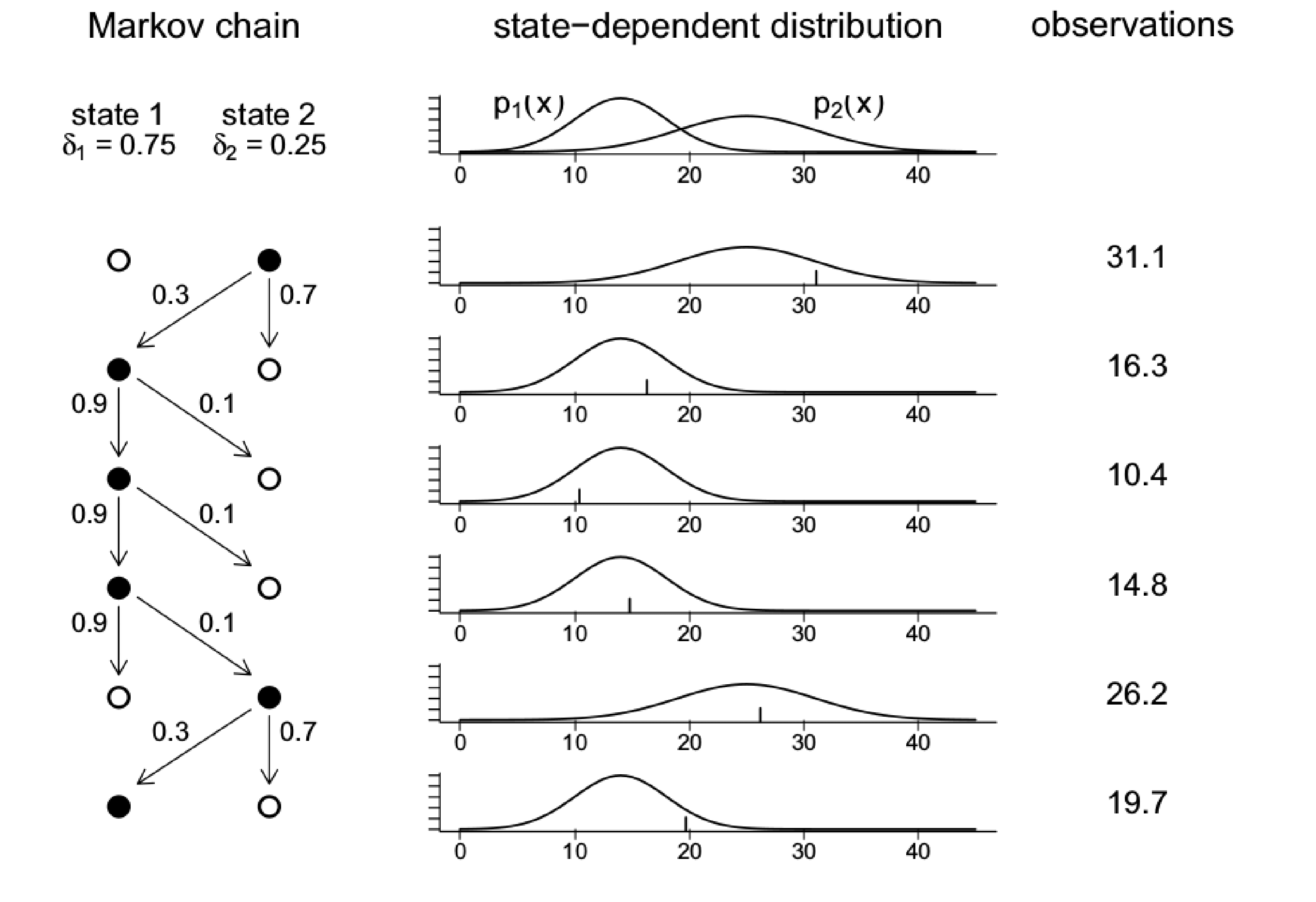
Figura II.3: Estrutura do processo HMM de dois estados (Zucchini & MacDonald, 2009).
Em contraste com a Figura I.2, que mostrou a estrutura do processo de um modelo de mistura independente de dois componentes aqui, as probabilidades para o estado \(C_{t+1}\) dependem do estado \(C_t\), pois o processo paramétrico é modelado através de uma Cadeia de Markov. No entanto, como no caso de misturas independentes para cada estado, existe uma distribuição diferente, dependente do estado, para a variável aleatória \(S_t\) no tempo \(t\), discreta ou contínua, como mostra a Figura II.4.
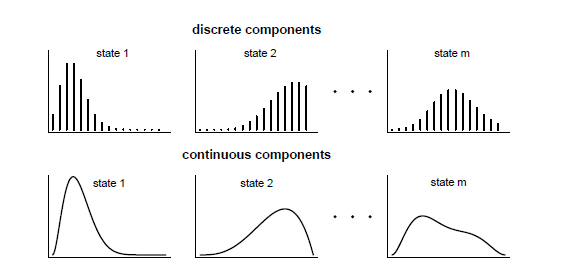
Figura II.4: Distribuições componentes de um HMM (Zucchini & MacDonald, 2009).
Pode-se pensar em qualquer distribuição possível para modelar as distribuições dependentes do estado. Por exemplo, assumindo distribuições de Poisson como distribuições dependentes do estado, produz um HMM Poisson. Se as distribuições dependentes do estado seguem uma distribuição normal, obtém-se um HMM normal. É até possível ter diferentes famílias de distribuições para diferentes estados.
A notação para as distribuições dependentes do estado deve ser introduzida em detalhes. Seja \(C_t\) o estado da Cadeia de Markov no tempo \(t\), \(S_t\) denota a distribuição dependente do estado no tempo \(t\) e \(s\) é qualquer realização possível de \(S_t\). Então, no caso de componentes discretos, usamos a seguinte notação para a distribuição dependente do estado: \begin{array}{ccc} C_t \, = \, 1 & & p_1(s) \, = \, P(S_t=s \, | \, C_t=1) \\ C_t \, = \, 2 & & p_2(s) \, = \, P(S_t=s \, | \, C_t=2) \\ \vdots & & \vdots \\ C_t \, = \, m & & p_m(s) \, = \, P(S_t=s \, | \, C_t=m) \cdot \end{array}
Portanto, \(p_i(s)\), \(i\in\{1,2,\cdots,m\}\) representa a distribuição de \(S_t\) dado que \(C_t = i\). Observe que, em geral, é necessário adicionar outro índice para o tempo \(t\), ou seja, escrever \(p_{t,i}(s)\), no entanto, como assumimos que as distribuições dependentes de estado não mudam ao longo do tempo, omitimos o índice de tempo neste artigo.
A notação para o caso contínuo é semelhante: \begin{array}{ccc} C_t \, = \, 1 & & f_1(s) \, = \, f(S_t=s \, | \, C_t=1) \\ C_t \, = \, 2 & & f_2(s) \, = \, f(S_t=s \, | \, C_t=2) \\ \vdots & & \vdots \\ C_t \, = \, m & & f_m(s) \, = \, f(S_t=s \, | \, C_t=m) \cdot \end{array}
Novamente, omitimos o índice para o tempo \(t\).
Considere um Modelo Oculto de Markov \(\{S_t, C_t \, : \, t\in \mathbb{N}\}\) com distribuições dependentes de estado Poisson de parâmetros 1, 5 e 10, isto é, no estado 1 a observação \(S_t\) têm distribuição \(Poisson(1)\), no estado 2 a observação \(S_t\) têm distribuição \(Poisson(5)\) e no estado 3 a observação \(S_t\) têm distribuição \(Poisson(10)\). Considere também a matriz de probabilidades de transição \begin{equation} \Gamma \, = \, \begin{pmatrix} 1/3 & 1/3 & 1/3 \\ 2/3 & 0 & 1/3 \\ 1/2 & 1/2 & 0 \end{pmatrix}\cdot \end{equation}
Vamos utilizar o pacote R HiddenMarkov escrito e mantido por David Harte. Neste pacote de funções vamos utilizar duas delas: dthmm, a qual cria um objeto tipo HiddenMarkov a tempo discreto e a função simulate, a qual permite obter o processo simulado.
Com o comando str mostramos a estrutura de qualquer objeto R. Na variável x temos a resposta simulada, em Pi temos a matriz de probabildiades de transição informada da Cadeia de Markov subjacente, em delta indicamos a distribuição incial da Cadeia de Markov, distn indica-nos a distribuição da resposta, pm é o vetor de parâmetros das distribuições da resposta e y guarda os estados simulados da Cadeia de Markov subjacente.
Mostraremos agora a estimação dos parâmetros \(\lambda\) das três distribuições Poisson envolvidas na simulação, fazemos isto para que possamos perceber a qualidade dos dados simulados.
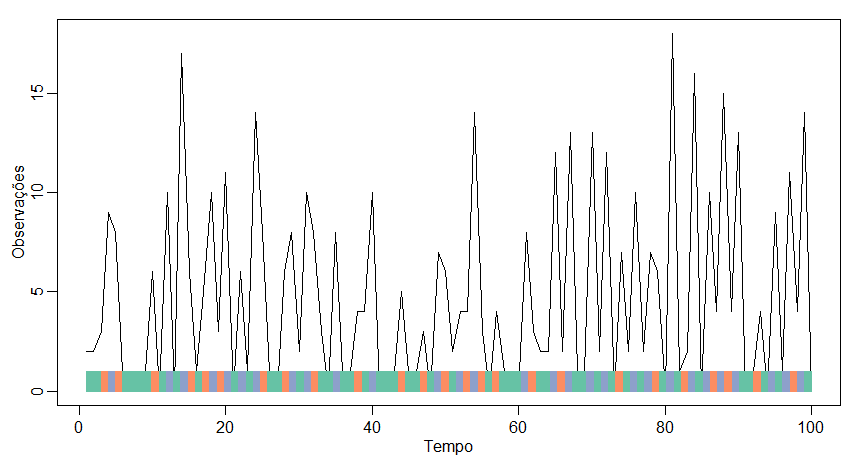
Figura II.5: Dados simulados de um Modelo Oculto de Markov. A barra horizontal mostra os estados diferentes enquanto a curva mostra os valores simulados da distribuição de emissões. As cores correspondem aos estados da seguinte forma: 1=verde, 2=azul e 3=laranja.
Podemos, por exemplo, estimar a matriz de probabilidades de transição da cadeia simulada para verificarmos a qualidade do estimador; ainda obtemos o desvio padrão, os limites inferior e superior do intervalo de confiança de cada elemento da matriz de probabilidades de transição.
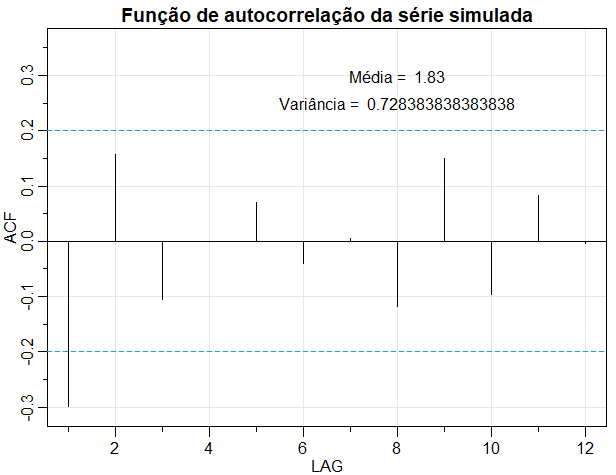
Figura II.1: Função de autocorrelação da série simulada.
Para obter uma primeira compreensão da natureza e propriedades dos HMMs, a simulação de sequências de estados e observações é uma ferramenta útil.
Na seção anterior, a estrutura básica de um HMM e a notação para as distribuições dependentes do estado foram introduzidas. Nesta seção, pretendemos derivar as distribuições marginais de um HMM e os respectivos momentos. Falando em distribuições marginais, entende-se o seguinte: Dado um modelo para \(C_1,\cdots,C_n,S_1,\cdots,S_n\), qual é a distribuição de \(S_t\) ou mesmo a distribuição conjunta de \(S_t\) e \(S_{t+k}\)? Isto é, estamos interessados na distribuição incondicional de \(S_t\), \(P(S_t = s)\), em vez da distribuição condicional \(p_i(s) = P (S_t = s \, | \, C_t = i)\).
Seja \(\{S_t, C_t \, : \, t\in \mathbb{N}\}\) um Modelo Oculto de Markov. Então a distribuição incondicional de \(S_t\) é \begin{equation} P(S_t = s) = \displaystyle \sum_{i=1}^m \delta_i p_i(s), \end{equation} onde \(\delta\) representa a distribuição estacionária da Cadeia de Markov \(C_t\).
Na demonstração acima, o segundo passo decorre do fato de que os estados de \(C_t\) são disjuntos e, portanto, também \(\{S_t = s, C_t = i\}\). A igualdade \(P(C_t = i) = \delta_i\) é uma conseqüência da suposição de que a Cadeia de Markov subjacente é estacionária, o que significa que sua distribuição estacionária \(\delta\) é, para todo \(t\), a distribuição de \(C_t\).
Assim, \(P(S_t = s)\) é simplesmente uma combinação linear das respectivas probabilidades das distribuições de componentes, com a distribuição estacionária \(\delta\) como vetor de pesos.
Usando a notação de matricial, o resultado pode ser reescrito como \begin{equation} P(S_t = s) \, = \, \begin{pmatrix} \delta_1 & \delta_2 & \cdots & \delta_m \end{pmatrix} \begin{pmatrix} p_1(s) & & & 0 \\ & p_2(s) & & \\ & & \ddots & \\ 0 & & & p_m(s) \end{pmatrix} \begin{pmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{pmatrix} \, = \, \delta P(s)\pmb{1}^\top, \end{equation} onde \begin{equation} P(s) \, = \, \begin{pmatrix} p_1(s) & & & 0 \\ & p_2(s) & & \\ & & \ddots & \\ 0 & & & p_m(s) \end{pmatrix}\cdot \end{equation} isto é, uma matriz diagonal contendo as probabilidades da observação \(s\) condicionada nos diferentes estados. Gostaríamos de mencionar novamente, que assumimos que as probabilidades estado-dependentes sejam constantes ao longo do tempo, ou seja, \(P(s)\) vale para todos os \(t\). Caso contrário, seria necessário introduzir um índice de tempo, por exemplo. escreveriamos \(P_t(s)\).
O cálculo da distribuição marginal bivariada de \(S_t\) e \(S_{t+k}\), \(P(S_t = u, S_{t+k} = v)\) é um pouco mais desafiador, mas segue o mesmo procedimento na demonstração do teorema anterior: \begin{array}{rcl} P(S_t=u, \, S_{t+k}=v) & = & \displaystyle \sum_{i=1}^m\sum_{j=1}^m P(S_t=u, \, S_{t+k}=v, \, C_t =i, \, C_{t+k}=j) \\[0.4em] & = & \displaystyle \sum_{i=1}^m\sum_{j=1}^m \underbrace{P(S_t=u, \, S_{t+k}=v, \, | \, C_t =i, \, C_{t+k}=j)}_{\mbox{independência condicional}} P(C_t=i, \, C_{t+k}=j) \\[0.4em] & = & \displaystyle \sum_{i=1}^m\sum_{j=1}^m p_i(u)p_j(v)\underbrace{P(C_t=i)}_{\delta_i}\underbrace{P(C_{t+k}=j \, | \, C_t=i)}_{\gamma_{ij}(k)} \\[0.4em] & = & \displaystyle \sum_{i=1}^m\sum_{j=1}^m \delta_ip_i(u)\gamma_{ij}(k)p_j(v)\cdot \end{array}
Novamente, o resultado pode ser reescrito usando a notação matricial: \begin{equation} P(S_t = u, S_{t+k} = v) \, = \, \delta P(u)\Gamma^k P(v) \pmb{1}^\top, \end{equation} onde \(\delta\), \(\Gamma\) e \(\pmb{1}^\top\) como acima e \begin{equation} P(u) \, = \, \begin{pmatrix} p_1(u) & & & 0 \\ & p_2(u) & & \\ & & \ddots & \\ 0 & & & p_m(u) \end{pmatrix} \qquad \mbox{e} \qquad P(v) \, = \, \begin{pmatrix} p_1(v) & & & 0 \\ & p_2(v) & & \\ & & \ddots & \\ 0 & & & p_m(v) \end{pmatrix}\cdot \end{equation}
O resultado dado na notação matricial pode ser interpretado de uma maneira muito conveniente. As probabilidades iniciais do primeiro estado são dadas por \(\delta\). Portanto, \(\delta\) deve ser multiplicado pela matriz \(P(u)\) que contém as probabilidades da observação \(u\) condicionada aos diferentes estados. Em seguida, multiplicar \(k\) vezes por \(\Gamma\) passa do tempo \(t\) para o tempo \(t + k\). Finalmente, a observação \(v\) é modelada por \(P(v)\) e o vetor unitário, no final, soma as probabilidades.
Seja \(\{S_t, C_t \, : \, t\in \mathbb{N}\}\) um Modelo Oculto de Markov. Então a distribuição marginal multivariada de \(S_t\) é \begin{equation} P(S_t=s, S_{t+k}=u,S_{t+k+l}=v) \, = \, \delta P(s)\Gamma^k P(u) \Gamma^l P(v)\pmb{1}^\top\cdot \end{equation}
Os momentos de um HMM podem ser obtidos de maneira semelhante. Por exemplo, a esperança de \(S_t\), \(\mbox{E}(S_t)\), pode ser rastreada até as esperanças das distribuições de componentes: \begin{equation} \mbox{E}(S_t) \, = \, \sum_{i=1}^m \delta_i \mbox{E}(S_t \, | \, C_t=i)\cdot \end{equation} A prova é direta: \begin{array}{rcl} \mbox{E}(S_t) & = & \displaystyle \sum_s sP(S_t=s) \, = \, \sum_s\sum_{i=1}^m \delta_i p_i(s) \\ & = & \displaystyle \sum_{i=1}^m \delta_i \sum_s sp_i(s) \, = \, \sum_{i=1}^m \delta_i \mbox{E}(S_t \, | \, C_t=i)\cdot \end{array}
Assim, a esperança de \(S_t\), \(\mbox{E}(S_t)\), pode ser interpretada como uma combinação linear das esperanças das distribuições de componentes com \(\delta\) como vetor de pesos. Este resultado pode ser generalizado para qualquer função \(g\) de \(S_t\), \(g(S_t)\) e, portanto, para qualquer momento de ordem superior e então: \begin{equation} \mbox{E}\big(g(S_t)\big) \, = \, \sum_{i=1}^m \delta_i \mbox{E}\big(g(S_t) \, | \, C_t=i \big)\cdot \end{equation} A prova é semelhante à derivação de \(\mbox{E}(S_t)\) e é deixada ao leitor como um exercício.
Também é possível derivar momentos da distribuição conjunta de \(S_t\) e \(S_{t+k}\) de maneira semelhante. Por exemplo, a esperança de uma função da distribuição conjunta \(\mbox{E}\big(g(S_t,S_{t+k})\big)\).
Seja \(\{S_t, C_t \, : \, t\in \mathbb{N}\}\) um Modelo Oculto de Markov. Então a esperança de uma função \(g\) da distribuição conjunta \(\mbox{E}\big(g(S_t,S_{t+k})\big)\) é \begin{equation} \mbox{E}\big(g(S_t,S_{t+k})\big) \, = \, \sum_{i=1}^m \sum_{j=1}^m \delta_i\gamma_{ij}(k)\mbox{E}\big(g(S_t,S_{t+k}) \, | \, C_t=i,C_{t+k}=j\big), \end{equation} onde \(\gamma_{ij}(k)=(\Gamma^k)_{ij}\), é a probabilidade de transição \(k\)-passos do estado \(i\) para o estado \(j\) da Cadeia de Markov subjacente, ou seja, o elemento na \(i\)-ésima linha e \(j\)-ésima coluna da matriz de probabilidade de transição \(k\)-passos \(\Gamma(k)=\Gamma^k\).
Do ponto de vista teórico, também é possível derivar fórmulas para os momentos centralizados, por exemplo, a variância \(\mbox{Var}(S_t)\), mas caso as distribuições reais dos componentes sejam desconhecidas, as fórmulas podem se tornar desagradáveis. Portanto, gostaríamos apenas de mencionar que, em geral, \(\mbox{Var}(S_t)\) pode ser calculado usando \begin{equation} \mbox{Var}(S_t) \, = \, \mbox{E}(S_t^2)-\mbox{E}^2(S_t)\cdot \end{equation}
Usando essa igualdade e a fórmula acima para \(\mbox{E}\big(g(S_t)\big)\), pode-se derivar os seguintes momentos de um processo de Poisson HMM: \begin{array}{rcl} \mbox{E}(S_t) & = & \displaystyle \sum_{i=1}^m \delta_i\lambda_i \, = \, \delta\lambda^\top, \\ \mbox{E}(S_t^2) & = & \displaystyle \sum_{i=1}^m (\lambda_i^2+\lambda_i)\delta_i \, = \, \lambda D\lambda^\top+\delta\lambda^\top, \\ \mbox{Var}(S_t) & = & \displaystyle \sum_{i=1}^m (\lambda_i^2+\lambda_i)\delta_i -\Big(\sum_{i=1}^m \delta_i\lambda_i\Big)^2 \, = \, \lambda D\lambda^\top+\delta\lambda^\top-(\delta\lambda^\top)^2, \\ \mbox{E}(S_tS_{t+k}) & = & \displaystyle \sum_{i=1}^m \sum_{j=1}^m \lambda_i\lambda_j \delta_i \gamma_{ij}(k) \, = \, \delta\Lambda\Gamma^k\lambda^\top, \\ \mbox{Cov}(S_t,S_{t+k}) & = & \displaystyle \sum_{i=1}^m \sum_{j=1}^m \lambda_i\lambda_j \delta_i \gamma_{ij}(k) - \Big( \sum_{i=1}^m \delta_i\lambda_i \Big)^2 \, = \, \delta\Lambda\Gamma^k\lambda^\top - (\delta\lambda^\top)^2, \\ \rho_k \, = \, \mbox{Corr}(S_t,S_{t+k}) & = & \dfrac{\displaystyle \sum_{i=1}^m \sum_{j=1}^m \lambda_i\lambda_j \delta_i \gamma_{ij}(k) - \Big( \sum_{i=1}^m \delta_i\lambda_i \Big)^2} {\displaystyle \sum_{i=1}^m (\lambda_i^2+\lambda_i)\delta_i -\Big(\sum_{i=1}^m \delta_i\lambda_i\Big)^2} \, = \, \dfrac{\delta\Lambda\Gamma^k\lambda^\top - (\delta\lambda^\top)^2}{\delta\Lambda\lambda^\top +\delta\lambda^\top -(\delta\lambda^\top)^2}, \end{array} onde \(\lambda= (\lambda_1,\cdots,\lambda_m)\) é o vetor dos parâmetros da distribuição do processo estado-dependentes de Poisson, \(\delta=(\delta_1,\cdots,\delta_m)\) é a distribuição estacionária da Cadeia de Markov subjacente, \(\Gamma\) é a matriz de probabilidades de transição, \(D = \mbox{diag}(\delta)\) e \(\Lambda=\mbox{diag}(\lambda)\), ou seja, as matrizes diagonais com os elementos de \(\delta\) e \(\lambda\)¸ respectivamente.
Para um processo HMM Poisson de dois estados, os momentos são reduzidos a: \begin{array}{rcl} \mbox{E}(S_t) & = & \displaystyle \delta_1\lambda_1 + \delta_2\lambda_2, \\ \mbox{E}(S_t^2) & = & \displaystyle (\lambda_1+\lambda_1^2)\delta_1 + (\lambda_2+\lambda_2^2)\delta_2, \\ \mbox{Var}(S_t) & = & \displaystyle \delta_1\lambda_1 + \delta_2\lambda_2 + \delta_1\delta_2(\lambda_2-\lambda_1)^2, \\ \mbox{E}(S_tS_{t+k}) & = & \displaystyle \delta_1\delta_2(\lambda_2-\lambda_1)^2(1- \gamma_{12}-\gamma_{21})^k+(\delta_1\lambda_1+\delta_2\lambda_2)^2, \\ \mbox{Cov}(S_t,S_{t+k}) & = & \displaystyle \delta_1\delta_2(\lambda_2-\lambda_1)^2(1-\gamma_{12}-\gamma_{21})^k, \\ \rho_k & = & \dfrac{\displaystyle \delta_1\delta_2(\lambda_1-\lambda_1)^2(1-\gamma_{12}-\gamma_{21})^k} {\displaystyle \delta_1\lambda_1+\delta_2\lambda_2+\delta_1\delta_2(\lambda_1-\lambda_1)^2}\cdot \end{array} A obtenção de algumas dessas expressões não é tão simples quanto parece. Por exemplo, o cálculo de \(\mbox{E}(S_tS_{t+k})\) é bastante complicado, pois é necessário encontrar uma expressão explcíta para \(\gamma_{ij}(k)\) ou \(\Gamma^k\), respectivamente.
O objetivo desta seção é desenvolver uma expressão fechada para a verossimilhança de um HMM em uma estrutura geral. Para motivar o entendimento da verossimilhança, a princípio um exemplo simples é considerado antes que a forma geral da verossimilhança seja derivada.
Obtivemos, no Teorema II.1, uma expressão para a distribuição multivariada de \(S_t\), \(S_{t+k}\) e \(S_{t+k+l}\) como \begin{equation} P(S_t=s,S_{t+k}=u,S_{t+k+l}=v) \, = \, \delta P(s)\Gamma^k P(u)\Gamma^l P(v)\pmb{1}^\top\cdot \end{equation} Por exemplo, alguém pode estar interessado no cálculo da probabilidade de um HMM assumir os valores \(s\) em \(t = 1\), \(u\) em \(t = 3\) e \(v\) em \(t = 7\). De acordo com a expressão acima, essa probabilidade é dada por \begin{equation} P(S_1=s,S_{3}=u,S_{7}=v) \, = \, \delta P(s)\Gamma^2 P(u)\Gamma^4 P(v)\pmb{1}^\top\cdot \end{equation}
Para demonstrar que a fórmula realmente é válida, gostaríamos de considerar um exemplo simples. Por exemplo, considere um HMM Bernoulli de dois estados onde a matriz de probabilidade de transição é a respectiva distribuição estacionária \(\delta\) são dadas por \begin{equation} \Gamma \, = \, \begin{pmatrix} \dfrac{1}{2} & \dfrac{1}{2} \\ \dfrac{1}{4} & \dfrac{3}{4} \end{pmatrix} \qquad \mbox{e} \qquad \delta \, = \, \Big( \dfrac{1}{3},\dfrac{2}{3} \Big)\cdot \end{equation}
As probabilidades dependentes do estado são determinadas por duas variáveis aleatórias com distribuição Bernoulli, em que o primeiro estado representa o caso de jogar uma moeda justa e o segundo caso indica o caso determinístico, ou seja, \begin{array}{rcl} p_1(0) & = & P(S_t=0 \, | \, C_t=1) \, = \, \dfrac{1}{2}, \\ p_1(1) & = & P(S_t=1 \, | \, C_t=1) \, = \, \dfrac{1}{2}, \\ p_2(0) & = & P(S_t=0 \, | \, C_t=2) \, = \, 0 \\ & \mbox{e} & \\ p_2(1) & = & P(S_t=1 \, | \, C_t=2) \, = \,1 \cdot \end{array}
Então, a verossimilhança de \(S_1 = S_2 = S_3 = 1\) pode ser calculada da seguinte maneira: \begin{array}{l} P(S_1 =1, S_2 = 1, S_3 = 1) = \\ \qquad \qquad = \displaystyle\sum_{i=1}^2\sum_{j=1}^2\sum_{k=1}^2 P(S_1 =1, S_2 = 1, S_3 = 1,C_1=i, C_2=j, C_3=k) \\ \qquad \qquad = \displaystyle\sum_{i=1}^2\sum_{j=1}^2\sum_{k=1}^2 P(S_1 =1, S_2 = 1, S_3 = 1 \, | \, C_1=i, C_2=j, C_3=k)\times P(C_1=i, C_2=j, C_3=k) \\ \qquad \qquad = \displaystyle\sum_{i=1}^2\sum_{j=1}^2\sum_{k=1}^2 \underbrace{P(S_1 =1 \, | \, C_1=i)}_{p_i(1)}\underbrace{P(S_2 = 1 \, | \, C_2=j)}_{p_j(1)} \underbrace{P(S_3 = 1 \, | C_3=k)}_{p_k(1)}\times P(C_1=i, C_2=j, C_3=k) \\ \qquad \qquad = \displaystyle\sum_{i=1}^2\sum_{j=1}^2\sum_{k=1}^2 p_i(1)p_j(1)p_k(1)\delta_i\gamma_{ij}\gamma_{jk}\cdot \end{array}
A terceira etapa segue a propriedade de independência condicional do HMM e a última etapa pode ser derivada usando a propriedade de Markov da Cadeia Markov subjacente \(\{C_t\}\): \begin{array}{rcl} P(C_1=i, C_2=j, C_3=k) & = & P(C_1=i)P(C_2=j \, | \, C_1=i)P(C_3=k \, | \, C_1=i, C_2=j) \\ & = & P(C_1=i)P(C_2=j \, | \, C_1=i)P(C_3=k \, | \, C_2=j) \, = \, \delta_i \gamma_{ij}\gamma_{jk}\cdot \end{array}
Agora, para calcular a verossimilança, os possíveis valores de \(i\), \(j\) e \(k\), portanto, de \(\delta_i\), \(\gamma_{ij}\), \(\gamma_{jk}\), \(p_i(1)\), \(p_j(1)\) e \(p_k(1)\) podem ser escritos em uma tabela e a soma acima pode ser obtida multiplicando os valores por linha por e somando os produtos resultantes, conforme demonstrado na tabela a seguir.
| \(i\) | \(j\) | \(k\) | \(p_i(1)\) | \(p_j(1)\) | \(p_k(1)\) | \(\delta_i\) | \(\gamma_{ij}\) | \(\gamma_{jk}\) | \(\prod\) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | \(\frac{1}{2}\) | \(\frac{1}{2}\) | \(\frac{1}{2}\) | \(\frac{1}{3}\) | \(\frac{1}{2}\) | \(\frac{1}{2}\) | \(\frac{1}{96}\) | |||||||||||||||||
| 1 | 1 | 2 | \(\frac{1}{2}\) | \(\frac{1}{2}\) | 1 | \(\frac{1}{3}\) | \(\frac{1}{2}\) | \(\frac{1}{2}\) | \(\frac{1}{48}\) | |||||||||||||||||
| 1 | 2 | 1 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | \(\frac{1}{3}\) | \(\frac{1}{2}\) | \(\frac{1}{4}\) | \(\frac{1}{96}\) | |||||||||||||||||
| 1 | 2 | 2 | \(\frac{1}{2}\) | 1 | 1 | \(\frac{1}{3}\) | \(\frac{1}{2}\) | \(\frac{3}{4}\) | \(\frac{1}{16}\) | |||||||||||||||||
| 2 | 1 | 1 | 1 | \(\frac{1}{2}\) | \(\frac{1}{2}\) | \(\frac{2}{3}\) | \(\frac{1}{4}\) | \(\frac{1}{2}\) | \(\frac{1}{48}\) | |||||||||||||||||
| 2 | 1 | 2 | 1 | \(\frac{1}{2}\) | 1 | \(\frac{2}{3}\) | \(\frac{1}{4}\) | \(\frac{1}{2}\) | \(\frac{1}{24}\) | |||||||||||||||||
| 2 | 2 | 1 | 1 | 1 | \(\frac{1}{2}\) | \(\frac{2}{3}\) | \(\frac{3}{4}\) | \(\frac{1}{4}\) | \(\frac{1}{16}\) | |||||||||||||||||
| 2 | 2 | 2 | 1 | 1 | 1 | \(\frac{2}{3}\) | \(\frac{3}{4}\) | \(\frac{3}{4}\) | \(\frac{3}{8}\) | |||||||||||||||||
| \(\sum\) | \(\frac{29}{48}\) |
Na tabela acima \(\prod\) denota o produto de \(p_i(1)p_j(1)p_k(1)\delta_i\gamma_{ij}\gamma_{jk}\) dados dos valores de \(i\), \(j\) e \(k\) e \(\sum\) denota a soma de todos os produtos. Assim, obtivemos a soma tripla dada acima, ou seja, a verossimilança de \(S_1 = S_2 = S_3 = 1\), a saber \begin{equation} P\big( \{S_1=1, S_2=1, S_3=1\}\big) \, = \, \dfrac{29}{48}\cdot \end{equation}
Também é possível, e ainda mais fácil, calcular a verossimilança usando a notação matricial, pois a soma tripla que gera a verossimilança pode ser reescrita da seguinte maneira: \begin{array}{rcl} P\big( \{S_1=1, S_2=1, S_3=1\}\big) & = & \displaystyle \sum_{i=1}^2\sum_{j=1}^2\sum_{k=1}^2 p_i(1)p_j(1)p_k(1)\delta_i\gamma_{ij}\gamma_{jk} \\ & = & \displaystyle \sum_{i=1}^2\sum_{j=1}^2\sum_{k=1}^2 \delta_ip_i(1)\gamma_{ij}p_j(1)\gamma_{jk}p_k(1) \\ & = & \displaystyle \delta P(1)\Gamma P(1)\Gamma P(1)\pmb{1}^\top \end{array} onde \(\delta\) e \(\Gamma\) são dadas como dado acima e \(P(1)\) é uma matriz diagonal que contém as probabilidades de estado-dependentes \(p_1(1)\) e \(p_2(1)\) com elementos diagonais: \begin{equation} P(1) \, = \, \begin{pmatrix} \frac{1}{2} & 0 \\ 0 & 1 \end{pmatrix}\cdot \end{equation} Isso é exatamente equivalente à fórmula da distribuição multivariada dada acima.
Outro fato interessante nesse contexto é que, embora eles sejam baseados em uma Cadeia de Markov, os HMMs não possuem a propriedade de Markov em geral. Isso pode ser demonstrado com um simples contra-exemplo.
Para o dado HMM Bernoulli, obtém-se que \begin{equation} P\big( \{S_3=1 \, | \, S_1=1, S_2=1\}\big) \, = \, \dfrac{P\big( \{S_1=1, S_2=1, S_3=1\}\big)}{P\big( \{S_1=1, S_2=1\}\big)} \, = \, \dfrac{\frac{29}{48}}{\frac{17}{24}} \, = \, \dfrac{29}{34}, \end{equation} enquanto \begin{equation} P\big( \{S_3=1 \, | \, S_2=1\}\big) \, = \, \dfrac{P\big( \{S_2=1, S_3=1\}\big)}{P\big( \{S_2=1\}\big)} \, = \, \dfrac{\frac{17}{24}}{\frac{5}{6}} \, = \, \dfrac{17}{20}, \end{equation} onde \(P\big( \{S_1=1, S_2=1\}\big)=P\big( \{S_2=1, S_3=1\}\big)\) e \(P\big( \{S_2=1\}\big)\) pode ser obtido construindo uma tabela como a Tabela II.1 ou via multiplicação de matrizes de acordo com \begin{equation} P\big( \{S_1=1, S_2=1\}\big) \, = \, P\big( \{S_2=1, S_3=1\}\big) \, = \, \delta P(1)\Gamma P(1)\pmb{1}^\top \end{equation} e \begin{equation} P\big( \{S_2=1\}\big) \, = \, \delta P(1)\pmb{1}^\top\cdot \end{equation}
Assim, neste caso, \begin{equation} P\big( \{S_3 = 1 \, | \, S_2 = 1\} \big) \, \neq \, P\big( \{S_3=1 \, | \, S_1=1, S_2=1\}\big), \end{equation} ou seja, o HMM considerado aqui não possui a propriedade de Markov. Para as condições sob as quais um HMM irá satisfazer a propriedade Markov, consulte Spreij (2001).
Agora voltamos ao objetivo desta seção, ou seja, a derivação de uma expressão fechada para a verossimilhança de um HMM em geral. Analogamente ao exemplo acima e à fórmula para a distribuição marginal multivariada, obtém-se a seguinte expressão para a verossimilança \(L_T\) de um HMM.
Seja \(\{S_t, C_t \, : \, t\in \mathbb{N}\}\) um Modelo Oculto de Markov. A função de verossimilança assume a forma \begin{equation} L_T \, = \, P(\{S_1 = s_1, S_2=s_2, \cdots, S_T=s_T) = \displaystyle \delta P(s_1)\Gamma P(s_2)\Gamma \cdots \Gamma P(s_T)\pmb{1}^\top\cdot \end{equation}
A primeira parte da terceira etapa da demonstração segue da propriedade de indepenêência condicional dos HMMs, enquanto a segunda parte da etapa três pode ser derivada da propriedade Markov da cadeia subjacente de Markov.
Agora, usando a igualdade \(\delta=\delta\Gamma\) e definindo \(B_t =\Gamma P(s_t)\) para todos os \(t\in\{1,2,\cdots,T\}\), a verossimilança pode ser reescrita de uma forma mais conveniente: \begin{equation} L_T \, = \, \delta B_1 B_2 \cdots B_T\pmb{1}^\top\cdot \end{equation}
Uma propriedade extremamente agradável dos HMMs é a facilidade com que se pode lidar com as observações ausentes. Suponha, por exemplo, que se tenham observado as realizações \(s_1, s_2, s_4, s_7,\cdots, s_T\) apenas de um HMM, isto é, as realizações \(s_3, s_5\) e \(s_6\) estão ausentes. Então, para calcular a verossimilança das observações dadas é necessário substituir apenas as respectivas matrizes diagonais que contêm as probabilidades estado-dependentes das observações ausentes, isto é, \(P(s_3)\), \(P(s_5)\) e \(P(s_6)\) por uma matriz unitária \(\mbox{I}\) na fórmula acima da verossimilança e obtém-se: \begin{array}{rcl} L_T^{-(3,5,6)} & = & P(S_1=s_1, S_2=s_2, S_4=s_4, S_7=s_7,\cdots,S_T=s_T) \\[0.4em] & = & \delta P(s_1)\Gamma P(s_2)\Gamma \, \mbox{I} \,\Gamma P(s_4)\Gamma \, \mbox{I} \, \Gamma \, \mbox{I} \, \Gamma P(s_7)\cdots \Gamma P(s_T)\pmb{1}^\top \\[0.4em] & = & \delta P(s_1)\Gamma P(s_2)\Gamma^2 P(s_4)\Gamma^3 P(s_7)\cdots \Gamma P(s_T)\pmb{1}^\top, \end{array} onde as observações ausentes são indicadas por um índice superior adicional.
Observe que essa verossimilança não passa de uma distribuição marginal multivariada de \(S_1, S_2, S_4, S_7, \cdots, S_T\), avaliada nas observações \(s_1, s_2, s_4, s_7, \cdots, s_T\). Novamente, a verossimilança pode ser reescrita usando \(B_t=\Gamma P(s_t)\): \begin{equation} L_T^{-(3,5,6)} \, = \, \delta B_1 B_2 \Gamma B_4 \Gamma^2 B_7 \cdots B_T\pmb{1}^\top\cdot \end{equation} O fato de que, mesmo no caso de observações ausentes, a verossimilança de um HMM pode ser facilmente calculada é especialmente útil para a derivação de distribuições condicionais, como será mostrado na Seção IV.1.
Em um contexto de séries temporais, é potencialmente estranho se alguns dados estiverem ausentes. No caso de Modelos Ocultos de Markov de séries temporais, no entanto, o ajuste que precisa ser feito no cálculo da verossimilhança, se houver dados ausentes, acaba sendo simples.
Suponha, por exemplo, que se tenham disponíveis as observações \(s_1,s_2,s_4,s_7,s_8,\cdots,s_T\) de um HMM, mas as observações \(s_3,s_5\) e \(s_6\) estejam ausentes aleatoriamente.
A verossimilhança é dada por \begin{equation} P(S_1=s_1, S_2=s_2, S_4=s_4, S_7=s_7,\cdots,S_T=s_T) \, = \, \qquad \qquad \qquad \qquad \qquad\qquad\qquad\qquad\qquad\qquad \\ \qquad \qquad \displaystyle = \, \sum \delta_{c_1}\gamma_{{c_1,c_2}}\gamma_{{c_2,c_4}}(2)\gamma_{{c_4,c_7}}(3)\gamma_{{c_7,c_8}}\cdots \gamma_{{c_{T-1},c_T}}(2)\times p_{c_1}(s_1)p_{c_2}(s_2)p_{c_4}(s_4)p_{c_7}(s_7)\cdots p_{c_T}(s_T), \end{equation} onde, como antes, \(\gamma_{ij}(k)\) denota a probabilidade de transição em \(k\)-passos e a soma é tomada sobre todos os \(c_t\) exceto \(c_3, c_5\) e \(c_6\). Mas isso é justamente \begin{equation} \displaystyle \sum \delta_{c_1}p_{c_1}(s_1)\gamma_{{c_1,c_2}}p_{c_2}(s_2)\gamma_{{c_2,c_4}}(2)p_{c_4}(s_4)\gamma_{{c_4,c_7}}(3)p_{c_7}(s_7) \cdots \gamma_{{c_{T-1},c_T}} p_{c_T}(s_T) \, = \qquad\qquad\qquad\qquad \\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad = \, \delta P(s_1)\Gamma P(s_2)\Gamma^2 P(s_4)\Gamma^3 P(s_7)\cdots \Gamma P(s_T)\pmb{1}^\top\cdot \end{equation}
Denotando por \(L_T^{-(3,5,6)}\) a verossimilhança das observações diferentes de \(s_3, s_5\) e \(s_6\), nossa conclusão é, portanto, que \begin{equation} L_T^{-(3,5,6)} \, = \, \delta P(s_1)\Gamma P(s_2)\Gamma^2 P(s_4)\Gamma^3 P(s_7)\cdots \Gamma P(s_T)\pmb{1}^\top\cdot \end{equation}
A maneira mais fácil de resumir essa conclusão é dizer que, na expressão da verossimilhança, as matrizes diagonais \(P(s_t)\) correspondentes às observações ausentes \(s_t\) são substituídas pela matriz identidade; de maneira equivalente, as distribuições de estado-dependentes \(p_i(s_t)\) são substituídas por 1 para todos os estados \(i\).
O fato de que, mesmo no caso de observações ausentes, a verossimilhança de um HMM pode ser calculada é especialmente útil na derivação de distribuições condicionais, como também é mostrado na Seção IV.1
Suponha que desejemos ajustar um Poisson-HMM a uma série de contagens, algumas das quais são censuradas por intervalo. Por exemplo, o valor exato de \(s_t\) pode ser conhecido apenas por \(4\leq t \leq T\), com as informações \(s_1\leq 5, 2\leq s_2\leq 3\) e \(s_3 > 10\), disponíveis sobre as observações restantes.
Por uma questão de simplicidade, vamos primeiro assumir que a Cadeia de Markov possui apenas dois estados. Nesse caso, substitua-se a matriz diagonal \(P(s_1)\) na expressão da verossimilhança pela matriz \begin{equation} \mbox{diag}\big( P(S_1\leq 5 \, | \, C_1=1), P(S_1\leq 5 \, | \, C_1=2)\big), \end{equation} e da mesma forma para \(P(s_2)\) e \(P(s_3)\).
De maneira mais geral, suponha que \(a\leq s_t\leq b\), onde \(a\) possa ser \(-\infty\), embora isso não seja relevante para o caso Poisson, \(b\) possa ser \(\infty\) e a Cadeia de Markov tenha \(m\) estados. Substitui-se \(P(s_t)\) na verossimilhança pela matriz \(m \times m\) diagonal da qual o \(i\)-ésimo elemento diagonal é \begin{equation} P(a\leq S_t \leq b \, | \, C_t=i)\cdot \end{equation}
Obtenha os seguintes resultados para os momentos do HMM.
Obtenha os seguintes resultados para os momentos do HMM.