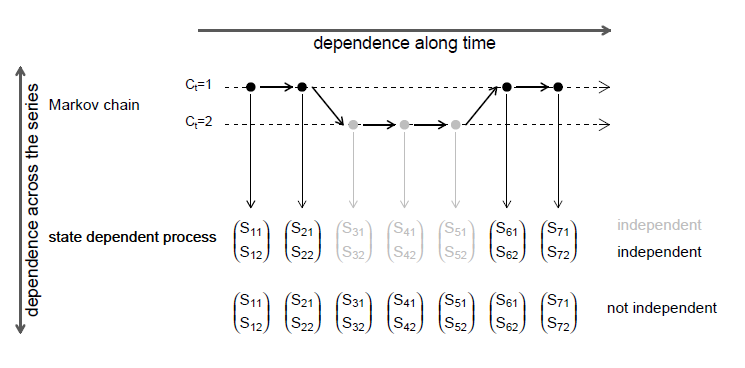
Figura VI.1: A independência condicional contemporânea.
Uma das principais vantagens dos HMMs é a facilidade com que o modelo básico pode ser generalizado, de várias maneiras diferentes, para fornecer modelos para uma ampla gama de séries temporais. Aqui descrevemos a aplicação do HMM básico usando outras distribuições de componentes que não o Poisson (Seção VI.1) e as idéias básicas de algumas possíveis extensões do HMM básico (Seções VI.2 a VI.4).
A primeira generalização que discutiremos na Seção VI.2 adiciona flexibilidade ao modelo básico generalizando o processo de parâmetro subjacente. A suposição de que o processo de parâmetro é uma Cadeia de Markov de primeira ordem é relaxada, permitindo que esta seja uma Cadeia de Markov de segunda ordem. Essa extensão pode ser aplicada não apenas ao modelo básico, mas também à maioria dos outros modelos a serem discutidos.
Ilustraremos como o modelo básico pode ser generalizado para construir HMMs para vários tipos diferentes e mais complexos de séries temporais, incluindo o seguinte.
Exemplos de séries do tipo multinomial incluem vendas diárias de um item específico categorizado nas quatro categorias de consumidor: fêmea adulta, macho adulto, fêmea juvenil, macho juvenil. Um caso especial importante da série multinomial é aquele em que há exatamente um dos \(q\) possíveis resultados mutuamente exclusivos em cada período, que é uma série temporal categórica. Um exemplo é uma série temporal de direções horárias do vento na forma das 16 categorias convencionais, isto é, os 16 pontos da bússola.
Um exemplo de uma série de valores discretos bivariados é o número de vendas de cada um dos dois itens relacionados. Um recurso importante das séries temporais multivariadas é que, além da dependência serial dentro de cada série, pode haver dependência entre as séries.
Muitas, senão a maioria, séries temporais estudadas na prática exibem tendência, variação sazonal ou ambas. Exemplos incluem vendas mensais de itens, número diário de ações negociadas, reclamações de seguros recebidas e assim por diante. Pode-se considerar essas séries como dependendo da covariada tempo. Em alguns casos, covariáveis diferentes do tempo são relevantes. Por exemplo, pode-se querer modelar o número de vendas de um item em função do preço, gastos com publicidade, vendas, promoções e permitir tendências e flutuações sazonais.
Observe que esta parte, ou pelo menos as Seções VI.2 a VI.4, não faz parte da introdução geral ao HMM básico, mas serve para uma leitura mais aprofundada. Por esse motivo, nos concentramos em delinear as idéias básicas das possíveis extensões e aplicativos possíveis, sem fornecer todos os detalhes. Para uma descrição mais detalhada dessas extensões e suas aplicações, especialmente para variáveis aleatórias discretas, nos referimos a MacDonald and Zucchini (1997).
Neste artigo, introduzimos o HMM básico concentrado nas distribuições de componentes de Poisson. No entanto, como já mencionado, pode-se usar qualquer outra distribuição discreta ou contínua possível para modelar as distribuições dependentes do estado, na verdade, é até possível usar distribuições diferentes para estados diferentes. Basta redefinir as matrizes que contêm as probabilidades dependentes do estado e, eventualmente, as transformações dos parâmetros dependentes do estado no processo de estimação.
A seguir, descrevemos algumas aplicações possíveis de HMMs com várias distribuições de componentes sem entrar em detalhes, para obter mais detalhes sobre HMMs com outras distribuições de componentes de valor discreto que o Poisson e suas aplicações, respectivamente, nos referimos a MacDonald and Zucchini (1997).
A distribuição de Poisson é o modelo clássico para contagens ilimitadas. No entanto, uma alternativa popular para modelar contagens ilimitadas, especialmente para dados super dispersos, é a distribuição Binomial Negativa, cujas probabilidades dependentes do estado são dadas por \begin{equation} p_i(s) \, = \, \dfrac{\Gamma\Big(s+\frac{1}{\eta_i}\Big)}{\Gamma\Big(\frac{1}{\eta_i}\Big)\Gamma(x+1)}\left( \dfrac{1}{1+\eta_i\mu_i}\right)^{\frac{1}{\eta_i}}\left( \dfrac{\eta_i\mu_i}{1+\eta_i\mu_i}\right)^{x}, \qquad s=0,1,2,,\cdots, \end{equation} com \(\mbox{E}(S_t|C_t=i)=\mu_i\) e \(\mbox{Var}(S_t|C_t=i)=\mu_i(1+\eta_i\mu_i)\).
Observe que esta é apenas uma das várias parametrizações possíveis da distribuição Binomial Negativa. Um HMM Binomial Negativo pode ser aplicado caso os dados ainda sejam superdispersos em relação a um HMM Poisson. Exemplos econômicos concebíveis para a aplicação de HMMs Poisson ou Binomiais Negativos incluem uma série de contagens de paradas ou avarias de equipamentos técnicos, terremotos, vendas (consulte a série de vendas de sabonetes), reclamações de seguros, acidentes relatados, itens defeituosos ou operações com ações.
O HMM Bernoulli pode ser usado para modelar séries temporais binárias é o HMM mais simples. Suas probabilidades dependentes do estado para os dois resultados possíveis são dadas por \begin{array}{rcl} p_i(0) & = & P(S_t=0 \, | \, C_t=i) \, = \, 1-\pi_i \qquad (fracasso), \\ p_I(1) & = & P(S_t=1 \, | \, C_t=i) \, = \, \pi_i \quad \quad \quad \, \, \, \, (sucesso)\cdot \end{array}
Os HMMs binomiais podem ser aplicados a séries de modelos de contagens limitadas em que \(n_t\) é o número de tentativas no tempo \(t\) e \(s_t\) é o número de sucessos no tempo \(t\). As probabilidades binomiais dependentes do estado são dadas por \begin{equation} p_{_{t_i}}(s) \, = \, \binom{n_t}{s_t}\pi_i^{s_t}(1-\pi_i)^{n_t-s_t}\cdot \end{equation}
Exemplos possíveis para séries de contagens limitadas que podem ser descritas por um HMM binomial são séries de
Observe que há uma restrição ao calcular a distribuição de previsão de um HMM Binomial. O número de tentativas no momento \(T + h\) deve ser conhecido ou é necessário ajustar um modelo separado para prever o número respectivo de tentativas. Obviamente, configurando \(n_{T + h} = 1\), também é possível simplesmente calcular a distribuição prevista das proporções de contagem.
Até o momento, consideramos principalmente os HMMs com distribuições de componentes dependentes do estado com valores discretos. No entanto, também mencionamos que é possível usar distribuições de componentes com valor contínuo. Basta substituir as funções de probabilidade pelas respectivas funções de densidade dependentes do estado.
HMMs importantes para séries temporais de valor contínuo são HMMs exponenciais, gama ou normais. Observe que a verosossimilhança de um HMM normal é realmente ilimitada; teoricamente, é possível aumentar a verosossimilhança infinitamente, deixando que uma variação dependente do estado, \(\sigma_i\), se aproxime de zero. Na prática, isso pode estar relacionado a problemas na estimação de parâmetros.
Uma generalização do modelo HMM básico é um HMM de segunda ordem. Isso pode ser construído substituindo a Cadeia de Markov de primeira ordem subjacente no modelo básico ou nas extensões a seguir por uma cadeia de segunda ordem estacionária. Este último é caracterizado pelas probabilidades de transição \begin{equation} \gamma_{ijk} \, = \, P(C_t=k \, | \, C_{t-1}=j, C_{t-2}=i) \end{equation} e a distribuição bivariada estacionária \(u(j,k) = P(C_{t-1} = j, C_t = k)\). Ou seja, as probabilidades \(u(j,k)\) satisfazem \begin{equation} u(j,k) \, = \, \sum_{i=1}^m u(i,j)\gamma_{ijk} \qquad \mbox{e} \qquad \sum_{j=1}^m\sum_{k=1}^m u(j,k) \, = \, 1\cdot \end{equation}
O processo \(\{C_t\}\) não é uma Cadeia de Markov de primeira ordem, mas podemos definir um novo processo \(\{X_t\}\) com \(X_t = (C_{t-1}, C_t)\), que é uma Cadeia de Markov de primeira ordem, no espaço de estados \(M^2\). Por exemplo, considere a Cadeia de Markov estacionária mais geral de segunda ordem \(\{C_t\}\) nos dois estados 1 e 2. Isso pode ser caracterizado pelas quatro probabilidades de transição: \begin{array}{rcl} a \, = \, P(C_t=2 \, | \, C_{t-1}=1, C_{t-2}=1), & \qquad & b \, = \, P(C_t=1 \, | \, C_{t-1}=2, C_{t-2}=2), \\ c \, = \, P(C_t=1 \, | \, C_{t-1}=2, C_{t-2}=1), & \qquad & d \, = \, P(C_t=2 \, | \, C_{t-1}=1, C_{t-2}=2)\cdot \end{array}
O processo \(\{X_t\}\), como definido acima, é então uma Cadeia de Markov de primeira ordem, nos quatro estados (1,1), (1,2), (2,1), (2,2) (em ordem) e com matriz de probabilidade de transição: \begin{equation} \begin{pmatrix} 1-a & a & 0 & 0 \\ 0 & 0 & c & 1-c \\ 1-d & d & 0 & 0 \\ 0 & 0 & b & 1-b \end{pmatrix}\cdot \end{equation} Os parâmetros a, b, c e d são delimitados por 0 e 1, mas são irrestritos. A distribuição estacionária de \(\{X_t\}\) é proporcional a \begin{equation} \begin{pmatrix} b(1-d), & ab & ab, & a(1-c) \end{pmatrix}, \end{equation} daí resulta que a matriz de probabilidades bivariadas estacionárias para \(\{C_t\}\) é \begin{equation} \dfrac{1}{b(1-d)+2ab+a(1-c)}\begin{pmatrix} b(1-d) & ab \\ ab & a(1-c)\end{pmatrix}\cdot \end{equation}
Mencionaremos apenas dois aspectos importantes deste Modelo Oculto de Markov de segunda ordem aqui. Detalhes adicionais são fornecidos na Seção 3.2 de MacDonald and Zucchini (1997).
A primeira é que é possível avaliar a verosossimilhança de um Modelo Oculto de Markov de segunda ordem de maneira muito semelhante à do modelo básico: o esforço computacional é neste caso cúbico em \(m\), o número de estados e, como antes, linear em \(T\), o número de observaçõções. Isso permite estimar os parâmetros, por exemplo, por maximização direta da verossimilhança e também calcular as distribuições previstas.
O segundo aspecto refere-se ao número de parâmetros de componentes do modelo da Cadeia Markov de segunda ordem. Em geral, isso possui \(m^2(m-1)\) parâmetros livres, um número que rapidamente se torna proibitivamente grande à medida que \(m\) aumenta. Esse problema de parametrização excessiva pode ser contornado usando uma subclasse restrita de modelos da Cadeia de Markov de segunda ordem, por exemplo, o descrito por Pegram (1980), que possui apenas \(m+1\) parâmetros ou o descrito por Raftery (1985), que possui \(m(m-1)+1\) parâmetros. Tais modelos são necessariamente menos flexíveis do que a classe geral de Cadeias de Markov de segunda ordem. Eles mantêm a estrutura de segunda ordem da cadeia, mas trocam alguma flexibilidade em troca de uma redução no número de parâmetros.
Tendo apontado que é possível aumentar a ordem da Cadeia de Markov em um HMM de um para dois ou mais, de fato, a seguir, restringiremos nossa atenção ao caso mais simples de uma Cadeia de Markov de primeira ordem.
Um dos exemplos do modelo básico que mencionamos na Seção VI.1 é o HMM Binomial no qual a série de observações \(\{s_t \, : \, t = 1,\cdots,T\}\) pode ser considerado como o número de sucessos em ensaios independentes de Bernoulli. O modelo de \(m\) estados possui probabilidades diferentes de sucesso, \(\pi_i\), uma para cada estado, \(i\). A probabilidade que é aplicável em um determinado momento \(t\) é determinada por uma Cadeia de Markov de primeira ordem \(\{C_t\}\). Assim, por exemplo, se \(C_1 = 2\) e \(C_2 = 4\), a probabilidade de sucesso \(\pi_2\) é aplicável no tempo \(t = 1\) e \(\pi_4\) no tempo \(t = 2\).
Um HMM multinomial é uma generalização do HMM Binomial no qual existem \(q\) resultados possíveis mutuamente exclusivos em cada tentativa, onde \(q\geq 2\). As observações são então \(q\) séries de contagens, \begin{equation} \{s_{tj} \, : \, t = 1,\cdots,T; j = 1,\cdots,q\} \end{equation} com \(s_{t1} + s_{t2}+\cdots+s_{tq} = n_t\) onde \(n_t\) é o número (conhecido) de tentativas no tempo \(t\). Assim, por exemplo, \(s_{23}\) representa o número de resultados no tempo \(t = 2\) que eram do tipo 3. As contagens \(s_{tj}\) no tempo \(t\) podem ser combinadas em um vetor \(s_t = (s_{t1},s_{t2},\cdots,s_{tq}\). Vamos supor que, condicional em \(C^{(T)}\), os \(T\) vetores aleatórios \(\{S_t = (S_{t1},S_{t2},\cdots,S_{tq}) \, : \, t = 1,\cdots,T\}\) são mutuamente independentes.
Os parâmetros do modelo são os seguintes. Como no modelo básico, a matriz \(\Gamma\) possui \(m(m-1)\) parâmetros livres. Com cada um dos \(m\) estados da Cadeia de Markov está associada uma distribuição multinomial com parâmetros \(n_t\) (conhecidos) e \(q\) probabilidades desconhecidas que, para o estado \(i\), denotaremos por \(\pi_{i1},\pi_{i2},\cdots,\pi_{iq}\). Essas probabilidades são restritas porque \begin{equation} \sum_{j=1}^q \pi_{ij} \, = \, 1 \end{equation} para cada estado \(i\). Portanto, este componente do modelo possui \(m(q-1)\) parâmetros livres e o modelo inteiro tem \(m^2-m+(q-1)m = m^2 + m(q-2)\).
A verossimilhança de observações \(s_1,\cdots,s_T\) de um HMM Multinomial geral difere pouco do caso de um HMM Binomial; a única diferença é que as probabilidades binomiais \begin{equation} p_{ti}(s_t) \, = \, \binom{n_t}{s_t}\pi_i^{s_t}(1-\pi_i)^{n_t-s_t} \end{equation} são substituídas pelas probabilidades multinomiais \begin{equation} p_{ti}(s_t) \, = \, P(S_t=s_t \, | \, C_t=i) \, = \, \binom{n_t}{s_{t1},s_{t2},\cdots,s_{tq}}\pi_{i1}^{s_{t1}}\pi_{i2}^{s_{t2}}\cdots\pi_{iq}^{s_{tq}}\cdot \end{equation} Observe que essas probabilidades precisam ser indexadas pelo tempo \(t\), pois o número de tentativas \(n_t\) é dependente do tempo. Por outro lado, assumimos que as probabilidades dependentes do estado \(\pi_{i1},\pi_{i2},\cdots,\pi_{iq}\) sejam constantes ao longo do tempo.
A verossimilhança é, portanto, dada por \begin{equation} L_T \, = \, \delta P_1(s_1)\, \Gamma P_2(s_2)\cdots \Gamma P_T(s_T)\pmb{1}^\top, \end{equation} onde \(P_t(s_t)=\mbox{dias}\big( p_{t1}(s_t),\cdots,p_{tm}(s_t)\big)\).
Ao maximizar a verossimilhança, a fim de estimar parâmetros, deve-se observar uma série de restrições com limite superior generalizado, a saber: \begin{equation} \sum_{j\neq i} \gamma_{ij}\leq 1 \qquad \mbox{e} \qquad \sum_{j=1}^{q-1} \pi_{ij}\leq 1, \end{equation} \(i = 1,2,\cdots,m\), bem como as restrições usuais sobre probabilidades: \(0\leq \gamma_{ij}\leq 1\) e \(0\leq \pi_{ij}\leq 1\).
Uma vez que os parâmetros foram estimados, eles podem ser usados para estimar várias distribuições de previsões, ou seja, as distribuições de valores futuros da série. Isso é feito usando as fórmulas fornecidas para o modelo básico, exceto que as probabilidades dependentes do estado agora são baseadas na distribuição Multinomial e não na Binomial ou Poisson.
Há, no entanto, uma restrição a essas previsões que também se aplica ao HMM Binomial. Assumimos que \(n_t\), o número de tentativas no tempo \(t\), é conhecido. Esse número, sendo a soma das \(q\) observadas no tempo \(t\), é certamente conhecido nos momentos \(t = 1,2,\cdots,T\). Agora, para calcular a distribuição da previsão um passo à frente, é necessário conhecer \(n_{T+1}\), o número de tentativas que ocorrerão no momento \(T + 1\). Isso será conhecido em algumas aplicações, por exemplo, quando o número dos ensaios é prescrito por um esquema de amostragem. No entanto, também existem aplicações em que \(n_{T+1}\) é uma variável aleatória cujo valor permanece desconhecido até o tempo \(T +1\). Assim, para este último, não é possível diretamente calcular a distribuição prevista das contagens no tempo \(T +1\). No entanto, configurando \(n_{T + 1} = 1\), é possível calcular a distribuição prevista das proporções de contagem.
Uma abordagem alternativa, discutida na Seção 3.8 de MacDonald and Zucchini (1997), é ajustar um modelo separado para a série \(\{n_t\}\), usar esse modelo para calcular a distribuição prevista de \(n_{T+1}\) e, finalmente, usá-la para calcular a distribuição de previsão necessária pelas contagens do HMM Multinomial.
Um caso especial simples, mas importante, de Modelos Ocultos de Markov Multinomiais é onde \(n_t = 1\) para todos os \(t\). Isso fornece modelos para séries temporais categóricas. Aqui, as probabilidades dependentes do estado \(p_{t_i}(s_t)\) e a expressão matricial para a verosossimilhança simplificam-se consideravelmente. Se o \(j\)-ésimo componente de \(s_t\) é 1 e os outros são, portanto, 0, temos \begin{equation} p_{t_i}(s_t) \, = \, \pi_{ij}, \end{equation} e o índice \(t\) é desnecessário. Segue que \begin{equation} P(s_t) \, = \, \mbox{diag}\big( p_{t1}(s_t),\cdots,p_{tm}(s_t)\big) \, = \, \mbox{diag}\big(\pi_{1j},\cdots,\pi_{mj} \big) \, = \, P(j_t), \end{equation} se novamente \(s_t\) é um vetor com \(j\)-ésimo componente 1 e os outros 0. Portanto, a verossimilhança de observar as categorias \(j_1,j_2,\cdots,j_T\) às vezes \(1,2,\cdots,T\) é dado por \begin{equation} L_T \, = \, \delta P(j_1) \, \Gamma P(j_2) \, \Gamma \cdots P(j_T)\pmb{1}^\top\cdot \end{equation}
Isso implica, por exemplo, que a probabilidade de observar a categoria \(j\) no tempo \(t\), dado que a categoria \(l\) é observada no tempo \(t-1\), é \begin{equation} \dfrac{\delta P(l) \,\Gamma P(j)\pmb{1}^\top}{\delta P(l)\pmb{1}^\top}\cdot \end{equation} Assim, uma vez que os parâmetros do modelo foram estimados, é fácil calcular a distribuição da previsão.
As séries de contagens multinomiais discutidas na última seção são, obviamente, exemplos de séries multivariadas, mas elas têm uma estrutura específica. Nesta seção, ilustramos como é possível desenvolver HMMs para tipos diferentes e mais complexos de séries multivariadas.
Considere \(q\) séries temporais \(\{(S_{t1},S_{t2},\cdots,S_{tq}) \, : \, t = 1,\cdots,T\}\) que iremos representar compactamente como \(\{S_t \, : \, t = 1,\cdots,T\}\). Como fizemos no HMM básico, assumiremos que, condicional em \(C^{(T)} = \{C_t \, : \, t = 1,\cdots,T\}\), os vetores aleatórios acima são mutuamente independentes. Iremos nos referir a essa propriedade como independência condicional ao longo do tempo, a fim de distingui-la de um tipo diferente de independência condicional que descreveremos mais adiante.
Para especificar um HMM para essa série, é necessário postular um modelo para a distribuição desse vetor aleatório para cada um dos \(m\) estados do processo de parâmetros. Expresso em símbolos, é necessário formular expressões para as probabilidades \begin{equation} p_{ti}(s_t) \, = \, P(S_t = s_t \, | \, C_t = i), \qquad i=1,2,\cdots,m\cdot \end{equation} Por generalidade, mantemos o índice de tempo aqui, ou seja, permitimos que as probabilidades dependentes do estado sejam alteradas ao longo do tempo.
No caso dos HMMs multinomiais, essas probabilidades foram fornecidas por \(m\) distribuições multinomiais. Observamos que não é necessário que cada uma das séries de \(q\) componentes tenha a mesma distribuição. Por exemplo, \(S_{t1}\) pode ser modelado usando uma distribuição Poisson, \(S_{t2}\) usando uma distribuição Bernoulli e assim por diante. A expressão para a verossimilhança fornecida abaixo também se aplica se algumas das séries tiverem valor contínuo.
Em segundo lugar, não é necessário que a distribuição de \(S_{t1}\), digamos, seja do mesmo tipo para cada um dos \(m\) estados da Cadeia de Markov subjacente. Em princípio, pode-se usar a distribuição de Poisson no estado 1, a distribuição Binomial Negativa no estado 2 e assim por diante. Contudo, não encontramos aplicações em que esta característica possa ser explorada de forma útil.
O que é necessário é especificar modelos para \(m\) distribuições conjuntas, uma tarefa que pode ser tudo menos trivial. Por exemplo, não existe uma única distribuição bivariada Poisson; versões diferentes estão disponío;veis e têm propriedades diferentes, em contraste, pode-se razoavelmente falar da distribuição normal bivariada porque, para fins práticos, existe apenas uma. É preciso selecionar uma versão que seja apropriada no contexto da aplicação particular que está sendo investigada.
Uma vez selecionadas as distribuições conjuntas necessárias, ou seja, uma vez dadas as fórmulas para as probabilidades dependentes do estado \(p_{_{ti}}(s_t)\), a verossimilhança de um HMM multivariado geral pode ser escrita. Ela tem essencialmente a mesma forma que o modelo básico, a saber \begin{equation} L_T \, = \, \delta P_1(s_1)\, \Gamma P_2(s_2)\cdots \Gamma P_T(s_T)\pmb{1}^\top, \end{equation} onde \(s_1,\cdots,s_T\) são as observações e \(P_t(s_t) = \mbox{diag}\big(p_{_{t1}}(s_t),\cdots,p_{_{tm}}(s_t)\big)\).
Esta é, na verdade, a mesma fórmula dada acima para séries multinomiais. A tarefa de encontrar distribuições conjuntas adequadas é muito simplificada se for possível fazer a suposição de independência condicional contemporânea.
Vamos ilustrar o significado deste termo através do modelo de precipitação multissítios discutido por Zucchini and Guttorp (1991). Em sua aplicação, há cinco séries temporais binárias representando a presença ou ausência de chuva em cada um dos cinco locais que são considerados ligados por um processo climático comum \(\{C_t\}\). Aí as variáveis aleatórias \(S_{tj}\) são binárias. Seja \(p_{tij}\) definido como \begin{equation} \pi_{tij} \, = \, P(S_{ij}=1 \, | \, C_t=i) \, = \, 1- P(S_{ij}=0 \, | \, C_t=i)\cdot \end{equation}
A hipótese de independência condicional contemporânea implica que a probabilidade conjunta exigida \(p_{_{ti}}(s_t)\) pode ser computada como o produto das probabilidades marginais: \begin{equation} p_{_{ti}}(s_t) \, = \, \prod_{j=1}^q \pi_{tij}^{s_{ij}}\big(1-\pi_{tij}\big)^{1-s_{ij}}\cdot \end{equation}
Assim, por exemplo, dado o estado climático \(i\), a probabilidade de que chova em, digamos, locais \((1,2,4)\) mas não em locais \((3,5)\) no dia \(t\) é o produto das probabilidades marginais de que estes eventos ocorrem, nomeadamente \(\pi_{ti1}\pi_{ii2}(1-\pi_{ti3})\pi_{ti4}(1-\pi_{ti5})\).
Para HMMs multivariados gerais que são contemporaneamente condicionalmente independentes, as probabilidades dependentes do estado são dadas por um produto das \(q\) probabilidades marginais correspondentes: \begin{equation} p_{ti}(s_t) \, = \, \prod_{j=1}^q P\big(S_{tj}=s_{tj} \, | \, C_t=i\big)\cdot \end{equation}
Queremos enfatizar que os dois pressupostos de independência condicional acima mencionados, a saber independência condicional ao longo do tempo e da independência condicional contemporânea, não implica que

Figura VI.1: A independência condicional contemporânea.
Os detalhes relativos às funções de correlação serial e cruzada desses modelos são apresentados na Seção 3.4 de MacDonald and Zucchini (1997), assim como outras classes gerais de modelos para HMMs multivariados, tais como modelos com desfasamentos temporais e modelos em que algumas das variáveis são discretas e outras são contínuas.
Os HMMs multivariados, com distribuições de componentes contínuas podem, por exemplo, ser usados para modelar séries temporais financeiras multivariadas. Por exemplo, pode-se ajustar um HMM normal multivariado de dois estados a uma série multivariada de retornos diários sobre um número de ações onde, como no caso univariado, os estados subjacentes à mudança de Markov podem corresponder para acalmar e turbulentar as fases do mercado bolsista.
Os HMMs também podem ser modificados para permitir a influência dos covariáveis postulando a dependência das probabilidades \(p_{ti}(s_t)\) dependentes do estado sobre esses covariáveis, como demonstrado na Figura VI.2. Isto abre o caminho para que tais modelos incorporem a tendência temporal e a sazonalidade, por exemplo. Na verdade, já permitimos que as probabilidades dependentes do estado mudassem ao longo do tempo na seção anterior.
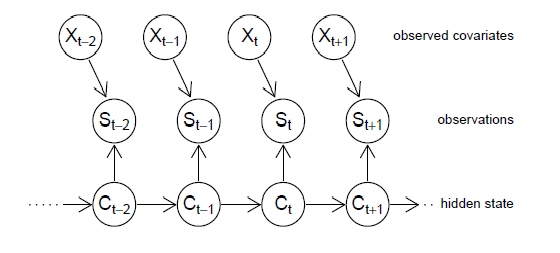
Figura VI.2: HMMs com covariáveis para as probabilidades de estado dependentes.
Tomamos \(\{C_t\}\) como a habitual Cadeia de Markov, e supomos, no caso dos HMMs Poisson, que a média condicional \(\lambda_{ti}\), onde o índice \(t\) indica que a média muda no tempo, depende do vetor linha \(x_t\) das \(q\) covariáveis, por exemplo, como a seguir: \begin{equation} \log\big( \lambda_{ti}\big) \, = \, \beta_i x_t^\top\cdot \end{equation}
No caso de HMMs Binomiais, a suposição correspondente é que \begin{equation} \mbox{logit}\big( \pi_{ti}\big) \, = \, \beta_i x_t^\top\cdot \end{equation}
Os elementos do \(x_t\) poderiam incluir uma constante, tempo \(t\), componentes sinusoidais expressando sazonalidade, por exemplo, \(\cos(2\pi \, t/r)\) e \(\sin(2\pi\, t/r)\) para alguns \(r\) inteiros positivos e quaisquer outras covariáveis relevantes. Por exemplo, um HMM Binomial com \begin{equation} \mbox{logit}\big( \pi_{ti}\big) \, = \, \beta_{i1}+\beta_{i2}t + \beta_{t3}\cos(2\pi \, t/r)+\beta_{i4} \sin(2\pi \, t/4)+\beta_{i5} y_t+\beta_{i6}z_t, \end{equation} permite uma tendência temporal logística linear, sazonalidade do período \(r\) e a influência das covariáveis \(y_t\) e \(z_t\), nas probabilidades de sucesso dependentes do estado \(\pi_{ti}\). Pares seno-cosseno adicionais podem ser incluídos, se necessário, para modelar padrões sazonais mais complexos. Modelos semelhantes para o logaritmo da média condicional \(\lambda_{ti}\) são possíveis no caso do HMM Poisson. Claramente funções de ligação para além das canônicas aqui utilizadas também podem ser consideradas. A expressão para a verossimilhança de \(T\) observações consecutivas \(s_1,\cdots,s_T\) para estes modelos envolvendo covariáveis, ou seja \begin{equation} L_T \, = \, \delta P_1(s_1)\, \Gamma P_2(s_2)\cdots \Gamma P_T(s_t)\pmb{1}^\top, \end{equation} é semelhante ao do caso básico. A única diferença é a dependência das probabilidades dependentes do estado em relação às covariáveis, ou seja, a definição precisa de \(p_{_{ti}}(s_t)\), e portanto de \begin{equation} P_t(s_t) \, = \, \mbox{diag}\big( p_{_{t1}}(s_t),\cdots,p_{_{tm}}(s_t)\big)\cdot \end{equation}
Vale notar que os HMMs Binomial e Poisson, que permitem covariáveis desta forma, fornecem generalizações úteis da regressão logística e da regressão Poisson respectivamente: uma generalização que abandona a hipótese de independência de tais modelos de regressão e permite a dependência em série.
Uma forma alternativa de modelar a tendência temporal e a sazonalidade nos HMMs é abandonar a hipótese de que a Cadeia de Markov seja homogênea e assumir, em vez disso, que as probabilidades de transição são uma função do tempo, ou seja, \begin{equation} \Gamma_t \, = \, \begin{pmatrix} \gamma_{11,t} & \gamma_{12,t} \\ \gamma_{21,t} & \gamma_{22,t} \end{pmatrix}\cdot \end{equation}
De modo mais geral, as probabilidades de transição podem ser modeladas como dependendo de um ou mais covariáveis, não necessariamente o tempo, mas quaisquer variáveis que sejam consideradas relevantes.
A incorporação de covariáveis na Cadeia de Markov não é tão simples como a incorporação das mesmas nas probabilidades dependentes do estado. Uma das razões pelas quais poderia valer a pena, no entanto, é que a Cadeia de Markov resultante possa ter uma interpretação substantiva útil, por exemplo, como um processo meteorológico que é em si mesmo complexo, mas que determina as probabilidades de chuva em vários locais de forma bastante simples.
Vamos ilustrar uma maneira pela qual é possível modificar as probabilidades de transição da Cadeia Markov para modelar a tendência temporal e a sazonalidade. Considere um modeo baseado numa Cadeia de Markov com dois estados \(\{C_t\}\) e \begin{equation} P(C_t=2 \, | \, C_{t-1}=1 ) \, = \, \gamma_{1,t}, \qquad P(C_t=1 \, | \, C_{t-1}=2 ) \, = \, \gamma_{2,t}, \end{equation} para \(i=1,2\) \begin{equation} \mbox{logit}\big( \gamma_{i,t}\big) \, = \, \beta_i x_t^\top\cdot \end{equation}
Por exemplo, um modelo que incorpora a sazonalidade de período \(r\) é \begin{equation} \mbox{logit}\big( \gamma_{i,t}\big) \, = \, \beta_{i1}+\beta_{i2} \cos(2\pi \, t/r)+\beta_{i3}\sin(2\pi \, t/r)\cdot \end{equation} Em geral, a suposição acima em \(\mbox{logit}\big( \gamma_{i,t}\big)\) implica que a matriz de probabilidades de transição, para transições entre os tempos \(t-1\) e \(t\), é dada por \begin{equation} \Gamma_t \, = \, \begin{pmatrix} \displaystyle \dfrac{1}{1+\exp(\beta_1 x_t^\top)} & \displaystyle \dfrac{\exp(\beta_1 x_t^\top)}{1+ \exp(\beta_1 x_t^\top)} \\ \displaystyle \dfrac{\exp(\beta_2 x_t^\top)}{1+\exp(\beta_2 x_t^\top)} & \dfrac{1}{1+\exp(\beta_2 x_t^\top)} \end{pmatrix}\cdot \end{equation}
A extensão deste modelo para o caso \(m > 2\) apresenta dificuldades, mas não parecem ser insuperáveis.
Uma diferença importante entre a classe de modelos aqui propostos e outros HMMs e uma consequência da não homogeneidade, é que nem sempre podemos assumir que haja uma distribuição estacionária para a Cadeia de Markov. Este problema surge quando um ou mais das covariáveis são funções do tempo, como nos modelos de tendência ou sazonalidade. Portanto, se necessário, assumimos, em vez disso, alguma distribuição inicial \(\delta\), no tempo \(t = 1\).
Uma classe muito geral de modelos em que a Cadeia de Markov é não homogênea e que permite a influência dos covariáveis é a de Hughes (1993). Este modelo, e adicionais detalhes relativos aos modelos acima descritos, são apresentados no Capítulo 3 em MacDonald and Zucchini (1997).
Na Seção VI.2 descrevemos uma classe de modelos que têm dependências além daquelas encontradas no HMM básico: HMMs de segunda ordem. Nesse caso, as dependências adicionais estão inteiramente ao nível do processo latente. Aqui descrevemos brevemente três outras classes de modelos com dependências adicionais.
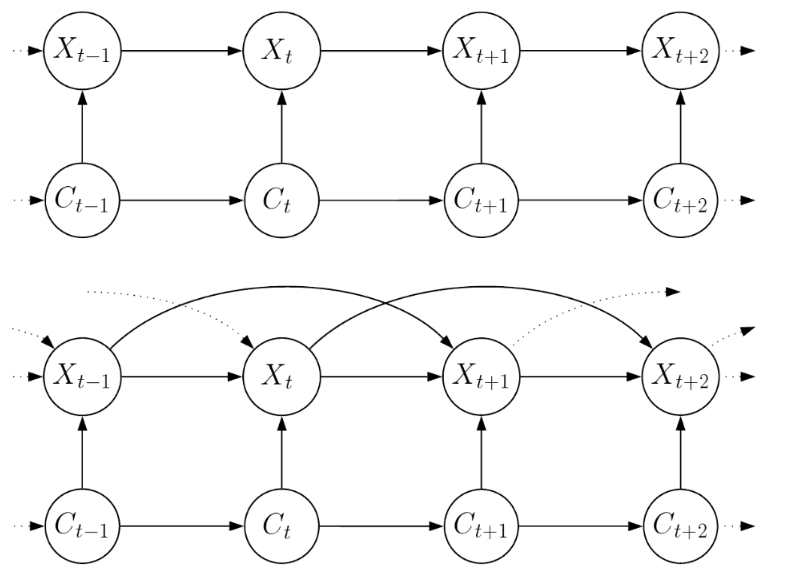
Figura VI.3: Modelos com dependências adicionais no nível de observação, o gráfico superior representa um modelo de Markov AR(1) e o inferior um Markov AR(2).
No modelo básico não há bordas conectando diretamente as observações anteriores ao \(S_t\), a única dependência entre as observações surge do processo latente \(\{C_t\}\). No entanto, pode haver aplicações em que se suspeite de dependências extras ao nível da observação e que devem ser permitidas no modelo.
As características computacionais adicionais de tais modelos são que as probabilidades dependentes do estado necessárias para o cálculo da verossimilhança dependem de observações anteriores, bem como do estado atual e que a verossimilhança maximizada é convenientemente considerada como aquela que é condicional às primeiras observações. A Figura VI.3 mostra dois modelos com tais dependências extras no nível de observação.
Alguns modelos com dependências adicionais a nível de observação que apareceram na literatura são o modelo de Cadeia Markov dupla de Berchtold (1999), os modelos M1-Mk proposto por Nicolas et. al. (2002) para sequência de DNA, os de Boys and Henderson (2004) e os modelos de Markov \(AR(k)\) ocultos, geralmente chamados de autoregressões de Markov.
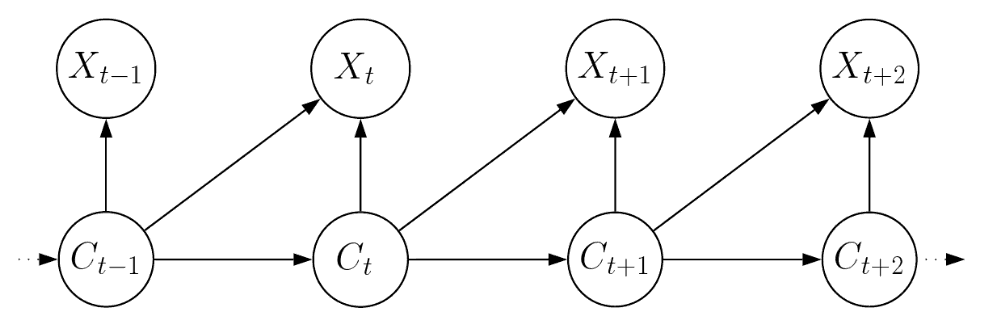
Figura VI.4: Dependências adicionais desde o processo latente até ao nível de observação.
Há outro tipo de dependência extra que pode ser útil. No modelo básico, a distribuição de uma observação depende apenas do estado atual. Não é difícil, no entanto, fazer a menor generalização necessária para que essa distribuição dependa também do estado anterior. A Figura VI.4 mostra o modelo resultante. Se definirmos a matriz \(m\times m\) \(Q(x)\), para ter como seu \((i,j)\) elemento o produto \begin{equation} \gamma_{ij}P\big( S_t=s_t \, | \, C_{t-1}=i, C_t=j\big) \end{equation} e denotando por \(\delta\) a distribuição de \(C_1\), a verossimilhança é dada por \begin{equation} L_T \, = \, \delta P(s_1) Q(s_2)Q(s_3) \cdots Q(s_T)\pmb{1}^\top\cdot \end{equation} Se, em vez disso, denotarmos por \(\delta\) a distribuição de \(C_0\) e não de \(C_1\), o resultado é um pouco mais limpo: \begin{equation} L_T \, = \, \delta Q(s_1) Q(s_2)Q(s_3) \cdots Q(s_T)\pmb{1}^\top\cdot \end{equation}