III. Procedimentos em \(k\) amostras

No problema geral de uma amostra, os dados disponíveis consistem em um único conjunto de observações, geralmente uma amostra aleatória, de uma função de distribuição \(F_X\) da qual as inferências podem ser baseadas em algum aspecto. Os testes de aleatoriedade referem-se a inferências sobre uma propriedade da distribuição de probabilidade conjunta de um conjunto de observações que são distribuídas identicamente mas possivelmente dependentes, ou seja, a distribuição de probabilidade dos dados. A hipótese em um estudo de adequação do ajuste diz respeito à distribuição populacional univariada a partir da qual um conjunto de variáveis independentes é desenhado. Essas hipóteses são tão gerais que não existem contrapartes análogas no domínio da estatística paramétrica. Assim, esses problemas são mais adequados para serem vistos em procedimentos não paramétricos. Em um problema clássico de inferência de uma amostra, os dados de amostra única são usados para obter informações sobre algum aspecto particular da distribuição da população, geralmente um ou mais dos seus parâmetros. Técnicas não paramétricas são úteis aqui também, particularmente quando um parâmetro de locação é de interesse.

III.1 Procedimentos de amostra única e com amostras pareadas

Agora nos preocuparemos com procedimntos não-paramétricos análogos ao teste de média na teoria normal com variância conhecida ou com o teste \(t-Student\) quando a variância é desconhecida para as hipóteses \(H_0 \,: \mu = \mu_0\) e \(H_0 \,: \mu_X -\mu_Y \, = \, \mu_D \, = \, \mu_0\) para os problemas de amostra única e amostras pareadas, respectivamente. Os testes clássicos são derivados sob a suposição que a população única ou a população de diferenças de pares é normal. Para os testes não paramétricos, no entanto, apenas hipóteses de continuidade sobre as populações precisam ser postuladas para determinarmos as distribuições amostrais das estatísticas de teste. As hipóteses aqui estão preocupadas com a mediana ou algum outro quantil em vez da média como o parâmetro de locação, mas tanto a média quanto a mediana são bons índices de tendência central e eles coincidem para populações simétricas. Em qualquer população, a mediana sempre existe o que não é verdade para a média e é mais robusta como uma estimativa de locação. Os procedimentos cobertos aqui incluem intervalos de confiança e testes de hipóteses sobre qualquer quantil. O caso da mediana é tratado separadamente e o teste de sinais assim como o teste dos postos sinalizados de Wilcoxon são apresentados. A discussãão completa em cada caso será dada apenas para a amostra caso, uma vez que com dados de amostras pareadas, uma vez que as observações são formadas, temos essencialmente apenas uma única amostra extraída da população de diferenças e, portanto, os métodos de análise são idênticos.

III.1.1 Intervalo de confiança para o quantil populacional

Lembremos que um quantil de uma variável aleatória contínua \(X\) é um número real que divide a área sob a função de densidade em duas partes de quantidades especificadas. Somente a área à esquerda do número precisa ser especificada, já que a área inteira é igual a 1. Seja \(F_X\) a funço de distribuição subjacente e seja \(\kappa_p\), para todo \(0 < p < 1\), \(p\)-ésimo quantile ou o quantil de ordem \(p\) de \(F_X\). Assim, \(\kappa_p\) é definido como qualquer número real que seja uma solução para a equação \begin{equation} F_X(\kappa_p) \, = \, p, \end{equation} e em termos da função quantil \(\kappa_p \, = \, Q_X(p) \, = \, F_X^{-1}(p)\).

Vamos supor aqui que existe uma solução única, como seria o caso de uma função estritamente crescente \(F_X\). Note que \(\kappa_p\) é um parâmetro da população \(F_X\) e para enfatizar este ponto usamos a letra grega \(\kappa_p\). Por exemplo, \(\kappa_{0.50}\) é a mediana da distribuição, uma medida de tendência central.

Primeiro, consideramos o problema em que uma estimativa do intervalo de confiança do parâmetro \(\kappa_p\) é desejada para algum valor especificado de \(p\), dada uma amostra aleatória \(X_1,X_2,\cdots,X_n\) da função de distribuição \(F_X\). Como discutido, uma estimativa pontual natural de \(\kappa_p\) seria o \(p\)-ésimo quantil amostral, que é a estatística de ordem \(np\), desde claro, que \(np\) seja um inteiro. Por exemplo, como o \(100 p\) por cento dos valores da população são menores ou iguais ao \(p\)-ésimo quantil da população a estimativa de \(\kappa_p\) é o valor de uma amostra aleatória de modo que \(100 p\) por cento dos valores da amostra sejam menores ou iguais a ela. Definamos \(X_{(r)}\) como sendo o \(p\)-ésimo quantil amostral onde \(r\) é definido como \begin{equation} r \, = \, \left\{ \begin{array}{cl} np & \mbox{se } np \mbox{ é um inteiro} \\ [np+1] & \mbox{se } np \mbox{ não é um inteiro}\end{array}\right. \end{equation} e \([x]\) denota o maior número inteiro que não excede \(x\). Esta é apenas uma convenção adotada para que possamos lidar com situações em que \(np\) não é um inteiro. Outras convenções são por vezes adotadas. No nosso caso, o \(p\)-ésimo quantil amostral \(Q_X(p)\) é igual a \(X_{(np)}\) se \(np\) for um inteiro, e \(X_{([np+1])}\) se \(np\) não for um inteiro.

Uma estimativa pontual não é suficiente para fins de inferência. Sabemos que a estatística de ordem \(r\) é um estimador consistente do \(p\)-ésimo quantil de uma distribuição quando \(n\to\infty\) e \(r/n\to p\). No entanto, a consistência é apenas uma propriedade em amostras grandes. Gostaríamos de um procedimento para a estimativa do intervalo de \(\kappa_p\) que nos permita anexar um coeficiente de confiança à nossa estimativa para um tamanho de amostra dado finito. Uma escolha lógica para os pontos extremos do intervalo de confiança são duas estatísticas de ordem, digamos \(X_{(r)}\) e \(X_{(s)}\), sendo \(r < s\), obtidas da amostra aleatória extraída da população \(F_X\). Para encontrar o \(100(1-\alpha)\)% intervalo de confiança, devemos então encontrar os dois inteiros \(r\) e \(s\), \(1\leq r < s\leq n\) tais que \begin{equation} P(X_{(r)} \, < \, \kappa_p \, < \, X_{(s)}) \, = \, 1-\alpha, \end{equation} para algum dado número \(0 < \alpha < 1\).

A quantidade \(1-\alpha\), que frequentemente denotamos por \(\gamma\), é chamado de nível de confiança ou coeficiente de confiança. Agora o evento \(X_{(r)} < \kappa_p\) ocorre se, e somente se, \(X_{(r)} < \kappa_p < X_{(s)}\) ou \(\kappa_p> X_{(s)}\), e esses dois últimos eventos são claramente mutuamente exclusivos. Portanto, para todos os \(r < s\), \begin{equation} P(X_{(r)} \, < \kappa_p) \, = \, P(X_{(r)} \, < \kappa_p < X_{(s)}) + P(\kappa_p>X_{(s)}) \end{equation} ou equivalentemente \begin{equation} P(X_{(r)} \, < \kappa_p \, < X_{(s)}) \, = \, P(X_{(r)}<\kappa_p) \, - \, P(X_{(s)}<\kappa_p)\cdot \end{equation}

Desde que assumimos que \(F_X\) é uma função estritamente crescente \begin{equation} X_{(r)} \, < \, \kappa_p \qquad \mbox{se, e somente se,} \qquad F_X(X_{(r)}) \, < \, F_X(\kappa_p) \, = \, p\cdot \end{equation} Mas quando o \(F_X\) é contínua, a distribuição de probabilidade da variável aleatória \(F(X_{(r)})\) é a mesma que a de \(U_{(r)}\), a \(r\)-ésima estatística de ordem a partir da distribuição uniforme ao longo do intervalo \((0,1)\). Além disso, como \(F_X(\kappa_p)=p\) pela definição de \(\kappa_p\), temos \begin{equation} P(X_{(r)}<\kappa_p) \, = \, P\big( F_X(X_{(r)})< p\big) \, = \, \int_0^p \dfrac{n!}{(r-1)!(n-r)!}x^{r-1}(1-x)^{n-r}\mbox{d}x\cdot \end{equation} Assim, enquanto a distribuição da \(r\)-ésima estatística de ordem depende da distribuição da população \(F_X\), a probabilidade acima não. Podemos então obter um intervalo de confiança livre de distribuição.

A fim de encontrar a estimativa do intervalo de \(\kappa_p\), observamos que \(r\) e \(s\) devem ser escolhidos de tal forma que \begin{equation} \int_0^p n{n-1 \choose r-1}x^{r-1}(1-x)^{n-r}\mbox{d}x \, - \, \displaystyle \int_0^p n{n-1 \choose s-1}x^{s-1}(1-x)^{n-s}\mbox{d}x \, = \, 1-\alpha\cdot \end{equation} Claramente, esta equação não dará uma solução única para os dois desconhecidos \(r\) e \(s\) e condições adicionais são necessárias. Por exemplo, se quisermos o intervalo mais estreito possível para um coeficiente de confiança fixo, \(r\) e \(s\) devem ser escolhidos de tal forma que a realação acime seja satisfeita e \(X_{(s)}-X_{(r)}\) ou \(\mbox{E}\big| X_{(s)}-X_{(r)} \big|\) seja o menor possível. Alternativamente, poderíamos minimizar \(s- r\).

Contudo, \(P(X_{(r)}<\kappa_p)\) pode ser expresso de outra forma após a integração por partes segue: \begin{equation} \begin{array}{rcl} P(X_{(r)}<\kappa_p) & = & \displaystyle \int_0^p n{n-1 \choose r-1}x^{r-1}(1-x)^{n-r}\mbox{d}x \\ & = & \displaystyle n{n-1 \choose r-1}\Big[ \left.\frac{x^r}{r}(1-x)^{n-r}\right|_0^p+\dfrac{n-r}{r}\int_0^p x^{r}(1-x)^{n-r-1}\mbox{d}x \Big] \\ & = & \displaystyle {n \choose r}p^r(1-p)^{n-r} + n{n-1 \choose r}\Big[ \left.\frac{x^{r+1}}{r+1}(1-x)^{n-r-1}\right|_0^p+\dfrac{n-r-1}{r+1}\int_0^p x^{r+1}(1-x)^{n-r-2}\mbox{d}x \Big] \\ & = & \displaystyle {n \choose r}p^r(1-p)^{n-r} + {n \choose r+1}p^{r+1}(1-p)^{n-r-1} \, + \, \displaystyle n{n-1 \choose r+1}\int_0^p x^{r+1}(1-x)^{n-r-2}\mbox{d}x \cdot \end{array} \end{equation}

Depois de repetir essa integração por partes \(n-r\) vezes, o resultado será \begin{equation} \begin{array}{r} \displaystyle {n \choose r}p^r(1-p)^{n-r} \, + \, \displaystyle {n \choose r+1}p^{r+1}(1-p)^{n-r-1} \, + \, \cdots \, + \, \displaystyle {n \choose n-1}p^{n-1}(1-p) \, + \, \displaystyle n{n-1 \choose n-1}\int_0^p x^{n-1}(1-x)^{0}\mbox{d}x \, = \, \\ = \, \displaystyle \sum_{j=0}^{n-r}{n \choose r+j}p^{r+j}(1-p)^{n-r-j}, \end{array} \end{equation} ou, depois de substituir \(r+j=i\), \begin{equation} P(X_{(r)}<\kappa_p) \, = \, \displaystyle \sum_{i=r}^n {n \choose i}p^i(1-p)^{n-i}\cdot \end{equation}

Nesta forma final, a integral em é expressa como a soma dos últimos \(n-r+1\) termos da distribuição binomial com os parâmetros \(n\) e \(p\). Assim, a probabilidade \(P(X_{(r)} \, < \kappa_p \, < X_{(s)})\) pode ser expressa como \begin{equation} \begin{array}{rcl} P(X_{(r)} \, < \kappa_p \, < X_{(s)}) & = & \displaystyle \sum_{i=r}^n {n \choose i}p^i(1-p)^{n-i} \, - \, \sum_{i=s}^n p^i(1-p)^{n-i} \\ & = & \displaystyle \sum_{i=r}^{s-i} {n \choose i}p^i(1-p)^{n-i} \, = \, P(r \, \leq K \leq s-1), \end{array} \end{equation} onde \(K\) tem distribuição binomial com os parâmetros \(n\) e \(p\). Esta forma é provavelmente o mais fáácil de usar na escolha de \(r\) e \(s\) tal que \(s- r\) é mínimo para \(\alpha\) fixo. Note que a partir da expressão acima está claro que esta probabilidade não depende da função de distribuição subjacente, desde que seja contínua. O intervalo de confiança resultante é, portanto, livre de distribuição.

Para encontrar o intervalo de confiança para \(\kappa_p\) com base em estatísticas bilaterais, o lado direito de acima é igual a \(1-\alpha\) e a busca por \(r\) e \(s\) é iniciada. Por causa da distribuição binomial ser discreta, o nível de confiança nominal exato frequentemente não pode ser alcançado. Nesses casos, o nível de confiança requerido pode ser alterado de "igual a" para "pelo menos igual a" \(1-\alpha\). Geralmente denotamos \(\gamma\geq 1-\alpha\) como o nível de confiança exato.

Note que para qualquer \(p\), o evento \(X_{(r)} < \kappa_p\) ocorre se, e somente se, pelo menos \(r\) dos \(n\) valores da amostra, \(X_1,X_2,\cdots,X_n\), são menores que \(\kappa_p\). Portanto \begin{equation} \begin{array}{rcl} P(X_{(r)} \, < \kappa_p ) & = & \displaystyle P(\mbox{exatamente } r \mbox{ das } n \mbox{ observações são } > \kappa_p) + \\ & & + P(\mbox{exatamente } r+1 \mbox{ das } n \mbox{ observações são } < \kappa_p) + \\ & & \cdots + P(\mbox{exatamente } n \mbox{ das } n \mbox{ observações são } < \kappa_p), \end{array} \end{equation} Em outras palavras \begin{equation} P(X_{(r)} \, < \kappa_p ) \, = \, \displaystyle \sum_{i=r}^n P(\mbox{exatamente } i \mbox{ das } n \mbox{ observações são } < \kappa_p)\cdot \end{equation}

Esta é uma observação chave. Agora, a probabilidade de que exatamente \(i\) das \(n\) observações sejam menores que \(\kappa_p\) pode ser encontrada como a probabilidade de \(i\) sucessos em \(n\) tentativas independentes de Bernoulli, já que as observa\ções da amostra são todas independentes e cada observação pode ser classificada como um sucesso ou uma falha, onde um sucesso é definido como qualquer observação sendo menor que \(\kappa_p\). A probabilidade de sucesso é \(P(X_i < \kappa_p)=p\). Assim, a probabilidade requerida é dada pela probabilidade binomial com os parâmetros \(n\) e \(p\). Em outras palavras, \begin{equation} P(\mbox{exatamente } i \mbox{ das } n \mbox{ observações são } < \kappa_p) \, = \, \displaystyle {n \choose i}p^i (1-p)^{n-i}, \end{equation} e, portanto, \begin{equation} P(X_{(r)} \, < \kappa_p ) \, = \, \displaystyle \sum_{i=r}^n{n \choose i}p^i(1-p)^{n-i}\cdot \end{equation}

Em resumo, o intervalo de confiança com nível de confiança \((1-\alpha)100\)% para o \(p\)-ésimo quantil é dado por \(\big( X_{(r)}, \, X_{(s)}\big)\), onse \(r\) e \(s\) são inteiros tais que \(1\leq r< s\leq n\) e \begin{equation} P(X_{(r)} \, < \kappa_p \, < X_{(s)}) \, = \, \displaystyle \sum_{i=r}^{s-1}{n \choose i}p^i (1-p)^{n-i} \, \geq \, 1-\alpha\cdot \end{equation}

Como indicado anteriormente, sem uma segunda condição, os pontos finais do intervalo de confiança não serão exclusivos. Uma abordagem comum neste caso é atribuir a probabilidade \(\alpha/2\) em cada cauda, direita e esquerda. Isso produz o chamado intervalo de "igualdade de caudas", onde \(r\) e \(s\) são os maiores e menores inteiros \(1\leq r< s\leq n\) respectivamente, de tal forma que \begin{equation} \sum_{i=0}^{r-1}{n \choose i}p^i(1-p)^{n-i}\leq \frac{\alpha}{2} \qquad \mbox{e} \qquad \displaystyle \sum_{i=0}^{s-1}{n \choose i}p^i(1-p)^{n-i}\geq 1-\frac{\alpha}{2} \end{equation} respectivamente. Essas equações são fáceis de usar desde que sejam fornecidas probabilidades binomiais acumuladas. O nível de confiança exato é encontrado como \begin{equation} \sum_{i=r}^{s-1}{n \choose i}p^i (1-p)^{n-i} \, = \, \displaystyle \sum_{i=0}^{s-1}{n \choose i}p^i(1-p)^{n-i} \, - \, \sum_{i=0}^{r-1}{n \choose i}p^i(1-p)^{n-i} \, = \, \gamma\cdot \end{equation}

Se o tamanho da amostra for maior que 20 e, portanto, podemos usar a aproximação normal para a distribuição binomial com uma correção de continuidade. As soluções são \begin{equation} r \, = \, np + 0.5 - z_{\alpha/2}\sqrt{np(1-p)} \qquad \mbox{e} \qquad s \, = \, np+0.5+z_{\alpha/2}\sqrt{np(1-p)} \end{equation} onde \(z_{\alpha/2}\) satisfaz \(\Phi(z_{\alpha/2})=1-\alpha/2\). Arredondamos o resultado de \(r\) acima para o inteiro mais próximo e arredondamos o resultado de \(s\) acima para cima, para ser conservador ou para tornar o nível de confiança ao menos \(1-\alpha\).

III.1.2 Teste de hipótese para um quantil populacional

Dada a estatística de ordem \(X_{(1)}\leq X_{(2)}\leq \cdots \leq X_{(n)}\) de qualquer função de distribuição absolutamente continua \(F_X\) não especificada, uma hipótese nula relativa ao valor do \(p\)-ésimo quantil é escrita como \begin{equation} \kappa_p = \kappa_p^0, \end{equation} onde \(\kappa_p^0\) e \(p\) são ambos especificados. Sob \(H_0\), como \(\kappa_p^0\) é o \(p\)-ésimo quantil de \(F_X\), temos, por definição \(P(X\leq \kappa_p^0)=p\) e, portanto, esperamos que cerca de \(np\) das observações amostrais sejam menores que \(\kappa_p^0\) se \(H_0\) for verdadeira. Se o número real de observações amostrais menores que \(\kappa_p^0\) for consideravelmente menor que \(np\), os dados sugerem que o verdadeiro \(p\)-ésimo quantil é maior que \(\kappa_p^0\) ou há evidência contra \(H_0\) em favor da alternativa unilateral de cauda superior \begin{equation} H_1: \kappa_p\geq \kappa_p^0\cdot \end{equation}

Isto implica que é razoável rejeitar \(H_0\) em favor de \(H_1\) se, no máximo, \(r-1\) observações amostrais são menores que \(\kappa_p^0\), para alguns \(r\). Agora, se no máximo \(r-1\) observações amostrais são menores que \(\kappa_p^0\), então deve ser verdade que a estatística de ordem \(X_{(r)}\) na amostra satisfaz \(X_{(r)}> \kappa_p^0\). Portanto, uma região de rejeição apropriada \(\Omega_1\) é \begin{equation} X_{(r)}\in \Omega_1, \qquad \mbox{para} \qquad X_{(r)}>\kappa_p^0\cdot \end{equation}

Para um nível de significância especificado \(\alpha\), o inteiro \(r\) deve ser escolhido de forma que \begin{equation} P(X_{(r)}> \kappa_p^0 \, | \, H_0) \, = \, 1-P(X_{(r)}\leq \kappa_p^0 \, | \, H_0) \, \leq \, \alpha \end{equation} ou \(r\) é o maior inteiro tal que \begin{equation} 1-\sum_{i=r}^n {n \choose i}p^i (1-p)^{n-i} \, = \, \sum_{i=0}^{r-1}{n \choose i}p^i(1-p)^{n-i} \, \leq \, \alpha\cdot \end{equation}

Agora expressamos a região de rejeição em outra forma para ser consistente com nossa apresentação posterior para o teste de sinais. Note que \(X_{(r)}> \kappa_p^0\) se, e somente se, no máximo \(r-1\) das observações são menores que \(\kappa_p^0\), de modo que pelo menos \(n-(r-1)=n-r+1\) das observações são maiores que \(\kappa_p^0\).

Definamos a variável aleatória \(K\) como o número total de sinais positivos entre as diferenças \(X_{(i)} - \kappa_p^0\) ou seja, o número de diferenças positivas. Então a região de rejeição pode ser equivalente declarada como \begin{equation} K\in\Omega_1 \qquad \mbox{para} \qquad K\geq n-r+1\cdot \end{equation}

As diferenças \(X_i - \kappa_p^0\), \(i=1,2,\cdots,n\), são variáveis aleatórias independentes, cada uma tendo um sinal de mais ou menos e a probabilidade de um sinal de mais sob \(H_0\) é \begin{equation} P(X_i - \kappa_p^0>0) \, = \, P(X_i > \kappa_p^0) \, = \, 1-p\cdot \end{equation} Portanto, como \(K\) é o número de sinais positivos, podemos escrever \begin{equation} K \, = \, \sum_{i=1}^n \pmb{1}(X_i > \kappa_p^0), \end{equation} onde \(\pmb{1}(X_i > \kappa_p^0)=1\) quando o evento \(A\) ocorre e é 0 caso contrário. Da discussão anterior, as variáveis indicadoras \(\pmb{1}(X_i > \kappa_p^0)\), \(i=1,2,\cdots,n\) são variáveis aleatórias independentes com função de probabilidade \(Bernoulli(1-p)\) sob \(H_0\). Assim, sob \(H_0\), a distribuição de \(K\) é \(Binomial(n, 1-p)\) e so \(r\) devem ser escolhidos para satisfazer \begin{equation} P(K\geq n-r+1 \, | \, H_0) \, = \, \sum_{i=n-r+1}^n {n \choose i}(1-p)^i p^{n-i} \, \leq \, \alpha\cdot \end{equation}

Por outro lado, se muito mais do que \(np\) observações são menores que \(\kappa_p^0\), há suporte contra \(H_0\) em favor da alternativa unilateral de cauda inferior \(H_1: \kappa < \kappa_p^0\). Então devemos rejeitar \(H_0\) se o número de observações amostrais menores que \(\kappa_p^0\) for pelo menos, digamos \(s\). Isso leva à região de rejeição \begin{equation} X_{(s)}\in \Omega_1 \qquad \mbox{para} \qquad X_{(s)}<\kappa_p^0, \end{equation} mas isso equivale a dizer que o número de observações maiores que \(\kappa_p^0\) deve ser no máximo \(n-s\). Assim, com base na estatística \(K\), definida antes como o número de diferenças positivas, a região de rejeição apropriada para a alternativa unilateral de cauda inferior \(H_1 \,: \kappa_p < \kappa_p^0\) é \begin{equation} K\in\Omega_1 \qquad \mbox{para} \qquad K\leq n-s, \end{equation} onde \(s\) é o maior número inteiro tal que \begin{equation} P(K\leq n-s \, | \, H_0) \, = \, \sum_{i=0}^{n-s} {n \choose i}(1-p)^i p^{n-i} \, \leq \, \alpha\cdot \end{equation}

Para a alternativa bilateral \(H_1 \,: \kappa_p\neq \kappa_p^0\), a região de rejeição consiste na união das duas partes especificadas acima, \begin{equation} K\in\Omega_1 \qquad \mbox{para} \qquad K\leq n-s \qquad \mbox{ou} \qquad K\geq n-r+1, \end{equation} onde \(r\) e \(s\) são inteiros tais que a probabilidade associada é menor ou igual a \(\alpha/2\).

III.1.3 Procedimento com amostras pareadas

Os procedimentos de teste de sinais de uma amostra para teste de hipóteses e estimação por intervalo de confiança de \(M\) são igualmente aplicáveis a dados de amostras pareadas. Para uma amostra aleatória de \(n\) pares \((X_1,Y_1),\cdots,(X_n,Y_n)\), construímos as \(n\) diferenças \(D_i=X_i-Y_i\). Se a população das diferenças é assumida contínua na sua mediana \(M_D\), de modo que \(P(D=M_D)=0\) e \(\theta\) é definida como \(\theta=P(D>M_D)\), os mesmos procedimentos são claramente válidos aqui com \(X_i\) substituído em todo lugar por \(D_i\).

Deve ser enfatizado que este é um teste para a diferença mediana \(M_D\), que não é necessariamente a mesma que a diferença das duas medianas \(M_X\) e \(M_Y\). O exemplo simples a seguir servirá para ilustrar esse fato muitas vezes mal compreendido. Seja a função de densidade conjunta de \(X\) e \(Y\) \begin{equation} f_{X,Y}(x,y)=\left\{ \begin{array}{rcl} 1/2, & caso & y-1\leq x\leq y, \quad -1\leq y\leq 1 \\ & ou & y+1\leq x\leq 1, \quad -1\leq y\leq 0 \\ 0, & caso & contrário \end{array} \right. \cdot \end{equation}

Então \(X\) e \(Y\) são uniformemente distribuídos sobre a região sombreada na figura abaixo. Pode ser visto que as distribuições marginais de \(X\) e \(Y\) são idênticas, ambas sendo uniformes no intervalo \((-1,1)\), de modo que \(M_X = M_Y = 0\). É claro que onde \(X\) e \(Y\) têm sinais opostos, nos quadrantes II e IV, \begin{equation} P(X < Y) = P(X > Y), \end{equation} enquanto nos quadrantes I e III, \(X < Y\) sempre. Para todos os pares, então, temos \(P( X < Y) = 3/4\), o que implica que a mediana da população das diferenças é menor que zero. A função de distribuição da variável aleatória diferença \(D=X-Y\) é \begin{equation} F_D(d)=\left\{ \begin{array}{ccc} 0, & caso & d\leq -1 \\ \displaystyle \frac{(d+1)(d+3)}{4}, & caso & -1< d\leq 0 \\ \displaystyle \frac{3}{4} & caso & 0< d\leq 1 \\ \displaystyle \frac{d(4-d)}{4}, & caso & 1< d \leq 2 \\ 1, & caso & d\ge 2 \end{array} \right. \cdot \end{equation}

A diferença mediana é o valor \(M_D\), da distribuição de \(D\), tal que \(F_D(M_D)=1/2\). Pode-se verificar que isso produz \(M_D=-2+\sqrt{3}\).

Em geral, então, não é verdade que \(M_D=M_X-M_Y\). Por outro lado, é verdade que a média das diferenças é igual à diferença das médias. Como a média e a mediana coincidem para as distribuições simétricas, se as populações \(X\) e \(Y\) são simétricas e \(M_X=M_Y\) e se a população das diferenças também é simétrica. A população das diferenças é simétrica se \(X\) e \(Y\) forem simétricos e independentes ou se \(f_{X,Y}(x,y)=f_{X,Y}(-x,-y)\). Então \(M_D=M_X-M_Y\) e \(M_X=M_Y\) são uma condição necessária e suficiente para \(M_D=0\). Observe que para o caso em que \(X\) e \(Y\) são cada uma normalmente distribuídas, a diferença de suas medianas ou de suas médias é igual à mediana ou média de sua diferença \(X-Y\), desde que \(X-Y\) também é normalmente distribuída com mediana ou média igual à diferença das respectivas medianas ou médias.

III.2 O problema geral de duas amostras

Para os testes de pares combinados e postos sinalizados os dados consistiam em duas amostras, mas cada elemento em uma amostra estava vinculado a um elemento particular da outra amostra por alguma unidade de associação. Esta situação de amostragem pode ser descrita como um caso de duas amostras dependentes ou, alternativamente, como uma única amostra de pares de uma população bivariada. Quando as inferências a serem tiradas são relacionadas apenas para a população de diferenças das observações emparelhadas, o primeiro passo na análise geralmente é fazer as diferenças das observações emparelhadas; isso deixa apenas um único conjunto de observações. Portanto, esse tipo de dado pode ser legitimamente classificado como um problema de uma amostra. Agora trataremos de dados que consistem em duas amostras aleatórias mutuamente independentes, ou seja, amostras aleatórias obtidas independentemente de cada uma das duas populações. Não apenas os elementos dentro de cada amostra são independentes, mas também todos os elementos da primeira amostra são independentes de cada elemento na segunda amostra.

O universo consiste em duas populações, que chamamos de populaçõs \(X\) e \(Y\), com funções de distribuição denotadas por \(F_X\) e \(F_Y\), respectivamente. Temos uma amostra aleatória de tamanho \(m\) extraída da população \(X\) e outra amostra aleatória de tamanho \(n\) obtida independentemente da população \(Y\), \begin{equation} X_1,X_2,\cdots,X_m \qquad \mbox{e} \qquad Y_1,Y_2,\cdots,Y_n\cdot \end{equation}

Normalmente, a hipótese de interesse no problema de duas amostras é que as duas amostras são extraídas de populações idênticas, ou seja, \begin{equation} H_0 \, : \, F_Y(x) \, = \, F_X(x), \qquad \mbox{para todo } x\cdot \end{equation} Se estivermos dispostos a fazer suposições paramétricas sobre as formas das populações subjacentes e assumirmos que as diferenças entre as duas populações ocorrem apenas com relação a alguns parâmetros, como as médias ou as variâncias, é frequentemente possível derivar o chamado de teste de Neyman-Pearson. Por exemplo, se assumirmos que as populações são normalmente distribuídas, é bem conhecido que o teste \(t-Student\) de duas amostras para igualdade de médias e o teste \(F-Fisher\) para igualdade de variâncias são, respectivamente, os melhores testes. Os desempenhos destes dois testes são também bem conhecidos.

No entanto, esses e outros testes clássicos podem ser sensíveis a violações dos pressupostos fundamentais do modelo inerentes à derivação e à construção desses testes. Quaisquer conclusões obtidas com esses testes são tão válidas quanto as hipóteses subjacentes feitas. Se houver razão para suspeitar de uma violação de qualquer um desses postulados ou se informações suficientes para julgar sua validade não estiverem disponíveis ou se um teste completamente geral de igualdade para distribuições não especificadas for desejado, algum procedimento não paramétrico está recomendado.

Na prática, outras suposições são frequentemente feitas sobre a forma das populações subjacentes. Uma suposição comum é chamada de modelo de locação. Este modelo assume que as populações \(X\) e \(Y\) são as mesmas em todos os outros aspectos, exceto, possivelmente, por uma mudança na quantidade desconhecida de, digamos, \(\theta\), ou que \begin{equation} F_Y(x) \, = \, P(Y\leq x) \, = \, P(X\leq x-\theta) \, = \, F_X(x-\theta), \qquad \forall x, \; \forall \theta\neq 0 \end{equation}

Isso significa que \(X+\theta\) e \(Y\) têm a mesma distribuição ou que \(X\) é distribuído como \(Y-\theta\). A população \(Y\) é então a mesma que a população \(X\) se \(\theta= 0\), é deslocada para a direita se \(\theta > 0\) e é deslocada para a esquerda se \(\theta < 0 \). Sob a hipótese de mudança, as populações têm a mesma forma e a mesma variâ;ncia, e a quantidade do deslocamento \(\theta\) deve ser igual à diferença entre as médias populacionais, \(\mu_Y- \mu_X\), as medianas populacionais, \(M_Y-M_X\), e de fato a diferença entre quaisquer dois paramâmetros de locação ou quantis da mesma ordem.

Outra suposição sobre a forma da população subjacente é chamado de modelo de escala, este assume que as populações \(X\) e \(Y\) são as mesmas, exceto possivelmente para um fator de escala positivo \(\theta\) que não é igual a um. O modelo de escala pode ser escrito como \begin{equation} F_Y(x) \, = \, P(Y\leq x) \, = \, P(X\leq \theta x) \, = \, F_X(\theta x), \qquad \forall x, \; \forall \theta>0, \, \theta\neq 1\cdot \end{equation} Isto significa que \(X/\theta\) e \(Y\) têm a mesma distribuição para qualquer \(\theta\) positivo ou que \(X\) é distribuído como \(\theta Y\). Além disso, a variância de \(X\) é \(\theta^2\) vezes a variância de \(Y\) e a média de \(X\) é \(\theta\) vezes a média de \(Y\).

Uma suposição mais geral sobre a forma das populações subjacentes é chamado de modelo de locação-escala. Este modelo pode ser escrito como \begin{equation} P(Y-\mu_Y\leq x) \, = \, P(X-\mu_X\leq \theta x), \end{equation} o qual estabelece que \((X-\mu_X)/\theta\) e \(Y-\mu_Y\) são identicamente distribuídas. Assim, o modelo de locação-escala incorpora propriedades dos modelos de locação e de escala. Agora, as médias de \(X- \mu_X\) e \(Y- \mu_Y\) são ambas zero e a variância de \(X- \mu_X\) é \(\theta^2\) vezes a variância de \(Y- \mu_Y\).

Independentemente do modelo assumido, o problema geral de duas amostras talvez seja o problema mais discutido nas estatísticas não-paramétricas. A hipótese nula é quase sempre formulada como populações idênticas, com a distribuição comum completamente não especificada, exceto pela suposição de que é uma função de distribuição contínua. Assim, sob o caso nulo, as duas amostras aleatórias podem ser consideradas uma única amostra aleatória de tamanho \(N = m + n\) extraídas da população comum, contínua, mas não especificada. Então a configuração ordenada combinada das \(m\) variáveis aleatórias \(X\) e as \(n\) \(Y\) na amostra é um dos \({m+n \choose m}\) arranjos possíveis igualmente prováveis.

Por exemplo, suponhamos que temos duas amostras independentes, \(m=3\) de \(X\) e \(n=2\) de \(Y\). Sob a hipótese nula de que \(X\) e \(Y\) são identicamente distribuídas, cada um dos \({5 \choose 2}=10\) possíveis arranjos da amostra combinada mostrados abaixo são igualmente prováveis \begin{equation} \begin{array}{ccccc} 1- XXXYY & 2- XXYXY & 3- YXYXX & 4- XXYYX & 5- XYXXY \\ 6- XYXYX & 7- YXXXY & 8- YXXYX & 9- XYYXX & 10- YYXXX \end{array} \end{equation}

Na prática, o padrão amostral de arranjos de \(X\) e \(Y\) fornece informações sobre o tipo de diferença que pode existir na população. Por exemplo, se o arranjo observado é aquele designado por 1 ou 10 no exemplo acima, \(X\) e o \(Y\) não parecem ser aleatoriamente misturados, sugerindo uma contradição à hipótese nula. Muitos testes estatísticos são baseados em alguma função desse arranjo combinado. O tipo de função mais apropriado depende do tipo de diferença que se espera detectar o que é indicado pela hipótese alternativa. Uma abundância de alternativas razoáveis para \(H_0\) pode ser considerada, mas o tipo mais fácil de analisar usando técnicas distribuição livre declara alguma relação funcional entre as distribuições. As alternativas bilaterais mais gerais são \begin{equation} H_1 \, : \, F_Y(x) \, \neq \, F_X(x), \quad \mbox{para algum } x \end{equation} e a correspondente alternative unilateral geral é \begin{equation} H_1 \, F_Y(x) \, \geq \, F_X(x), \quad \forall x \qquad \mbox{ou} \qquad H_1 \, : \, F_Y(x)> F_X(x), \quad \mbox{para algum } x\cdot \end{equation}

Neste último caso, geralmente dizemos que a variável aleatória \(X\) é estocasticamente maior que a variável aleatória \(Y\). Se a alternativa particular de interesse é simplesmente uma diferença na locação, usamos a alternativa de locação ou o modelo de locação \begin{equation} H_0 \, : \, F_Y(x) \, = \, F_X(x-\theta), \quad \forall x \mbox{ e algum } \theta\neq 0\cdot \end{equation}

Sob o modelo de locação, \(Y\) é distribuído como \(X + \theta\), de modo que \(Y\) é estocasticamente maior ou menor que \(X\) se, e somente, \(\theta> 0\) ou \(\theta < 0\). Da mesma forma, se apenas uma diferença na escala é de interesse, usamos a alternativa de escala \begin{equation} H_1 \, : \, F_Y(x) \, = \, F_X(\theta x), \quad \forall x \mbox{ e algum } \theta\neq 1\cdot \end{equation} Sob o modelo de escala, \(Y\) é distribuído como \(X/\theta\), de modo que \(Y\) é estocasticamente maior ou menor que \(X\) se, e somente se, \(\theta <1\) ou \(\theta> 1\).

III.2.1 Teste de Wald-Wolfowitz

Sejam dois conjuntos de variáveis aleatórias independentes \(X_1,X_2,\cdots,X_m\) e \(Y_1,Y_2,\cdots,Y_n\) combinados em uma única sequência ordenada, do menor para o maior, acompanhando quais observações correspondem à amostra \(X\) e quais à \(Y\). Assumindo que as suas distribuições de probabilidade são contínuas, uma ordenação única é sempre possível, uma vez que teoricamente laços não existem. Por exemplo, com \(m=4\) e \(n=5\), o arranjo pode ser \begin{equation} X Y Y X X Y X Y Y \end{equation} que indica que na amostra agrupada o menor elemento era um \(X\), o segundo menor um \(Y\), etc., e maior um \(Y\). Sob a hipótese nula de distribuições idênticas \begin{equation} H_0 \, : \, F_Y(x) \, = \, F_X(x), \quad \forall x, \end{equation} esperamos que as variáveis aleatórias \(X\) e \(Y\) sejam bem misturadas na configuração ordenada, uma vez que as \(m+n=N\) variáveis aleatórias constituem uma única amostra aleatória de tamanho \(N\) da população comum. Com uma corrida definida como uma sequência de letras idênticas precedido e seguido por uma letra diferente ou nenhuma letra, o número total de execuções na amostra agrupada ordenada é indicativo do grau de mistura. Em nosso arranjo \(X Y Y X X Y X Y Y\), o número total de corridas é igual a 6, o que mostra uma boa mistura de \(X\) e \(Y\).

Um padrão de arranjo com poucas corridas sugeriria que esse grupo de \(N\) não é uma amostra aleatória única, mas sim composto por duas amostras de duas populações distintas. Por exemplo, se a disposição fosse \(X X X X Y Y Y Y Y\), todos os elementos da amostra \(X\) serão menores que todos os elementos da amostra \(Y\), haveria apenas duas corridas. Essa configuração específica pode indicar não apenas que as populações não são idênticas, mas também que os \(X\) são estocasticamente menores que os \(Y\). No entanto, a ordenação reversa também contém apenas duas corridas e, portanto, um critério de teste baseado somente no número total de corridas não pode distinguir esses dois casos.

O teste de corridas é apropriado principalmente quando a alternativa é completamente geral e bilateral, como em \begin{equation} H_1 \, : \, F_Y(x) \, \neq \, F_X(x), \qquad \mbox{para algum } x\cdot \end{equation} Definimos a variável aleatória \(R\) como o número total de corridas no arranjo ordenado combinado de variáveis aleatórias \(m\) \(X\) e \(n\) \(Y\). Uma vez que poucas corridas tendem a desacreditar a hipótese nula quando a alternativa é \(H_1\) acima, o teste de Wald-Wolfowitz (1940) para o nível de significância \(\alpha\) geralmente tem a região de rejeição de cauda inferior como \begin{equation} R\leq c_\alpha, \end{equation} onde \(c_\alpha\) é escolhido como sendo o maior número inteiro satisfazendo \begin{equation} P(R\leq c_\alpha \, | \, H_0) \, \neq \, \alpha\cdot \end{equation} O \(p-valor\) para o teste de corridas é dado por \begin{equation} P(R\leq R_0 \, | \, H_0), \end{equation} onde \(R_0\) é o valor observado da estatística do teste de corridas \(R\).

Como as observações \(X\) e \(Y\) são dois tipos de objetos dispostos em uma sequência completamente aleatória, se \(H_0\) for verdadeira, a distribuição de \(R\) sob a hipóteses nula é exatamente a mesma encontrada para o teste de aleatoriedade. A distribuição foi desenvolvida e aqui substituímos \(n_1\) e \(n_2\) por \(m\) e \(n\), respectivamente, supondo que os \(X\) são chamados de objetos do tipo 1 e os \(Y\) chamados de objetos do tipo 2. Outras propriedades de \(R\) discutidas, incluindo os momentos e a distribuição nula assintótica, também são inalteradas. A única diferença aqui é que a região crítica apropriada para a alternativa de populações diferentes é observarmos pouquíssimas corridas.

O teste de corridas de Wald-Wolfowitz é extremamente geral e consistente contra todos os tipos de diferenças nas populações (Wald e Wolfowitz, 1940). A própria generalidade do teste sinaliza seu desempenho em relação a alternativas específicas. O poder assintótico pode ser avaliado usando a distribuição normal com momentos apropriados sob a alternativa, que são dados em Wolfowitz (1949). Como o poder, seja exato ou assintótico, pode ser calculado apenas para alternativas completamente especificadas, as comparações numéricas de potência não devem ser o único critério para este teste. Sua principal utilidade é em análises preliminares dos dados em que nenhuma forma particular de alternativa é formulada. Então, se a hipótese for rejeitada, estudos adicionais podem ser feitos com outros testes, na tentativa de classificar o tipo de diferença entre as populações.

III.2.2 Teste Kolmogorov-Smirnov para duas amostras

A estatística Kolmogorov-Smirnor é outro teste de uma amostra que pode ser adaptado ao problema de duas amostras. Lembre-se de que, como critério de bondade de ajuste, esse teste comparou a função de distribuição empírica de uma amostra aleatória com uma distribuição hipotética. No caso de duas amostras, a comparação é feita entre as funções de distribuição empíricas das duas amostras.

As estatísticas de ordem correspondentes a duas amostras aleatórias de tamanho \(m\) e \(n\) das populações contínuas \(F_X\) e \(F_Y\), são \begin{equation} X_{(1)}, X_{(2)}, \cdots, X_{(m)} \qquad \mbox{e} \qquad Y_{(1)}, Y_{(2)}, \cdots, Y_{(n)}\cdot \end{equation} Suas respectivas funções de distribuição empírica, denotadas por \(\widehat{F}_m(x)\) e \(\widehat{F}_n(x)\), são definidas como \begin{equation} \widehat{F}_m(x) \, = \, \left\{ \begin{array}{cccc} 0, & \mbox{se} & x < X_{(1)} & \\ \displaystyle\frac{k}{m}, & \mbox{se} & X_{(k)}\leq x < X_{(k+1)}, & k=1,2,\cdots,m-1 \\ 1, & \mbox{se} & x\geq X_{(m)} & \end{array}\right. \end{equation} e \begin{equation} \widehat{F}_n(x) \, = \, \left\{ \begin{array}{cccc} 0, & \mbox{se} & x < Y_{(1)} & \\ \displaystyle\frac{k}{n}, & \mbox{se} & Y_{(k)}\leq x < Y_{(k+1)}, & k=1,2,\cdots,n-1 \\ 1, & \mbox{se} & x\geq Y_{(n)} & \end{array}\right. \end{equation} Em um arranjo ordenado combinado das \(m+n\) observações amostrais, \(\widehat{F}_m(x)\) e \(\widehat{F}_n(x)\) são as respectivas proporções de observações \(X\) e \(Y\) que não excedem o valor especificado \(x\).

Se a hipótese nula \begin{equation} H_0 \, : \, F_Y(x) \, = \, F_X(x), \qquad \forall \, x \end{equation} é verdade, as distribuições populacionais são idênticas e temos duas amostras da mesma população.

As funções de distribuição empíricas para as amostras \(X\) e \(Y\) são estimativas razoáveis das respectivas funções de distribuição populacionais. Portanto, permitindo a variação da amostragem, deve haver concordância razoável entre as duas distribuições empíricas se, de fato, \(H_0\) for verdadeira. Caso contrário, os dados sugerem que \(H_0\) não é verdadeira e, portanto, deve ser rejeitada. Essa é a lógica intuitiva por trás da maioria dos testes de duas amostras e o problema é definir o que é uma concordância razoável entre as duas funções de distribuição empíricas. Em outras palavras, quão próximas as duas funções de distribuição empíricas devem estar, de modo que possam ser vistas como não significativamente diferentes, levando-se em consideração a variabilidade da amostragem. Note que esta abordagem requer necessariamente uma definição de proximidade. O critério de teste de duas amostras Kolmogorov-Smirnov bilateral, denotado por \(D_{m,n}\) é baseado na diferença absoluta máxima entre as duas distribuições empíricas \begin{equation} D_{m,n} \, = \, \max_x |\, \widehat{F}_m(x) \, - \, \widehat{F}_n(x) \, |\cdot \end{equation}

Uma vez que aqui apenas as grandezas, e não as direções dos desvios são consideradas, \(D_{m,n}\) é apropriado para uma alternativa geral bilateral \begin{equation} H_1 \, : \, F_Y(x) \, \neq \, F_X(x), \qquad \mbox{para algum } x \end{equation} e a região de rejeição está na cauda superior, definida por \(D_{m,n}\geq c_\alpha\), onde \(P(D_{m,n}\geq c_\alpha \, | \, H_0) \, \leq \, \alpha\).

Por causa do teorema de Gilvenko-Cantelli, o teste é consistente para esta alternativa. O \(p-valor\) é \begin{equation} P(D_{m,n}\geq D_0 \, | \, H_0), \end{equation} onde \(D_0\) é o valor observado da estatística do teste Kolmogorov-Smirnov de duas amostras. Como com a estatística de Kolmogorov-Smirnov de uma amostra, \(D_{m,n}\) é completamente de distribuição livre para qualquer distribuição contínua da população comum já que a ordem é preservada sob uma transformação monótona. Isso é, se fizermos \(z=F(x)\) para o função de distribuição \(F\) comum, temos \(\widehat{F}_m(z) \, = \, \widehat{F}_m(x)\) e \(\widehat{F}_n(z) \, = \, \widehat{F}_n(x)\), em que a variável aleatória \(Z\), correspondente para \(z\), tem distribuição uniforme no intervalo unitário.

A derivação da distribuição nula exata de \(D_{m,n}\) é geralmente atribuído à escola russa, particularmente Gnedenko (1954) e Korolyuk (1961), mas os artigos de Massey (1951, 1952) também são importantes. Vários métodos de cálculo são possíveis, geralmente envolvendo fórmulas recursivas. Drion (1952) derivou uma expressão fechada para probabilidades exatas no caso \(m = n\) aplicando técnicas de reamostragem. Diversas abordagens estão resumidas em Hodges (1958).

Para a distribuição nula assintótica, ou seja, \(m\) e \(n\) se aproximando ao infinito de tal forma que \(m/n\) permaneça constante, Smirnov (1939) provou que \begin{equation} \lim_{m,n\to\infty} P\Bigg( \sqrt{\frac{mn}{m+n}}D_{m,n}\leq d\Bigg) \, = \, L(d), \end{equation} onde \begin{equation} L(d) \, = \, 1-2\sum_{i=1}^\infty (-1)^{i-1} e^{-2i^2d^2}\cdot \end{equation}

Note que a distribuição assintótica de \(\sqrt{mn/(m+n)} \, D_{m,n}\) é exatamente a mesma que a distribuição assintótica de \(\sqrt{N} \, D_N\). Isso não é surpreendente, já que sabemos do teorema de Glivenco-Cantelli que, quando \(n \to \infty\), \(\widehat{F}_n(x)\) converge para \(F_Y(x)\), que pode ser remarcado como \(F_X(x)\). Então a única diferença aqui é no fator de normalização \(\sqrt{mn/(m+n)}\), que substitui \(\sqrt{N}\).

Os testes de Kolmogorov-Smirnov são fáceis de aplicar, usando a distribuição exata para quaisquer \(m\) e \(n\) dentro da faixa das tabelas disponíveis e usando a distribuição assintótica para amostras maiores. Eles são úteis principalmente para as alternativas gerais, uma vez que o teste estatístico é sensível a todos os tipos de diferenças entre as funções de distribuição. Sua aplicação principal deve ser para estudos preliminares de dados. Os testes de Kolmogorov-Smirnov são mais poderosos do que os testes de corridas quando comparados para grandes tamanhos de amostra.

III.2.3 O teste da mediana

Para testar a hipótese nula de populações idênticas com duas amostras independentes, o teste de duas amostras de Kolmogorov-Smirnov compara as proporções de observações de cada amostra que não excede um número \(x\) para todos os números reais \(x\). O critério do teste foi a diferença máxima absoluta ou unidirecional entre os duas distribuições empíricas, que são definidas para todos os \(x\). Suponha que em vez de usar todas as diferenças possíveis, escolhemos algumas arbitrárias mas num número específico \(\delta\) e comparamos apenas as proporções de observações de cada amostra que são estritamente menores que \(\delta\). Como antes, as duas amostras independentes são denotadas por \begin{equation} X_1, X_2, \cdots, X_m \qquad \mbox{e} \qquad Y_1,Y_2,\cdots,Y_n\cdot \end{equation}

Cada uma das \(m+n=N\) observações deve ser classificada de acordo se é menor que \(\delta\) ou não. Sejam \(U\) e \(V\) os respectivos números de observações \(X\) e \(Y\) menores que \(\delta\). Desde que as variáveis aleatórias em cada amostra foram dicotomizadas, \(U\) e \(V\) seguem a mesma distribuição binomial com parâmetros \begin{equation} p_X \, = \, P(X \, \le \, \delta) \qquad \mbox{e} \qquad p_Y \, = \, P(Y \, < \delta), \end{equation} e número de tentativas \(m\) e \(n\), respectivamente. Para duas amostras independentes, a distribuição conjunta de \(U\) e \(V\) é então \begin{equation} P(U=u, V=u) \, = \, {m \choose u}{n \choose v}p_X^u p_Y^v (1-p_X)^{m-u} (1-p_Y)^{n-v}, \end{equation} para \(u=0,1,\cdots,m\) e \(v=0,1,\cdots,n\).

As variáveis aleatórias \(U/m\) e \(V/n\) são estimativas pontuais não viciadas dos parâmetros \(p_X\) e \(p_Y\), respectivamente. A diferença \(U/m - V/n\) então é apropriada para testar a hipótese nula \begin{equation} H_0 \, : \, p_X - p_Y \, = \, 0\cdot \end{equation} A distribuição nula exata de \(U/m - V/n\) pode ser encontrada e, para \(m\) e \(n\) grandes, sua distribuição pode ser aproximada pelo normal. A estatística de teste em qualquer um dos casos depende no valor comum \(p = p_X = p_Y\), mas o teste pode ser realizado substituindo \(p\) por sua estimativa não viciada \((u+v)/(m+n)\). Caso contrário, não há dificuldade em construir um teste, embora aproximado, baseado no critério de diferença de proporções de observações menor que \(\delta\). Este é essencialmente um teste de sinal modificado para duas amostras independentes, com a hipótese de que \(\delta\) é o \(p\)-ésimo quantil em ambas as populações, onde \(p\) não é especificado, mas estimado a partir dos dados.

Este teste não será realizado aqui, uma vez que é aproximado e nem sempre é apropriado para o problema geral de duas amostras, onde estão principalmente interessados ​​na hipótese de populações idênticas. E se as duas populações são as mesmas, o \(p\)-ésimo quantil são iguais para todo valor de \(p\). No entanto, duas populações podem ser bastante díspares mesmo que alguns quantis sejam iguais. O valor de \(\delta\), que é supostamente escolhido sem o conhecimento das observações, afeta a sensibilidade do critério de teste. Se \(\delta\) for escolhido muito pequeno ou muito grande, tanto \(U\) quanto \(V\) terão um intervalo muito pequeno para serem confiáveis. Não podemos esperar ter poder razoável para o teste geral sem uma escolha judiciosa de \(\delta\). Um teste em que o experimentador escolhe um determinado valor de \(p\) em vez de \(\delta\), preferencialmente um valor central, seria mais apropriado para nossa hipótese geral, especialmente para detectar diferenças na locação. Em outras palavras, nós preferimos controlar a posição de \(\delta\), independentemente do seu valor real, mas \(p\) e \(\delta\) estão irremediavelmente inter-relacionados na população comum.

Quando as populações são consideradas idênticas mas não especificadas, não podemos escolher \(p\) e, em seguida, determinar o \(\delta\) correspondente. Ainda \(\delta\) deve ser conhecido pelo menos de forma posicional para classificar cada observação da amostra como menor do que \(\delta\) ou não. Portanto, suponha que decidimos controlar a posição de \(\delta\) em relação às magnitudes das observações da amostra. Se as quantidades \(U\) e \(V\) forem fixadas pelo experimentador antes da amostragem \(p\) é, até certo ponto, controlada desde que \((u+v)/(m+n)\) é uma estimativa de \(p\) comum. Se \(p\) denota a probabilidade de que qualquer observação seja menor que \(\delta\), a distribuição de \(T = U + V\) é \begin{equation} P(T=t) \, = \, {m+n \choose t} p^t (1-p)^{m+n-t}, \qquad t=0,1,2,\cdots, m+n\cdot \end{equation}

A distribuição condicional de \(U \, | \, T=t\) pode ser encontrada utilizando as expressões acima e, no caso nulo, quando \(p=p_X=p_Y\), temos por resultado \begin{equation} P_{U|T}(u \, | \, t) \, = \, \frac{\displaystyle {m \choose u}{n \choose t-u}}{\displaystyle {m+n \choose t}}, \qquad u=\max(0,t-n),1, \cdots,\max(m,t), \end{equation} a qual é a distribuição hipergeométrica. Esse resultado também poderia ter sido argumentado diretamente da seguinte forma. Cada uma das \(m+n\) observações é dicotomizada de acordo com \(\delta\), ou seja, se é menos ou não do que \(\delta\). Entre todas as observações, se \(p=p_X=p_Y\), cada um dos \({m+n \choose t}\) conjuntos de números de \(t\) números é igualmente susceptível de compreender o grupo dos menores do que \(\delta\).

O número de conjuntos que tem exatamente \(u\) elementos da amostra \(X\) é \({m \choose u}{n \choose t-u}\). Como \(U/m\) é uma estimativa de \(p_X\), se a hipótese \(p=p_X=p_Y\) for verdadeira, \(u/m\) deve estar perto de \(t/(m+n)\). Um critério de teste pode então ser encontrado usando a distribuição condicional de \(U\) para qualquer \(t\) escolhido.

O fato de que \(\delta\) não pode ser determinado antes que as amostras sejam obtidas pode ser perturbador, pois implica que \(\delta\) deve ser tratado como uma variável aleatória. Ao derivar a distribuição condicional de \(U|T\) tratamos \(\delta\) como uma constante, mas o mesmo resultado é obtido para \(\delta\) definido como a mediana da amostra. Vamos denotar por \(Z\) a mediana da amostra combinada e por \(F_X\) e \(F_Y\) as funções de distribuição de \(X\) e \(Y\), respectivamente, e assumamos que \(N\) seja ímpar. A mediana \(Z\) pode ser uma das variáveis aleatórias \(X\) ou \(Y\), e essas possibilidades são mutuamente exclusivas. A função de densidade conjunta de \(U\) e \(Z\) para \(t\) observações menores que a mediana amostral onde \(t=(N-1)/2\) é o limite, quando \(\Delta z\) se aproxima de zero, da soma de as probabilidades de que (1) os \(X\) estão divididos em três classificações, \(u\) menores que \(z\), um entre \(z\) e \(z+\Delta z\) e os restantes maiores que \(z+\Delta z\) e os \(Y\) são divididos de tal forma que \(t-u\) são menores que \(z\) e (2) exatamente \(u\) dos \(X\) sejam menores que \(z\) e os \(Y\) sejam divididos de tal forma que \(t-u\) sejam menores que \(z\), um entre \(z\) e \(z+\Delta z\) e os restantes sejam maiores que \(z+\Delta z\). O resultado então é \begin{equation} \begin{array}{rcl} f_{U,Z}(u,z) & = & \displaystyle {m \choose u,1,m-1-u} F_X^u(z)f_X(z)\big(1-F_X(z)\big)^{m-1-u}{n \choose t-u}F_Y^{t-u}(z) \big(1-F_Y(z)\big)^{n-t+u} \, + \\ & & \displaystyle \, + \, {m \choose u}F_X^u(z)\big(1-F_X(z)\big)^{m-u}{n \choose t-u,1,n-t+u-1}^{t-u}F_Y^{t-u}(z)f_Y(z)\big(1-F_Y(z)\big)^{m-t+u-1}\cdot \end{array} \end{equation}

A densidade marginal de \(U\) é obtida pela integração da expressão sobre todo \(z\) e, se \(F_X(z)=F_Y(z)\) para todo \(z\), o resultado é \begin{equation} \begin{array}{rcl} f_U(u) & = & \displaystyle \left( m{m-1 \choose u}{n \choose t-u}+n{m \choose u}{n-1 \choose t-u}\right)\int_{-\infty}^\infty F^t(z)\big(1-F(z)\big)^{m+n-t-1}f(z)\mbox{d}z \\ & = & \displaystyle{m \choose u}{n \choose t-u}\big( (m-u)+(n-t+u)\big)Beta(t+1,m+n-t) \, = \, {m \choose u}{n \choose t-u} \frac{t! (m+n-t)!}{(m+n)!}\cdot \end{array} \end{equation}

Por causa desse resultado podemos dizer que antes da amostragem, ou seja, antes que o valor de \(\delta\) seja determinado, a estatística do teste da mediana é apropriado para a hipótese geral de populações iêênticas, e depois que as amostras ão obtidas, a hipótese testada é que \(\delta\) seja \(p\)-ésimo quantil em ambas as populações, onde \(p\) é um número próximo a 0.5. As distribuições nulas da estatística de teste são as mesmas para ambas hipóteses, no entanto.

Embora a discussão anterior possa implicar que o teste da mediana tenha algumas limitações estatísticas e filosóficas na concepção, é bem conhecido e aceito dentro do contexto do problema geral amostral. O procedimento para duas amostras de medições independentes consiste em organizar as amostras combinadas em ordem crescente de magnitude e determinar a mediana amostral \(\delta\), a observação com classificação \((N+1)/2\) se \(N\) é ímpar e qualquer número entre as observações com classificações \(N/2\) e \((N+2)/2\) se \(N\) é par. Um total de \(t\) observações é então menor que \(\delta\), onde \(t=(N-1)/2\) ou \(N/2\) conforme \(N\) é ímpar ou par. Seja \(U\) o número de observações \(X\) menores que \(\delta\). Se as duas amostras são extraídas de populações contínuas idênticas, a função de probabilidade de \(U\) para \(t\) fixo é \begin{equation} f_U(u) \, = \, \frac{\displaystyle {m \choose u}{n \choose t-u}}{\displaystyle {m+n \choose t}} \end{equation} onde \(u=\max(0,t-n), \cdots,\min(m,t)\), \(t=[N/2]\) sendo que \([x]\) denota o maior número inteiro que não excede o valor \(x\). Se a hipótese nula é verdadeira, então \(P(X < \delta)= P(Y< \delta)\) para todos os \(\delta\), e em particular as duas populações têm mediana comum, que é estimada por \(\delta\).

Como \(U/m\) é um estimador de \(P(X <\delta)\), que é aproximadamente metade sob \(H_0\), um teste baseado no valor de \(U\) será mais sensível a diferenças de locação. Se \(U\) for muito maior que \(m/2\), a maior parte dos valores de \(X\) serão menores do que a maioria dos valores de \(Y\). Isso dá credibilidade à relação \(P(X <\delta)> P(Y <\delta)\), que são os \(X\) estocasticamente menores que os \(Y\), de modo que a mediana da população \(X\) é menor que a mediana da população \(Y\), ou que \(\theta> 0\). Se \(U\) é muito pequena em relação a \(m/2\), a conclusão oposta está implícita. As regiões de rejeição apropriadas e os \(p\)-valores para o nível de significância nominal são então os seguintes:

Os valores críticos \(c\) e \(c_0\) podem ser facilmente encontrados utilizando a função de densidade \(f_U\), utilizando a distribuição hipergeométrica ou usando coeficientes binomiais. Se \(N\) é par, nossa escolha é \(c'_\alpha=m-c_\alpha\). Como a distribuição \(f_U\) não é simétrica para \(m\neq n\) se \(N\) for ímpar, a escolha de uma região de rejeição ótima para um teste bilateral não está claro para este caso. Poderia ser escolhido de tal forma que \(\alpha\) seja dividido igualmente ou que o intervalo de \(u\) seja simétrico, ou nenhum dos dois.

Se \(m\) e \(n\) forem tão grandes que o cálculo para encontrar valores críticos não é viável, uma aproximação normal à distribuição hipergeométrica pode ser usada. Usando fórmulas para a média e a variância da distribuição hipergeométrica e a distribuição \(f_U\), a média e a variância de \(U\) são encontradas como sendo \begin{equation} \mbox{E}(U \, | \, t) \, = \, \dfrac{mt}{N} \qquad \mbox{e} \qquad \mbox{Var}(U \, | \, t) \, = \, \dfrac{mnt(N-t)}{N^2(N-1)}\cdot \end{equation}

Se \(m\) e \(n\) crecerem ao infinito de tal forma que \(m/n\) permaneça constante, esta distribuição hipergeométrica se aproxima da distribuição binomial para \(t\) tentativas com parâmetro \(m/N\), que por sua vez se aproxima a distribuição normal. Para \(N\) grande, a variância de \(U\) é aproximadamente \begin{equation} \mbox{Var}(U \, | \, t) \, = \, \dfrac{mnt(N-t)}{N^3} \end{equation} e assim a distribuição assintótica de \begin{equation} Z \, = \, \dfrac{\displaystyle U-\frac{mt}{N}}{\displaystyle \sqrt{\frac{mnt(N-t)}{N^3}}} \end{equation} é aproximadamente normal padrão. Uma correção de continuidade de 0.5 pode ser utilizada para melhorar a aproximação. Por exemplo, quando a alternativa é \(\theta < 0\) ou \(M_Y < M_X\), o \(p\)-valor aproximado com uma correção de continuidade é dado por \begin{equation} \Phi\left( \dfrac{U_0+0.5-mt/N}{\sqrt{mnt(N-t)/N^3}}\right)\cdot \end{equation}

III.2.4 Teste \(U\) de Mann-Whitney

Como o teste de corridas de Wald-Wolfowitz, o teste \(U\) de Mann-Whitney (Mann and Whitney, 1947) baseia-se na ideia de que o padrão particular exibido quando as variáveis aleatórias \(X\) e \(Y\) estão dispostas juntas em ordem crescente de magnitude fornece informações sobre a relação entre suas populações. No entanto, em vez de medir a tendência de agrupar pelo número total de corridas, o critério de Mann-Whitney é baseado nas magnitudes de, digamos, os \(Y\) em relação aos \(X\), ou seja, a posição dos \(Y\) na sequência combinada ordenada. Um padrão de arranjo de amostra onde a maioria dos \(Y\) é maior que a maioria dos \(X\) ou vice-versa, ou ambos seria uma evidência contra uma mistura aleatória e, assim, tenderia a desacreditar a hipótese nula de distribuições idênticas.

A estatística do teste \(U\) de Mann-Whitney é definida como o número de vezes que um \(Y\) precede um \(X\) no arranjo ordenado combinado das duas amostras aleatórias independentes \begin{equation} X_1, X_2, \cdots, X_m \qquad \mbox{e} \qquad Y_1, Y_2, \cdots, Y_n \end{equation} em uma única sequência de \(m + n = N\) variáveis aumentando em magnitude. Assumimos que as duas amostras são extraídas de distribuições contínuas, de modo que a possibilidade de que \(X_i = Y_j\) para alguns \(i\) e \(j\) não precisa ser considerada. Se as \(mn\) variáveis aleatórias indicadoras forem definidas como \begin{equation} D_{ij} \, = \, \left\{ \begin{array}{ccl} 1, & \mbox{se} & Y_j < X_i, \quad i=1,2,\cdots,m; \; j=1,2,\cdots,n \\ 0, & \mbox{se} & Y_j > X_i \end{array}\right. \end{equation} a representação simbólica da estatística \(U\) de Mann-Whitney é \begin{equation} U \, = \, \sum_{i=1}^m \sum_{j=1}^n D_{ij}\cdot \end{equation}

A região de rejeição lógica para a alternativa unilateral que os \(Y\) são estocasticamente maiores que os \(X\), \begin{equation} H_1 \, : \, F_Y(x)\, \leq \, F_X(x), \end{equation} com a desigualdade estrita para alguns \(x\), seria claramente valores pequenos de \(U\). O fato de que este é um critério de teste consistente pode ser mostrado investigando a convergência de \(U/mn\) para um determinado parâmetro onde \(H_0\) pode ser escrito como uma declaração sobre o valor desse parâmetro.

Para esse propósito, definimos \begin{equation} p \, = \, P(Y \, < \, X) \, = \, \int_{-\infty}^\infty \int_{-\infty}^\infty f_Y(y)f_X(x)\mbox{d}y\mbox{d}x \, = \, \int_{-\infty}^\infty F_Y(x)\mbox{d}F_X(x) \end{equation} e o problema do teste de hipóteses pode ser redefinido em termos do parâmetro \(p\). Se \(H_0 \, : \, F_Y(x)=F_X(x)\) para todo \(x\) for verdadeira, então \begin{equation} p \, = \, \int_{-\infty}^\infty F_X(x)\mbox{d}F_X(x) \, = \, 0.5\cdot \end{equation} Se, por exemplo, a hipótese alternativa for \(H_1 \, : \, F_Y(x)\leq F_X(x)\), isto é, \(Y\stackrel{\text{ST}}{>}X\), então \(H_1 \, : \, p\leq 0.5\) para todo \(x\) e \(p < 0.5\) para algum \(x\). Assim, a hipótese nula de distribuições idênticas pode ser parametrizada para \(H_0 \, : \, p=0.5\) e a hipótese alternativa para \(H_1 \, : \, p < 0.5\).

As \(mn\) variáveis aleatórias indicadoras são variáveis Bernoulli com momentos \begin{equation} \mbox{E}(D_{ij}) \, = \, \mbox{E}(D_{ij}^2) \, = \, p \qquad \mbox{e} \qquad \mbox{Var}(D_{ij}) \, = \, p(1-p)\cdot \end{equation} Para os momentos de conjuntos, notamos que essas variáveis aleatórias não são independentes sempre que os subscritos \(X\) ou os subscritos \(Y\) são comuns, de modo que \begin{equation} \mbox{Cov}(D_{ij},D_{hk}) \, = \, 0 \qquad \mbox{para } i\neq h \quad \mbox{e} \quad j\neq k \end{equation} e \begin{equation} \mbox{Cov}(D_{ij},D_{ik}) \, = \, p_1-p^2 \qquad \mbox{para } j\neq k \qquad \mbox{e} \qquad \mbox{Cov}(D_{ij},D_{hj}) \, = \, p_2-p^2 \qquad \mbox{para } i\neq h, \end{equation} sendo que os parâmetros adicionais introduzidos são \begin{equation} p_1 \, = \, P(Y_j < X_i \, \cap \, Y_k < X_i) \, = \, P(Y_j \; \mbox{e} \; Y_k < X_i) \, = \, \displaystyle \int_{-\infty}^\infty F_y^2(x)\mbox{d}F_X(x) \end{equation} e \begin{equation} p_2 \, = \, P(X_i > Y_j \, \cap \, X_h > Y_j) \, = \, P(X_i \; \mbox{e} \; X_h > Y_j) \, = \, \displaystyle \int_{-\infty}^\infty \big(1-F_X(y)\big)^2\mbox{d}F_Y(y)\cdot \end{equation}

Como \(U\) foi definida como uma combinação linear de \(mn\) variáveis aleatórias, a média e variância de \(U\) são \begin{equation} \mbox{E}(U) \, = \, \sum_{i=1}^m \sum_{j=1}^n \mbox{E}(D_{ij}) \, = \, mnp, \end{equation} e \begin{equation} \begin{array}{rcl} \mbox{Var}(U) & = & \displaystyle \sum_{i=1}^m \sum_{j=1}^n \mbox{Var}(D_{ij}) \, + \, \sum_{i=1}^m \underset{1 \, \leq \, j \, \neq \, k \, \leq \, n}{\sum\sum} \mbox{Cov}(D_{ij},D_{ik}) \, + \, \sum_{j=1}^n \underset{1 \, \leq \, i \, \neq \, h \, \leq \, m}{\sum\sum} \mbox{Cov}(D_{ij},D_{hj}) \, + \, \\ & & \qquad + \displaystyle \, \underset{1 \, \leq \, i \, \neq \, h \, \leq \, m}{\sum\sum} \underset{1 \, \leq \, j \, \neq \, k \, \leq \, n}{\sum\sum} \mbox{Cov}(D_{ij},D_{hk}) \cdot \end{array} \end{equation}

Substituindo os valores correspondentes à variância, temos que \begin{equation} \begin{array}{rcl} \mbox{Var}(U) & = & mnp(1-p)+mn(n-1)(p_1-p^2)+nm(m-1)(p_2-p^2) \\ & = & mn\big( p-p^2(N-1)+(n-1)p_1+(m-1)p_2\big)\cdot \end{array} \end{equation} Sabemos que \(\mbox{E}(U/mn)=p\) e que \(\displaystyle \lim_{m,n\to\infty} \mbox{Var}(U/mn)=0\), do qual concluímos que \(U/mn\) é um estimador consistente de \(p\). Com bases nestes resultados o teste de Mann-Whitney é consistente nas seguintes situações:

Para determinar o tamanho \(\alpha\) das regiões críticas do teste de Mann-Whitney, devemos agora encontrar a distribuição de probabilidade nula de \(U\). Sob \(H_0\), cada um dos \(\displaystyle {m+n \choose m}\) arranjos das variáveis aleatórias em uma sequência combinada ocorre com igual probabilidade, de modo que \begin{equation} f_U(u) \, = \, P(U \, = \, u) \, = \, \dfrac{r_{m,n}(u)}{\displaystyle {m+n \choose m}}, \end{equation} onde \(r_{m,n}(u)\) é o número de arranjos distinguíveis das \(m\) variáveis aleatórias \(X\) e \(n\) variáveis aleatórias \(Y\), de modo que em cada sequência o número de vezes que um \(Y\) precede um \(X\) é exatamente \(u\). Os valores de \(u\) para os quais \(f_U(u)\) é diferente de zero entre zero e \(mn\), para as duas ordenações mais extremas em que cada \(x\) precede cada \(y\) e todo \(y\) precede cada \(x\), respectivamente. Primeiro notamos que a distribuição de probabilidade de \(U\) é simétrica em relação à média \(mn/2\) sob a hipótese nula. Esta propriedade pode ser discutida da seguinte forma. Para cada disposição particular \(z\) das \(m\) letras \(x\) e as \(n\) letras \(y\), defina o arranjo conjugado \(z'\) como a sequência \(z\) escrita para trás. Em outras palavras, se \(z\) denota um conjunto de números escritos do menor para o maior para o maior, \(z'\) denota os mesmos números escritos do maior para o menor. Todo \(y\) que precede um \(x\) em \(z\) segue então aquele \(x\) em \(z'\), de modo que se \(u\) é o valor da estatística de Mann-Whitney para \(z\), \(mn-u\) é o valor para \(z'\). Portanto, sob \(H_0\) temos, \begin{equation} \begin{array}{rcl} \displaystyle P\Big( U-\frac{mn}{2} \, = \, u \Big) & = & \displaystyle P\Big( U \, = \, \frac{mn}{2} + u \Big) \\ & = & \displaystyle P\Big( U \, = \, mn - \big(\frac{mn}{2} + u\big) \Big) \, = \, P\Big( U-\frac{mn}{2} \, = \, -u \Big)\cdot \end{array} \end{equation}

Devido a essa propriedade de simetria, somente os valores críticos da cauda inferior precisam ser encontrados para um teste de um ou dois lados. Definimos a variável aleatória \(U'\) como o número de vezes que um \(X\) precede um \(Y\) ou \begin{equation} U' \, = \, \sum_{i=1}^m\sum_{j=1}^n (1-D_{ij}) \end{equation} e redefinimos as regiões de rejeição para testes de tamanho \(\alpha\) correspondentes ao seguinte:

Para determinar o número \(c_\alpha \) para qualquer \(m\) e \(n\), podemos enumerar os casos começando com \(u = 0 \) e trabalhar até que, pelo menos, \(\alpha {m+n \choose m}\) casos sejam contados. Por exemplo, para \(m = 4 \), \(n = 5 \), os arranjos com os menores valores de \(u\), isto é, onde a maior parte do \(X\) é menor que a maior parte do \(Y\), são mostrados na Tabela abaixo. As regiões de rejeição para este teste unilateral para níveis de significância nominal de 0.01 e 0.05 seriam então \(U \leq 0 \) e \(U \leq 2 \), respectivamente.

Embora seja relativamente fácil adivinhar quais ordenamentos levarão aos menores valores de \(u\), \({m + n \choose m}\) aumenta rapidamente à medida que \(m\) e \(n\) aumentam. Algum método mais sistemático de geração de valores críticos é necessário para eliminar a possibilidade de ignorar alguns arranjos com \(u\) pequeno e aumentar a faixa viável de tamanhos de amostras e níveis de significância. Uma relação de recorrência particularmente simples e útil pode ser derivada para a estatística de Mann-Whitney. Considere uma sequência de \(m + n\) letras sendo construídas adicionando uma letra à direita de uma sequência de \(m + n-1\) letras. Se as \(m + n-1\) letras consistirem em \(m\) letras \(x\) e \(n-1\) letras \(y\), a letra extra deve ser \(y\). Mas se \(y\) for adicionado à direita, o número de vezes que \(y\) precede um \(x\) não é alterado. Se a letra adicional é um \(x\), o que seria o caso das \(m-1\) letras \(x\) e \(n\) letras \(y\) na sequência original, todos os \(y\) precedem este novo \(x\) e há \(n\) deles, de modo que \(u\) é aumentado por \(n\). Essas duas possibilidades são mutuamente exclusivas. Usando a notação do numerador em \(f_U\) novamente, esta relação de recorrência pode ser expressa como \begin{equation} r_{m,n}(u) \, = \, r_{m,n-1}(u) \, + \, r_{m-1,n}(u-n) \end{equation} e \begin{equation} \begin{array}{rcl} f_U(u) & = & p_{m,n}(u) \, = \, \displaystyle \dfrac{r_{m,n-1}(u) \, + \, r_{m-1,n}(u-n)}{{m+n \choose m}} \\ & = & \displaystyle \frac{n}{m+n}\frac{r_{m,n-1}(u)}{{m+n-1 \choose n-1}} \, + \, \frac{m}{m+n}\frac{r_{m-1,n}(u-n)} {{m+n-1 \choose m-1}} \end{array} \end{equation} ou \begin{equation} (m+n)p_{m,n}(u) \, = \, np_{m,n-1}(u) \, + \, p_{m-1,n}(u-n)\cdot \end{equation}

Esta relação recursiva vale para todos os \(u=0,1,2,\cdots,mn\) e todos valores inteiros \(m\) e \(n\) se as seguintes condições iniciais e de fronteira forem definidas para todos \(i=1,2,\cdots,m\) e \(j=1,2,\cdots,n\): \begin{equation} \begin{array}{rcc} r_{ij}(u) \, = \, 0, & \mbox{para todo} & u < 0, \\ r_{i0}(0) \, = \, 1, & \mbox{e} & r_{0,i}(0) \, = \, 1, \\ r_{i,0}(u) \, = \, 0, & \mbox{para todo} & u\neq 0, \\ r_{0,i}(u) \, = \, 0, & \mbox{para todo} & u\neq 0\cdot \end{array} \end{equation}

Quando \(m\) e \(n\) são grandes as distribuição assintótica pode ser usada. Como \(U\) é a soma de variáveis aleatórias distribuídas identicamente, embora dependentes, uma generalização do Teorema Central do Limite nos permite concluir que a distribuição nula de \(U\) padronizada se aproxima da normal padrão quando \(m,n\to\infty\) de tal maneira que \(m/n\) permanece constante (Mann & Whitney, 1947). Para fazer uso dessa aproximação, a média e a variância de \(U\) sob a hipótese nula deve ser determinada. Obtemos assim que \begin{equation} \mbox{E}(U \, | \, H_0) \, = \, \frac{mn}{2} \qquad \mbox{e} \qquad \mbox{Var}(U \, | \, H_0) \, = \, \frac{mn(N+1)}{2}\cdot \end{equation} A estatística de teste em amostras grandes é então \begin{equation} Z \, = \, \frac{U-mn/2}{\sqrt{mn(N+1)/12}}, \end{equation} cuja distribuição é aproximadamente normal padrão. Esta aproximação foi encontrada razoavelmente precisa para tamanhos de amostra iguais tão pequenos quanto 6. Como \(U\) pode assumir apenas valores inteiros, uma correção de continuidade de 0.5 pode ser usada.

III.3 Medidas de Associação em Classificações Múltiplas

Suponha que temos um conjunto de dados completo com \(I\) linhas e \(J\) colunas, com uma entrada em cada uma das \(I\times J\) células. Sob a hipótese nula de populações idênticas, os dados podem ser considerados como uma única amostra aleatória de tamanho \(IJ\) da população comum. O paralelo a este problema na estatística clássica é a Anáálise Variância. Vamos estudar alguns procedimentos análogos não paramétricos à Análise de Variância tudo paralelo, no sentido de que os dados são apresentados na mesma forma.

Vamos primeiro revisar as técnicas da Análise de Variância, abordagem para testar a hipótese nula de que os efeitos são todos o mesmo. O modelo é geralmente escrito \begin{equation} X_{ij} \, = \, \mu + \beta_i + \theta_j + \epsilon_{ij}, \qquad \mbox{para} \quad i=1,2,\cdots,I \quad \mbox{e} \quad j=1,2,\cdots,J\cdot \end{equation} Os termos \(\beta_i\) e \(\theta_j\) são conhecidos como os efeitos por fila e columa, respectivamente. No modelo teórico, os erros \(\epsilon_{ij}\) são variáveis aleatórias independentes, normalmente distribuídas com média zero e variância \(\sigma^2_\epsilon\). A estatística de teste para a hipótese nula de efeitos de coluna iguais ou, equivalentemente, \begin{equation} H_0: \, \theta_1=\theta_2=\cdots=\theta_J, \end{equation} é a relação \begin{equation} \frac{(I-1)\displaystyle \sum_{j=1}^J (\overline{X}_j-\overline{X})^2} {\displaystyle \sum_{i=1}^I\sum_{j=1}^J (X_{ij}-\overline{X}_I-\overline{X}_j+\overline{X})^2}, \end{equation} onde \begin{equation} \overline{X}_i=\frac{1}{J}\sum_{j=1}^JX_{ij}, \qquad \overline{X}_j=\frac{1}{I}\sum_{i=1}^IX_{ij} \qquad \mbox{e} \qquad \overline{X}=\frac{1}{IJ}\sum_{i=1}^I\sum_{j=1}^JX_{ij}\cdot \end{equation} Se todas as suposições do modelo forem atendidas, esta estatística de teste tem distribuição \(F-Fisher\) com graus de liberdade \(J-1\) e \((I-1)(J-1)\).

Os dois primeiros paralelos deste desenho que consideraremos são os problemas de \(k\)-amostras relacionadas problemas e o de \(k\)-amostras combinadas. A correspondência pode surgir de duas maneiras diferentes, mas ambas são de certa forma análogas aos modelos de blocos randomizados. Nestes modelos, as \(IJ\) unidades experimentais são agrupadas em \(I\) blocos, cada um contendo \(J\) unidades. Um conjunto de \(J\) tratamentos são atribuídos aleatoriamente &agravs;s unidades dentro de cada bloco de tal forma que todas as \(J\) observações sejam igualmente prováveis e as observações em blocos diferentes sejam independentes. O esquema de agrupamento em blocos é importante, uma vez que o propósito de tal projeto é minimizar as diferenças entre as unidades no mesmo bloco. Se o projeto for bem sucedida, as estimativas do erro experimental podem ser obtidas sem a perturbação atribuída às diferenças entre blocos. Este modelo é frequentemente apropriado na experimentação agrícola, desde que os efeitos da um possível gradiente de fertilidade pode ser reduzido. Dividindo o campo em \(I\) blocos, os gráficos dentro de cada bloco podem ser mantidos próximos. Quaisquer diferenças entre parcelas dentro do mesmo bloco podem ser atribuídas a diferenças entre os tratamentos e o efeito de bloco pode ser eliminado da estimativa do erro experimental.

O primeiro problema de amostras relacionadas surge onde os \(IJ\) sujeitos são agrupados em \(I\) blocos cada um contendo \(J\) observações relacionadas e dentro cada bloco \(J\) tratamentos são realizados aleatoriamente aos sujeitos relacionados. Os efeitos dos tratamentos são observados e denotamos por \(X_{ij}\) as observações no \(i\)-ésimo bloco do tratamento número \(j\), \(i=1,2,\cdots,I\) e \(j=1,2,\cdots,J\). Como as observações em diferentes blocos são independentes, a coleção de observações na \(j\)-ésima coluna são independentes. Para determinar se o efeito dos tratamentos são todos iguais, o teste de Análise de Variância é apropriado se as suposições necessárias são justificadas. Se as observações em cada linha \(X_{i1},X_{i2},\cdots,X_{iJ}\) são substituídas por sua classificação nessa linha, um teste não paramétrico envolvendo as somas por coluna é a Análise de Variância por postos de Friedman. A hipótese nula é que os efeitos dos tratamentos são todos iguais ou \begin{equation} H_0: \, \theta_1 \, = \, \theta_2 \, = \, \cdots \, = \, \theta_J \end{equation} e a alternativa para o teste de Friedman é \begin{equation} H_1: \, \theta_i \neq \theta_j, \qquad \mbox{para, pelo menos, um} \quad i\neq j\cdot \end{equation}

III.3.1 Extensão do teste da mediana

Sob a hipótese de populações idênticas, temos uma única amostra aleatória de tamanho \(\sum_{i=1}^k n_i=N\) da população comum. A mediana geral \(\delta\) das amostras agrupadas é uma estimativa da mediana dessa população comum. Portanto, uma observação de qualquer uma das \(k\) amostras é tão provável que seja acima de \(\delta\) como abaixo dela. O conjunto de \(N\) observações apoiará a hipótese nula se, para cada uma das \(k\) amostras, cerca de metade das observações nessa amostra forem inferiores à mediana da grande amostra. Um teste baseado neste critério é atribuído a Mood (1950) e Brown & Mood (1948, 1951).

Como no caso de duas amostras, a mediana geral \(\delta\) será definida como a observação na amostra ordenada agrupada que tem classificação \((N+1)/2\) se \(N\) for ímpar e qualquer número entre as duas observações com postos \(N/2\) e \((N+2)/2\) se \(N\) é par. Então, para cada amostra separadamente, as observações são dicotomizadas de acordo como são menores que \(\delta\) ou não. Defina a variável aleatória \(U_i\) como o número de observações na amostra \(i\) que são menores que \(\delta\) e seja \(t\) o número total de observações que são menores que \(\delta\). Então, pela definição de \(\delta\), temos \begin{equation} t \, = \, \displaystyle\sum_{i=1}^k u_i \, = \, \left\{ \begin{array}{cc} N/2 & \mbox{ caso } N \mbox{ seja par} \\ (N-1)/2 & \mbox{ caso } N \mbox{ seja ímpar}\end{array}\right.\cdot \end{equation}

Considerando \(u_i\) denotar o valor observado de \(U_i\), podemos apresentar os cálculos na tabela a seguir.

Sob a hipótese nula, cada um dos \({N \choose t}\) possíveis conjuntos de \(t\) observações tem a mesma probabilidade de estar na categoria menor que \(\delta\) e o número de dicotomizações com este resultado amostral particular é \(\prod_{i=1}^k {n_i \choose u_i}\). Portanto, a distribuição de probabilidade nula das variáveis aleatórias é a extensão multivariada da distribuição hipergeométrica ou \begin{equation} f(u_1,u_2,\cdots,u_k \, | \, t) \, = \, {n_1 \choose u_1}{n_2 \choose u_2}\cdots{n_k \choose u_k} \, \Big/ \, {N \choose t}\cdot \end{equation}

Se algum ou todos os \(U_i\) diferirem muito de seu valor esperado de \(n_i \theta\), onde \(\theta\) denota a probabilidade de que uma observação da população comum seja menor que \(\delta\), a hipótese nula poderia ser rejeitada. Geralmente, seria impreciso configurar regiões de rejeição de junção para as estatísticas de teste \(U_1,U_2,\cdots,U_k\), devido à grande variedade de combinações dos tamanhos de amostra \(n_1,n_2,\cdots,n_k\) e ao fato de que a hipótese alternativa é geralmente bilateral para \(k> 2\), como no caso do teste \(F\). Felizmente, podemos usar outro critério de teste que, embora seja uma aproximação, é razoavelmente preciso, mesmo para \(N\) tão pequeno quanto 25, se cada amostra consistir em pelo menos cinco observações. Esta estatística de teste pode ser derivada apelando para a análise do teste de bondade de ajuste. Cada um dos \(N\) elementos da amostra agrupada é classificado de acordo com dois critérios, o número da amostra e sua magnitude em relação a \(\delta\). Sejam estas \(2k\) categorias denotas por \((i,j)\), onde \(i=1,2,\cdots,k\) de acordo com número da amostra e \(j=1\) se a observação é menor do que \(\delta\) e \(j=2\) caso contrário. Vamos denotar as frequências esperadas para a \((i,j)\) categoria por \(f_{ij}\) e \(e_{ij}\), respectivamente. Então \begin{equation} f_{i1} \, = \, u_i, \qquad f_{i2} \, = \, n_i-u_i, \qquad \mbox{para } \, i=1,2,\cdots,k\cdot \end{equation} e as frequências esperadas quando \(H_0\) é verdadeira estimadas dos dados como \begin{equation} e_{i1} \, = \, \dfrac{n_it}{N}, \qquad e_{i2} \, = \, \dfrac{n_i(N-t)}{N}, \qquad \mbox{para } \, i=1,2,\cdots,k\cdot \end{equation}

O teste da bondade de ajuste para essas \(2k\) categorias é então \begin{equation} \begin{array}{rcl} Q & = & \displaystyle\sum_{i=1}^k\sum_{j=1}^2 \dfrac{(f_{ij}-e_{ij})^2}{e_{ij}} \\ & = & \displaystyle \sum_{i=1}^k \dfrac{(u_i-n_it/N)^2}{n_it/N} \, + \, \sum_{i=1}^k \dfrac{\big(n_i-u_i-n_i(N-t)/N \big)^2}{n_i(N-t)/N} \\ & = & \displaystyle N\sum_{i=1}^k \dfrac{(u_i-n_it/N)^2}{n_it} \, + \, N\sum_{i=1}^k \dfrac{\big(n_i-u_i-n_i(N-t)/N \big)^2}{n_i(N-t)} \\ & = & \displaystyle N\sum_{i=1}^k \dfrac{(u_i-n_it/N)^2}{n_i}\Big( \dfrac{1}{t}+\dfrac{1}{N-t}\big) \\ & = & \displaystyle \dfrac{N^2}{t(N-t)}\sum_{i=1}^k \dfrac{(u_i-n_it/N)^2}{n_i} \end{array} \end{equation} e \(Q\) tem aproximadamente distribuição do qui-quadrado sob \(H_0\). Os parâmetros estimados a partir dos dados são as \(2k\) probabilidades de que uma observação seja menor que \(\delta\) para cada uma das \(k\) amostras e que não sejam menores que \(\delta\). Mas, para cada amostra, essas probabilidades somam 1 e, portanto, há apenas \(k\) parâmetros independentes estimados. O número de graus de liberdade para \(Q\) é então \(2k-1-k\) ou \(k-1\). A aproximação qui-quadrado para a distribuição de \(Q\) é um pouco melhorada pela multiplicação de \(Q\) pelo fator \((N-1)/N\). Então a região de rejeição é \begin{equation} Q \, \in \, \mathbb{R} \qquad \mbox{para} \qquad \dfrac{(N-1)Q}{N} \, \geq \, \chi^2_{k-1,\alpha}\cdot \end{equation}

Assim como no teste de mediana de duas amostras, as observações empatadas não apresentam um problema a menos que haja mais de uma observação igual à mediana, que pode ocorrer apenas para \(N\) ímpar ou se \(N\) é par e as duas observações médias são iguais. Sugere-se a abordagem conservadora, segundo a qual a decisão é baseada nessa resolução de vínculos que leva ao menor valor de \(Q\).

III.3.2 Análise de Variância por postos de Friedman

Neste modelo a amostra será apresentada sob a forma de uma tabela com \(k\) linhas e \(n\) colunas. As linhas indicam números de bloco, assunto ou amostra e as colunas são efeitos do tratamento. As observações em diferentes linhas são independentes, mas as colunas não são por causa de alguma unidade de associação. Para evitar fazer as suposições necessárias para o teste usual de análise de variância de que os \(n\) tratamentos são os mesmos, Friedman (1937, 1940) sugeriu substituir cada observação de tratamento dentro do \(i\)-bloco por um número do conjunto \(\{1,2,\cdots,n\}\) que representa a magnitude do tratamento em relação às outras observações no mesmo bloco. Denotamos as observações ranqueadas por \(R_{ij}\), \(i=1,2,\cdots,k\), \(j=1,2,\cdots,n\) de modo que \(R_{ij}\) é o posto do \(j\)-ésimo efeito do tratamento no \(i\)-ésimo bloco. Então \(R_{i1},R_{i2}\cdots,R_{in}\) é uma permutação dos primeiros \(n\) inteiros e \(R_{1j},R_{2j},\cdots,R_{kj}\) o conjunto de postos dados ao \(j\)-ésimo efeito do tratamento em todos os blocos. Representamos os dados em forma de tabela da seguinte forma: \begin{equation} \begin{array}{cccccc} & 1 & 2 & \cdots & n & \mbox{Totais por linha} \\ 1 & R_{11} & R_{12} & \cdots & R_{1n} & n(n+1)/2 \\ 2 & R_{21} & R_{22} & \cdots & R_{2n} & n(n+1)/2 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ k & R_{k1} & R_{k2} & \cdots & R_{kn} & n(n+1)/2 \\ \mbox{Totais por coluna} & R_1 & R_2 & \cdots & R_n & kn(n+1)/2 \end{array} \end{equation}

Os totais das linhas são constantes, mas os totais das colunas são afetados pelas diferenças entre os efeitos do tratamento. Se os efeitos do tratamento forem todos iguais, cada coluna esperada é igual e igual a média da coluna dos totais \(k(n+1)/2\). A soma dos desvios dos totais por coluna observados em torno dessa média é zero, mas a soma dos quadrados desses desvios será indicativo das diferenças nos efeitos do tratamento. Portanto, devemos considerar a distribuição amostral da variável aleatória \begin{equation} S=\sum_{j=1}^n \left( R_j-\frac{k(n+1)}{2}\right)^2 \, = \, \sum_{j=1}^n \left(\sum_{i=1}^k \Big( R_{ij}-\frac{n+1}{2}\Big)\right)^2 \end{equation} sob a hipótese nula de não haver diferença entre os \(n\) efeitos do tratamento, isto é, \begin{equation} H_0: \, \theta_1=\theta_2=\cdots=\theta_n\cdot \end{equation} Para este caso nulo, no \(i\)-ésimo bloco os postos são atribuídos completamente aleatórios e cada linha na tabela bidirecional constitui uma permutação aleatória dos primeiros \(n\) inteiros, se não houver empates. Há então um total de \((n!)^k\) conjuntos de entradas distinguíveis na tabela \(k\times n\) e cada um é igualmente provável. Essas possibilidades podem ser enumeradas e o valor de \(S\) calculado para cada um. A função de probabilidade de \(S\) é então \begin{equation} P(S=s) \, = \, \frac{u_s}{(n!)^k}, \end{equation} onde \(u_s\) é o número dessas atribuições que produzem \(s\) como a soma dos quadrados dos desvios totais da coluna.

Os cálculos são consideráveis. Portanto, fora do intervalo de tabelas existentes, uma aproximação para a distribuição nula é geralmente usada para testes de significância. Seja \(\mu=(n+1)/2\), então podemos escrever \begin{equation} \begin{array}{rcl} S & = & \displaystyle \sum_{j=1}^n\sum_{i=1}^k (R_{ij}-\mu)^2 \,+ \, 2\sum_{j=1}^n \sum_{1\leq i < p \leq k} (R_{ij}-\mu)(R_{pj}-\mu) \\ & = & \displaystyle k\sum_{j=1}^n (j-\mu)^2 \, + \, 2U \, = \, \frac{kn(n^2-1)}{12} \, + \, 2U\cdot \end{array} \end{equation}

Os momentos de \(S\) então são determinados pelos momentos de \(U\), que podem ser encontrados usando as seguintes relações \begin{equation} \mbox{E}(R_{ij}) \, = \, \frac{n+1}{2}, \qquad \mbox{Var}(R_{ij}) \, = \, \frac{n^2-1}{12}, \qquad \mbox{Cov}(R_{ij},R_{iq}) \, = \, -\frac{n+1}{2}\cdot \end{equation} Além disso, pelas suposições de modelo, as observações em diferentes linhas são independentes, de modo que, para todo \(i\neq p\), o valor esperado de um produto de funções de \(R_{ij}\) e \(R_{pq}\) é o produto dos valores esperados e \(\mbox{Cov}(R_{ij},R_{pq})=0\). Então \begin{equation} \mbox{E}(U) \, = \, n{k \choose 2} \mbox{Cov}(R_{ij},R_{pj}) \, = \, 0, \end{equation} de maneira que \(\mbox{Var}(U)=\mbox{E}(U^2)\), onde \begin{equation} U^2 \, = \, \displaystyle\sum_{j=1}^n \sum_{1\leq i < p\leq k} (R_{ij}-\mu)^2(R_{pj}-\mu)^2 \, \displaystyle + \, 2\sum_{1\leq j < q\leq k} \sum_{1\leq i < p\leq k} \sum_{1\leq r < s\leq k} (R_{ij}-\mu)(R_{pj}-\mu)(R_{rq}-\mu)(R_{sq}-\mu)\cdot \end{equation} Dado que \(R_{ij}\) e \(R_{pq}\) são independentes sempre que \(i\neq p\), temos \begin{equation} \begin{array}{rcl} \mbox{E}(U^2) & = & \displaystyle\sum_{j=1}^n \sum_{1\leq i < p\leq k}\mbox{Var}(R_{ij})\mbox{Var}(R_{pj}) \, + \, 2 \sum_{1\leq j < q\leq n} {k \choose 2}\mbox{Cov}(R_{ij},R_{iq})\mbox{Cov}(R_{pj},R_{pq}) \\ & = & \displaystyle n{k \choose 2}\frac{(n^2-1)^2}{144} \, + \, \displaystyle 2{n \choose 2}{k \choose 2}\frac{(n+1)^2}{144} \, = \, \displaystyle n^2{k \choose 2}(n+1)^2\frac{(n-1)}{144}\cdot \end{array} \end{equation}

Substituindo estes resultados, temos que \begin{equation} \mbox{E}(S) \, = ,\ \frac{kn(n^2-1)}{12}, \qquad \mbox{Var}(S) \, = \, \frac{n^2k(k-1)(n-1)(n+1)^2}{72}\cdot \end{equation} Uma função linear das variáveis aleatórias, definida como \begin{equation} Q \, = \, \frac{12S}{kn(n+1)} \, = \, \frac{\displaystyle 12\sum_{j=1}^n R_j^2}{kn(n+1)} \, - \, 3k(n+1), \end{equation} tem momentos \(\mbox{E}(Q)=n-1\) e \(\mbox{Var}(Q)=2(n-1)(k-1)/k \approx 2(n-1)\), os quais são os dois primeiros momentos da distribuição qui-quadrado com n-1 graus de liberdade. Os momentos mais altos de \(Q\) também são intimamente aproximados por momentos superiores correspondentes à distribuição qui-quadrado para \(k\) grande. Para todos os efeitos práticos, \(Q\) pode ser tratado como uma variável qui-quadrado com \(n-1\) graus de liberdade.

Exemplo. O conjunto de dados warpbreaks fornece o número de quebras de distorção por tear, em que um tear corresponde a um comprimento fixo de fio.

> wb = aggregate(warpbreaks$breaks, by = list(w = warpbreaks$wool, t = warpbreaks$tension), FUN = mean) > wb w t x 1 A L 44.55556 2 B L 28.22222 3 A M 24.00000 4 B M 28.77778 5 A H 24.55556 6 B H 18.77778 > friedman.test(wb$x, wb$w, wb$t) Friedman rank sum test data: wb$x, wb$w and wb$t Friedman chi-squared = 0.33333, df = 1, p-value = 0.5637

Obtemos por resultado que o número de quebras de distorção \((x)\) é o mesmo segundo o tipo de lã (wool) e a tensão aplicada (tension).

> par(mfrow=c(1,3)) > plot(x ~ w , data = wb, col = "lightgray", ylim = c(18, 45), varwidth = TRUE, subset = t == "L", main = "Tension L") > plot(x ~ w , data = wb, col = "lightgray", ylim = c(18, 45), varwidth = TRUE, subset = t == "M", main = "Tension M") > plot(x ~ w , data = wb, col = "lightgray", ylim = c(18, 45), varwidth = TRUE, subset = t == "H", main = "Tension H") > par(mfrow=c(1,1)) > plot( xtabs(formula = x ~ t + w, data = wb), main = "Comportamento do número de quebras de \ distorção segundo a lã dado a tensão")

> friedman.test(x ~ w | t, data = wb) Friedman rank sum test data: x and w and t Friedman chi-squared = 0.33333, df = 1, p-value = 0.5637

Também verificamos a inexistência de diferenças significativas considerando os diferentes níveis da tensão.

III.3.3 Comparações Múltiplas Não Paramétricas e Intervalos de Confiança Simultâneos

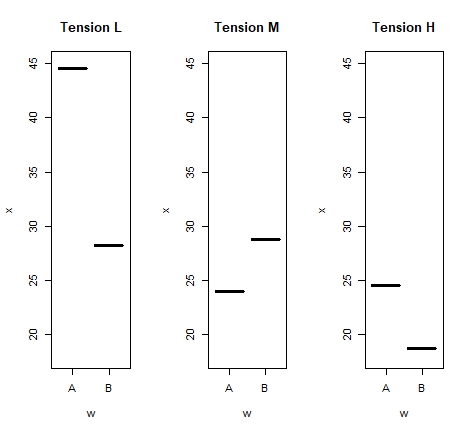As inferências não paramétricas, isto é, sem assumir uma distribuição específica dos dados surgem em uma variedade de problemas como por exemplo na pesquisa biomédica, no caso de dados distorcidos ou dados categóricos ordenados. Embora as inferências paramétricas usualmente lidem com as diferençças entre as médias populacionais, há um foco crescente na medicina sobre medidas de tamanho de efeito em uma base individual. Para duas amostras independentes, digamos, grupo 1 e grupo 2, o efeito relativo mede \begin{equation} p \, = \, P(X \, < \, Y) \, + \, \frac{1}{2}P( X \, = \, Y), \end{equation} que representa a probabilidade de que um sujeito escolhido aleatoriamente no grupo de tratamento 1 revela um valor de resposta \(X\) menor do que um sujeito escolhido aleatoriamente do grupo de tratamento 2 com valor de resposta \(Y\). Se \(p <1/2\), então os valores do grupo 1 tendem a ser maiores que os do grupo 2. Se \(p = 1/2\), nenhuma das observações tende a ser menor ou maior.

O objetivo aqui é apresentar como utilizar o pacote R chamado nparcomp (Konietschke, 2015) que pode ser usado para realizar Comparações Múltiplas Não Paramétricas e Intervalos de Confiança Simultâneos.

Consideramos um modelo ANOVA completamente aleatrizado com \(a\) tratamentos e \(n_i\) replicações independentes dentro de cada tratamento. Sem especificar uma distribuição explícita, por exemplo, distribuição normal, o modelo estatístico pode ser descrito como \begin{equation} X_{ik} \sim F_i, \qquad i=1,2,\cdots,a, \quad k=1,2,\cdots,n_i, \end{equation} onde \(F_i(x) \, = \, P(X_{ik} < x) + \frac{1}{2}P(X_{ik} = x)\) indica a média à esquerda e à direita da versão contínua da função de distribuição. O modelo estatístico não inclui nenhum parâmetro, como as médias, que podem ser usados para descrever os efeitos do tratamento.

Portanto, as funçãoes de distribuição marginal são usadas para descrever efeitos de tratamento como \begin{equation} p_i \, = \, \int H \mbox{d}F_i \, = \, P(Z < X_{i1}) + \frac{1}{2}P(Z \, = \, X_{i1}), \qquad i=1,2,\cdots,a, \end{equation} onde \(H=\frac{1}{a}\sum_{j=1}^a F_j\) denota a distribuição média em sua forma não ponderada. Aqui \(Z\) representa uma variável aleatória com distribuição \(H\) sendo distribuído independentemente de \(X_{i1}\). Estes efeitos são chamados de efeitos relativos não ponderados e podem ser interpretados como a probabilidade de que uma observação \(Z\), escolhida aleatoriamente de todas as observações, tenha um valor menor do que uma observação escolhida aleatoriamente da amostra \(i\). No caso de \(p_i > 1/2\), os dados da amostra tendem a valores maiores que \(Z\). Se \(p_i = 1/2\), nem \(X_{i1}\) nem \(Z\) tendem a valores maiores ou menores. Em particular, se \(p_i < p_j\), então os valores no grupo \(i\) tendem a ser menores que aqueles no grupo \(j\); se \(p_i = p_j\), nenhuma das observações tende a ser menor ou maior.

Procedimento passo a passo para testar as comparações múltiplas do tipo Dunnett (Dunnett, 1955) baseado em postos considera como hipótesis nula \begin{equation} H_0^F \, : \, \left\{ \begin{array}{ccc} F_1 & = & F_2 \\ F_1 & = & F_3 \\ & \vdots & \\ F_1 & = & F_a \end{array} \right., \end{equation} a qual pode ser escrita, equivalentemente, como \begin{equation} H_0^F \, : \, CF \, = \, \begin{pmatrix} -1 & 1 & 0 & \cdots & 0 & 0 \\ -1 & 0 & 1 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ -1 & 0 & 0 \cdots & \cdots & 1 \end{pmatrix} \begin{pmatrix} F_1 \\ F_2 \\ \vdots \\ F_a \end{pmatrix} \, = \, 0, \end{equation} bem como as hipóteses tipo Tukey (Tukey, 1953) de comparações múltiplas \begin{equation} H_0^F \, : \, \left\{ \begin{array}{ccc} F_1 & = & F_2 \\ F_1 & = & F_3 \\ & \vdots & \\ F_1 & = & F_a \\ F_2 & = & F_3 \\ & \vdots & \\ F_{a-1} & = & F_a \end{array} \right., \end{equation} a qual pode ser escrita, equivalentemente, como \begin{equation} H_0^F \, : \, CF \, = \, \begin{pmatrix} -1 & 1 & 0 & \cdots & \cdots & 0 & 0 \\ -1 & 0 & 1 & 0 & \cdots & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ -1 & 0 & 0 & 0 & \cdots & \cdots & 1 \\ 0 & -1 & 1 & 0 & \cdots & 0 & 0 \\ 0 & -1 & 0 & 1 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & \cdots & \cdots & \cdots & -1 & 1 \end{pmatrix} \begin{pmatrix} F_1 \\ F_2 \\ \vdots \\ \vdots \\ F_a \end{pmatrix} \, = \, 0, \end{equation} formulado em termos das funções de distribuição \(F_1,\cdots,F_a\) dos dados. Todos os procedimentos de teste para \(H_0^F\), no entanto, são limitados a problemas de teste e não podem ser usados para construir intervalos de confiança para os efeitos de tratamento subjacentes.

Portanto, Konietschke et al. (2012) propuseram procedimentos de teste de contraste simult&acir;neos e intervalos de confiança múltiplos para os efeitos \(p\). Os procedimentos permitem uma matriz de contraste arbitrária definida pelo usuário \begin{equation} C \, = \, \begin{pmatrix} c_1^\top \\ \vdots \\ c_q^\top \end{pmatrix} \, = \, \begin{pmatrix} c_{11} & \cdots & c_{1a} \\ \vdots & \ddots & \vdots \\ c_{q1} & \cdots & c_{qa} \end{pmatrix}, \end{equation} onde cada vetor de linha \(c_l^\top\) de \(C\) é um contraste, ou seja, cada soma de linha da matriz de contraste é zero por definição.

Por exemplo,comparações múltiplas a um controle são expressas por \begin{equation} H_0^p \, : \, \left\{ \begin{array}{ccc} p_1 & = & p_2 \\ p_1 & = & p_3 \\ & \vdots & \\ p_1 & = & p_a \end{array} \right., \end{equation} a qual pode ser escrita, equivalentemente, como \begin{equation} H_0^p \, : \, Cp \, = \, \begin{pmatrix} -1 & 1 & 0 & \cdots & 0 & 0 \\ -1 & 0 & 1 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ -1 & 0 & 0 \cdots & \cdots & 1 \end{pmatrix} \begin{pmatrix} p_1 \\ p_2 \\ \vdots \\ p_a \end{pmatrix} \, = \, 0 \cdot \end{equation} Todos os pares de comparções são formuladas como \begin{equation} H_0^p \, : \, \left\{ \begin{array}{ccc} p_1 & = & p_2 \\ p_1 & = & p_3 \\ & \vdots & \\ p_1 & = & p_a \\ p_2 & = & p_3 \\ & \vdots & \\ p_{a-1} & = & p_a \end{array} \right., \end{equation} a qual pode ser escrita, equivalentemente, como \begin{equation} H_0^p \, : \, Cp \, = \, \begin{pmatrix} -1 & 1 & 0 & \cdots & \cdots & 0 & 0 \\ -1 & 0 & 1 & 0 & \cdots & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ -1 & 0 & 0 & 0 & \cdots & \cdots & 1 \\ 0 & -1 & 1 & 0 & \cdots & 0 & 0 \\ 0 & -1 & 0 & 1 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & \cdots & \cdots & \cdots & -1 & 1 \end{pmatrix} \begin{pmatrix} p_1 \\ p_2 \\ \vdots \\ \vdots \\ p_a \end{pmatrix} \, = \, 0, \end{equation} as quais, expressas usando a matriz de contraste, assumem a forma \begin{equation} H_0^p \, : \, Cp \, = \, \begin{pmatrix} -1 & 0 & 0 & \cdots & 0 & 1 \\ -1 & 0 & 0 & \cdots & \frac{n_{a-1}}{n_{a-1}+n_a} & \frac{n_a}{n_{a-1}+n_a} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ -1 & \frac{n_2}{n_2+\cdots+n_a} & 0 & \cdots & \cdots & \frac{n_a}{n_2+\cdots+n_a} \end{pmatrix} \begin{pmatrix} p_1 \\ p_2 \\ \vdots \\ p_a \end{pmatrix} \, = \, 0\cdot \end{equation}

Notamos que a hipótese no modelo clássico de Behrens-Fisher está contida nesta configuração geral como um caso especial. Isto é facilmente visto pelo fato de que \(p_i = 1/2\) se \(H\) e \(F_i\) são ambas distribuições simétricas com o mesmo centro de simetria. A hipótese não paramétrica \(H_0^F \, : \, CF = 0\) é muito geral e implica \(H_0^p \, : \, Cp = 0\) e \(H_0^ \, : CF = 0\). A forma das funções de distribuição podem diferir mesmo sob a hipótese nula. No caso especial dos modelos de locação bastante restritivos \(F_i(x) = F(x-\mu_i)\), \(i=1,\cdots,a\), as hipóteses não paramétricas e paramétricas em termos dos parámetros de locação \(\mu_i\) são equivalentes.

Exemplo. No exemplo antrior utilizamos o conjunto de dados warpbreaks. Vejamos agora se existem diferenças entre os níveis de cada fator: tipo de lã (wool) e a tensão aplicada (tension). Primeiro vejamos o comportamento do número de quebras de distorção segundo os dois tipos de lã. Para isso utilizamos o comando npar.t.test no pacote nparcomp de duas formas diferentes.

> a = npar.t.test(x ~ w, data = wb, method = "t.app", alternative = "two.sided", info=FALSE) > summary(a) #-----Nonparametric Test Procedures and Confidence Intervals for relative effects-----# - Alternative Hypothesis: True relative effect p is less or equal than 1/2 - Confidence level: 95 % - Method = Brunner - Munzel - T - Approx with 4 DF #---------------------------Interpretation---------------------------------------------# p(a,b) > 1/2 : b tends to be larger than a #--------------------------------------------------------------------------------------# #----Data Info-------------------------------------------------------------------------# Sample Size A A 3 B B 3 #----Analysis--------------------------------------------------------------------------# Effect Estimator Lower Upper T p.Value 1 p(A,B) 0.444 -0.428 1.317 -0.177 0.868 > par(cex=0.8) > plot(a) > b = npar.t.test(x ~ w, data = wb, method= "permu", alternative = "two.sided", info=FALSE) > summary(b) #-----Nonparametric Test Procedures and Confidence Intervals for relative effects-----# - Alternative Hypothesis: True relative effect p is less or equal than 1/2 - Confidence level: 95 % - Method = Studentized Permutation Test (+ delta-method) #---------------------------Interpretation---------------------------------------------# p(a,b) > 1/2 : b tends to be larger than a #--------------------------------------------------------------------------------------# #----Data Info-------------------------------------------------------------------------# Sample Size A A 3 B B 3 #----Analysis--------------------------------------------------------------------------# Estimator Statistic Lower Upper p.value id 0.444 -0.177 -1.556 2.444 0.99 logit 0.444 -0.175 0.132 0.809 0.99 probit 0.444 -0.176 0.095 0.849 0.99 > plot(b)

Ambos resultados confirmam que não existem diferenças no número de quebras de distorção segundo os dois tipos de lã A e B. Queremos também realizarmos comparações múltiplas com relação aos níveis de tensão, nesta situação utilizamos o comando mctp no mesmo pacote devido a que temos agora três níveis de tensão: L, M, H.

> par(cex=0.8) > a = mctp(x ~ t, data = wb, asy.method = "fisher", type = "Dunnett", alternative = "two.sided", plot.simci = TRUE, info = FALSE) > summary(a) #----------------Nonparametric Multiple Comparisons for relative effects---------------# - Alternative Hypothesis: True differences of relative effects are less or equal than 0 - Estimation Method: Global Pseudo ranks - Type of Contrast : Dunnett - Confidence Level: 95 % - Method = Fisher with 4 DF #--------------------------------------------------------------------------------------# #----Data Info-------------------------------------------------------------------------# Sample Size Effect Lower Upper L L 2 0.75 0.5161836 0.8940190 M M 2 0.50 0.2070143 0.7929857 H H 2 0.25 0.1059810 0.4838164 #----Contrast--------------------------------------------------------------------------# L M H M - L -1 1 0 H - L -1 0 1 #----Analysis--------------------------------------------------------------------------# Estimator Lower Upper Statistic p.Value M - L -0.25 -0.880 0.699 -0.768 0.70814755 H - L -0.50 -0.793 -0.019 -3.496 0.04473533 #----Overall---------------------------------------------------------------------------# Quantile p.Value 1 3.372375 0.04473533 #--------------------------------------------------------------------------------------# > b<-mctp(x ~ t, data = wb, asy.method = "normal", type = "Dunnett", alternative = "two.sided", plot.simci = TRUE, info = FALSE) > summary(b) #----------------Nonparametric Multiple Comparisons for relative effects---------------# - Alternative Hypothesis: True differences of relative effects are less or equal than 0 - Estimation Method: Global Pseudo ranks - Type of Contrast : Dunnett - Confidence Level: 95 % - Method = Normal - Approximation #--------------------------------------------------------------------------------------# #----Data Info-------------------------------------------------------------------------# Sample Size Effect Lower Upper L L 2 0.75 0.5161836 0.8940190 M M 2 0.50 0.2070143 0.7929857 H H 2 0.25 0.1059810 0.4838164 #----Contrast--------------------------------------------------------------------------# L M H M - L -1 1 0 H - L -1 0 1 #----Analysis--------------------------------------------------------------------------# Estimator Lower Upper Statistic p.Value M - L -0.25 -0.946 0.446 -0.802 6.627922e-01 H - L -0.50 -0.763 -0.237 -4.243 4.417502e-05 #----Overall---------------------------------------------------------------------------# Quantile p.Value 1 2.233366 4.417502e-05 #--------------------------------------------------------------------------------------#

III.4 Coeficientes de correlação

O coeficiente de correlação paramémetrico tradicional entre \(X\) e \(Y\) ou coeficiente de correlação de Pearson é a razão entre a covariância do produto entre \(X\) e \(Y\) de seus desvios padrão, ou seja, \begin{equation} \rho \, = \, \frac{\mbox{E}\big( (X-\mu_X)(Y-\mu_Y)\big)}{\sigma_X\sigma_Y}, \end{equation} onde \(\mu_X\), \(\sigma_X\) e \(\mu_Y\), \(\sigma_Y\) são as respectivas médias e desvios-padrão de \(X\) e \(Y\). O parâmetro \(\rho\) requer, é claro, a suposição de variância finita para \(X\) e \(Y\). É uma medida de associação linear entre \(X\) e \(Y\). Pode ser demonstrado que satisfaz as propriedades: \(−1\leq \rho\leq 1\), \(\rho=\pm 1\) se, e somente se, \(Y\) é uma função linear de \(X\) (com probabilidade 1) e \(\rho > ( < ) \, 0\) está associado a um relacionamento linear positivo (negativo) entre \(Y\) e \(X\). Observe que, se \(X\) e \(Y\) forem independentes, então \(\rho = 0\). Em geral, o inverso não é verdadeiro. O contrapositivo, porém, é verdadeiro; isto é, \(\rho \neq 0\) implica que \(X\) e \(Y\) são dependentes.

Normalmente \(\rho\) é estimado por um estimador não paramétrico. O numerador é estimado pela covariância amostral \begin{equation} \frac{1}{n}\sum_{i=1}^n (X_i - \overline{X})(Y_i - \overline{Y}), \end{equation} enquanto que o denominador é estimado pelo produto dos desvios padrão amostrais, com \(n\) e não \(n-1\) como divisores das variâncias amostrais. Isso simplifica que o coeficiente de correlação amostral é dado por \begin{equation} \widehat{\rho} \, = \, \frac{\displaystyle \sum_{i=1}^n (X_i - \overline{X})(Y_i - \overline{Y})} {\displaystyle \sqrt{\sum_{i=1}^n (X_i - \overline{X})^2 \sum_{i=1}^n (Y_i - \overline{Y})^2}}\cdot \end{equation} Similarmente, pode ser mostrado que \(\widehat{\rho}\) satisfaz as propriedades: \(−1\leq \widehat{\rho}\leq 1\), \(\widehat{\rho}=\pm 1\) se existe uma relação linear determinística para a amostra \((X_i, Y_i)\) e \(\widehat{\rho}> (<) \, 0\) associado a uma relação linear positiva (negativa) entre \(Y_i\) e \(X_i\).

O estimador do coeficiente de correlação está diretamente relacionada à regressão simples por mínimos quadrados. Sejam \(\widehat{\sigma}_X\) e \(\widehat{\sigma}_Y\) os respectivos desvios padrão amostrais de \(X\) e \(Y\). Então temos a relação \begin{equation} \widehat{\rho} \, = \, \frac{\widehat{\sigma}_X}{\widehat{\sigma}_Y}\widehat{\beta}, \end{equation} onde \(\widehat{\beta}\) é o estimador de mínimos quadrados da inclinação na regressão simples de \(Y_i\) em \(X_i\). Pode-se demonstrar que, sob a hipótese nula, \(\sqrt{n}\widehat{\beta}\) é assintoticamente \(N(0,1)\). A inferência para \(\widehat{\rho}\) pode ser baseada neste resultado assintótico, mas geralmente a aproximação \(t-Student\) á usada.

Se fizermos a suposição mais forte de que o vetor aleatório \((X,Y)\) tem distribuição normal bivariada, então \(\widehat{\rho}\) é o estimador de máxima verossimilhança de \(\rho\). Com base na sua expressão, sob \(H_0: \, \rho=0\), a estatística \begin{equation} t_{obs} \, = \, \frac{\sqrt{n-2}\widehat{\rho}}{\sqrt{1-\widehat{\rho}^2}}, \end{equation} tem distribuição \(t-Student\) com \(n-2\) graus de liberdade. Assim, um teste com nível de signicância \(\alpha\) rejeita a hipótese \(H_0\) em favor de \(H_A: \rho\neq 0\) se \(|t_{obs}|> t_{\alpha/2, n-2}\). Além disso, para \(\rho\) geral, pode ser mostrado que \begin{equation} log\left(\frac{1+\widehat{\rho}}{1-\widehat{\rho}}\right) \end{equation} é aproximadamente normal com esperança \((1+\rho)(1-\rho)\). Com base nisso, intervalos de confiança aproximados para \(\rho\) podem ser construídos. Na prática, geralmente a forte suposição de normalidade bivariada não pode ser feita. Nesse caso, o teste \(t\) e o intervalo de confiança são aproximados. Para cálculo no R consideramos \(X\) e \(Y\) vetores e utilizamos a função cor.test.

III.4.1 Coeficiente de correlação de Kendall

Proposto por Maurice G. Kendall e Bernard Babington Smith em 1939 (Kendall, M.G. & Smith, B.B., 1939), o coeficiente de concordância de Kendall é uma medida da concordância entre várias variáveis quantitativas ou semiquantitativas que estão avaliando um conjunto de \(n\) objetos de interesse. Nas ciências sociais, as variáveis são frequentemente pessoas, avaliando assuntos ou situações diferentes. Na ecologia podem ser espécies cujas abundâncias são usadas para avaliar a qualidade do habitat nos locais de estudo. Na taxonomia, podem ser características medidas sobre diferentes espécies dentre outras situações de interesse.

O coeficiente de correlação de Kendall \(\tau_K\) será a primeira medida não paramétrica de associação que discutimos. Como acima, seja \((X,Y)\) um vetor aleatório contínuo. O coeficiente \(\tau_K\) de Kendall é uma medida de monotonicidade entre \(X\) e \(Y\). Consideremos dois pares de vetores aleatórios \((X_1,Y_1)\) e \((X_2,Y_2)\) independentes com a mesma distribuição de \((X,Y)\). Dizemos que os pares \((X_1,Y_1)\) e \((X_2,Y_2)\) são concordantes ou discordantes se \begin{equation} \mbox{sign}\big((X_1-X_2)(Y_1-Y_2)\big) \, = \, 1 \qquad \mbox{ou} \qquad \mbox{sign}\big((X_1-X_2)(Y_1-Y_2)\big) \, = \, -1, \end{equation} respectivamente. Pares concordantes são indicativos de monotonicidade crescente entre \(X\) e \(Y\), enquanto pares discordantes indicam monotonicidade decrescente. O \(\tau_K\) de Kendall mede essa monotonicidade em um sentido de probabilidade. É definido por \begin{equation} \tau_K \, = \, P\Big(\mbox{sign}\big((X_1-X_2)(Y_1-Y_2)\big) \, = \, 1 \Big) \, - \, P\Big(\mbox{sign}\big((X_1-X_2)(Y_1-Y_2)\big) \, = \, -1 \Big) \cdot \end{equation}

Pode ser mostrado que \(−1\leq \tau_K \leq 1\); \(\tau_K> 0\) indica monotonicidade crescente, \(\tau_K< 0\) indica monotonicidade decrescente e \(\tau_K = 0\) não reflete monotonicidade. Segue-se que, se \(X\) e \(Y\) são independentes, então \(\tau_k=0\). Enquanto o inverso não é verdadeiro, o contrapositivo é verdadeiro; isto é, \(\tau_K \neq 0\) implica que \(X\) e \(Y\) são dependentes.

Usando a amostra aleatória \((X_1,Y_1), (X_2,Y_2),\cdots ,(X_n,Y_n)\), um estimador direto de \(\tau_K\) é simplesmente contar o número de pares concordantes na amostra e subtrair aquele número de pares discordantes. A padronização dessa estatística leva a \begin{equation} \widehat{\tau}_K \, = \, \frac{1}{\displaystyle {n \choose 2}}\sum_{i< j} \mbox{sign}\big((X_i-X_j)(Y_i-Y_j)\big), \end{equation} como nosso estimador de \(\tau_K\). Como a estatística \(\widehat{\tau}_K\) é um coeficiente \(\tau_K\) de Kendall baseado na distribuição amostral empírica, compartilha as mesmas propriedades; isto é, \(\widehat{\tau}_K\) está entre -1 e 1 e valores positivos de \(\widehat{\tau}_K\) refletem monotonicidade crescente enquanto valores negativos refletem monotonicidade decrescente. Pode ser mostrado que \(\widehat{\tau}_K\) é um estimador não viciado e \(\tau_K\). Além disso, sob a suposição de que \(X\) e \(Y\) serem independentes, a distribuição do estimador \(\widehat{\tau}_K\) é livre de parâmetros com esperança 0 e variância \(2(2n+5)/\big(9n(n-1)\big)\). Testes de hipóteses podem ser baseados na distribuição exata em amostras finitas. No R o cálculo deste estimador é obtido pela função cor.test com method = "kendall".

III.4.2 Coeficiente de correlação de Spearman

Na definição do coeficiente de correlação de Spearman \(\rho_S\) (Spearman, C.E., 1904), é mais fácil começar com seu estimador. Considere a amostra aleatória \((X_1,Y_1),(X_2,Y_2),\cdots,(X_n,Y_n)\). Denotemos por \(R(X_i)\) o posto de \(X_i\) entre \(X_1,X_2,\cdots,X_n\) e da mesma forma denotemos \(R(Y_i)\) como o posto de \(Y_i\) entre \(Y_1,Y_2,\cdots,Y_n\). A estimativa de \(\rho_S\) é simplesmente o coeficiente de correlação da amostra com \(X_i\) e \(Y_i\) substituídos respectivamente por \(R(X_i)\) e \(R(Y_i)\). Seja então \(\widehat{\rho}_S\) denotar esse coeficiente de correlação. Note que o denominador de \(\widehat{\rho}_S\) é uma constante e que a média amostral das classificações é \((n+1)/2\). Simplificação leva à fórmula \begin{equation} \widehat{\rho}_S \, = \, \frac{\displaystyle \sum_{i=1}^n \Big( R(X_i)-\frac{n+1}{2}\Big)\Big(R(Y_i)-\frac{n+1}{2}\Big)} {\displaystyle \frac{n(n^2-1)}{12}} \end{equation}

Esta estatística é um coeficiente de correlação, portanto, assume valores entre \(\pm 1\) e é \(\pm 1\) se houver uma relação estritamente crescente ou decrescente entre \(X_i\) e \(Y_i\). Portanto, similar ao coeficiente de Kendall \(\tau_K\), ele estima a monotonicidade entre as amostras. Pode ser mostrado que \begin{equation} \mbox{E}(\widehat{\rho}_S) \, = \, \frac{3}{n+1}\Big( \tau_K+\frac{n-2}{2\gamma -1}\Big), \end{equation} onde \(\gamma=P\big((X_2-X_1)(Y_3-Y_1)>0\big)\). O estimador de \(\rho_S\) não é tão fácil de interpretar quanto o do \(\tau_K\).

Se \(X\) e \(Y\) forem independentes, segue-se que \(\widehat{\rho}_S\) é um estatística com distribuição livre de parâmetros, isto devido a que a média é 0 e a variância \(1/(n−1)\). Aceitamos \(H_A: \, X \; \mbox{e} \; Y \; \mbox{são dependentes}\) para grandes valores de \(|\widehat{\rho}_S|\). Este teste pode ser realizado usando a distribuição exata ou aproximada usando a estatística \(z=\sqrt{n-1}\widehat{\rho}_S\). Em aplicações, no entanto, a aproximação \(t-Student\) é frequentemente utilizada, onde \begin{equation} t_{obs} \, = \, \frac{\sqrt{n-2}\widehat{\rho}_S}{\sqrt{1-\widehat{\rho}_S^2}}\cdot \end{equation}

No R o cálculo deste estimador é obtido pela função cor.test com method = "spearman". Isso calcula a estatística de teste e o \(p-valor\), mas não um intervalo de confiança para \(\rho_S\). Embora o parâmetro \(\rho_S\) seja difícil de interpretar, no entanto, os intervalos de confiança são importantes porque dão uma noção da força ou tamanho do efeito da estimativa.

III.5 Exercícios

1. Pesquisadores investigaram a mudança em acidentes fatais com veículos automotores depois que a idade mínima legal para beber foi aumentada em 10 estados. Seus dados foram as proporções do número de fatalidades noturnas com um único veículo com o número de motoristas licenciados na faixa etária afetada antes e depois de as leis serem alteradas para aumentar a idade de consumo de álcool. Os pesquisadores levantaram a hipótese de que a idade mínima para beber resultou em uma redução do índice médio de mortalidade. Investigue essa hipótese.

   Estado		Florida		Georgia		Ilinois		Oiwa		Maine		Michigan		Montana		Nebraska		New Hampshire		Tennesse
   Idades afetadas		18		18		19-20		18		18-19		18-20		18		19		18-19		18
   Proporção antes		0.262		0.295		0.216		0.287		0.277		0.223		0.512		0.237		0.348		0.342
   Proporção depois		0.202		0.227		0.191		0.209		0.299		0.151		0.471		0.151		0.336		0.307



2. A conclusão no problema acima foi que a diferença mediana (Antes - Depois) foi positiva para a faixa etária afetada, mas isso não implica que a redução foi o resultado de leis que elevaram a idade mínima legal para beber. Outros fatores, contramedidas ou campanhas publicitárias pode ter afetado as razães de fatalidade. A fim de investigar mais, esses pesquisadores compararam a proporções Antes - Após para a faixa etária afetada com as razões de diferença correspondentes para a faixa etária de 25 a 29 anos, que não foram afetadas pela mudança na lei, conforme mostrado na Tabela a seguir. Realize um teste apropriado e escreva um relatório com suas conclusões.

   Estado		Florida		Georgia		Ilinois		Oiwa		Maine		Michigan		Montana		Nebraska		New Hampshire		Tennesse
   Faixa etária afetada		0.060		0.068		0.025		0.078		-0.022		0.072		0.041		0.086		0.012		0.035
   Faixa etária 25 - 29		-0.025		-0.023		0.004		-0.008		0.061		0.015		-0.035		-0.016		-0.061		-0.051



3. Um determinado estudo foi destinado a investigar se a ansiedade ao computador muda entre o início e o fim de um curso sobre introdução aos computadores. Os alunos foram submetidos a um teste para medir a ansiedade ao computador no início do período e, novamente, no final do curso de verão de 5 semanas. Pontuações altas neste teste indicam um alto nível de ansiedade. Para os dados na tabela sobre 14 alunos, determine se a ansiedade ao computador foi reduzida ao longo do período.

   Aluno		A		B		C		D		E		F		G		H		I		J		K		L		M		N
   Antes		20		21		23		26		32		27		38		34		28		20		29		22		30		25
   Após		20		18		10		16		11		20		20		19		13		21		12		15		14		17



4. Vinte e quatro alunos fizeram o exame intercalar e o final em um curso de redação. As notas numéricas não foram dadas na final, mas cada aluno foi classificado como sem alteração, melhoria ou redução do nível de desempenho em comparação com a nota no meio do período. Seis apresentaram melhora, 5 não apresentaram alteração e 13 tiveram nível reduzido de desempenho. Encontre o \(p-valor\) para um teste apropriado.


5. Reduzir a pressão alta pela dieta requer redução da ingestão de sódio, o que geralmente requer a mudança de alimentos processados para suas contrapartes naturais. Abaixo estão listados os teores médios de sódio de cinco alimentos comuns em forma processada e natural para quantidades equivalentes. Encontre uma estimativa do intervalo de confiança da diferença mediana (processada menos natural) com um coeficiente de confiança de pelo menos 0.87 usando dois procedimentos diferentes.

   Alimentos naturais				Alimentos processados
   MIlho de espiga		2		Milho em conserva		251
   Frango		63		Frango frito		1220
   Lombo à terra		60		Salsicha de carne bovina		461
   Feijão		3		Feijão enlatado		300
   Atum fresco		40		Atum enlatado		409



6. Em um teste de dois tipos de pluviômetro, 69 do tipo A e 12 do tipo B foram distribuídos aleatoriamente em uma pequena área. Em um determinado período ocorreram 14 tempestades e as quantidades médias de chuva registradas para cada tempestade pelos dois tipos de manômetro são as seguintes:

   Tempestade		Tipo A		Tipo B			Tempestade		Tipo A		Tipo B
   1		1.38		1.42			8		2.63		2.69
   2		9.69		10.37			9		2.44		2.68
   3		0.39		0.39			10		0.56		0.53
   4		1.42		1.46			11		0.69		0.72
   5		0.54		0.55			12		0.71		0.72
   6		5.94		6.15			13		0.95		0.90
   7		0.59		0.61			14		0.55		0.52

   Outro usuário afirma ter descoberto que o medidor tipo B fornece leituras médias consistentemente mais altas do que o tipo A. Esses resultados confirmam tal conclusão? Investigue usando dois procedimentos de teste não paramétricos diferentes, encontrando o \(p-valor\) de
   • (a) Distribuição exata.
   • (b) Aproximação à distribuição exata em grandes amostras.


7. Um fabricante de protetor solar está testando uma nova fórmula para ver se ela oferece mais proteção contra queimaduras solares do que a fórmula antiga. O fabricante escolheu 10 pessoas aleatoriamente entre os funcionários da empresa, aplicou os dois tipos de loção nas costas, um tipo de cada lado e expôs suas costas a uma quantidade controlada mas intensa de sol. O grau da queimadura solar foi medido para cada lado de cada sujeito, com os resultados mostrados abaixo sendo que os números mais altos representam queimaduras solares mais graves.

   Sujeito		1		2		3		4		5		6		7		8		9		10
   Fórmula antiga		41		42		48		38		38		45		21		28		29		14
   Fórmula nova		37		39		31		39		34		47		19		30		25		8

   • (a) Testar a hipótese nula de que a diferença (antiga - nova) do grau de queimadura solar tem mediana zero contra a alternativa unilateral que é negativa, assumindo que as diferenças são simétricas. A nova fórmula parece ser eficaz?
   • (b) Encontre um intervalo de confiança para a diferença mediana, assumindo simetria e com coeficiente de confiança próximo de 0.90.
   • (c) Faça (a) e (b) sem assumir simetria.


8. Em um teste de pesquisa de mercado, 15 homens adultos foram solicitados a raspar um lado do rosto com uma lâmina de barbear da marca A e o outro lado com uma lâmina de barbear da marca B e indicar sua lâmina preferida. Doze homens preferiram a marca A. Encontre o \(p-valor\) para a alternativa de que a probabilidade de preferir a marca A é maior que 0.5.


9. A fim de testar a eficácia de um programa de treinamento de vendas proposto por uma empresa de especialistas em treinamento, uma empresa de mobiliário doméstico seleciona seis representantes de vendas ao acaso para fazer o curso. Os dados abaixo são vendas brutas desses representantes antes e depois do curso.

   Representante		1		2		3		4		5		6
   Vendas antes		90		83		105		97		110		78
   Vendas após		97		80		110		93		123		84

   • (a) Indique as hipóteses nula e alternativa e use o teste do sinal para encontrar um \(p-valor\) relevante para a questão de saber se o curso é eficaz.
   • (b) Use o procedimento de teste de sinais no nível mais próximo de 0.90 para encontrar um estimativa do intervalo da diferença mediana de vendas (antes - antes). Dê o nível exato.


10. Um estudo de 5 anos atrás relatou que a mediana da quantidade de sono por adultos americanos é de 7.5 horas de 24 com um desvio padrão de 1.5 horas e que 5% da população dormem 6 ou menos horas enquanto outros 5% dormem 9 ou mais horas. Uma amostra atual de oito adultos relatou suas quantidades médias de sono por 24 horas como 7.2, 8.3, 5.6, 7.4, 7.8, 5.2, 9.1 e 5.8 horas. Use os procedimentos estatísticos mais apropriados para determinar se os adultos americanos dormem menos hoje do que há cinco anos e justifique sua escolha. Você deve pelo menos testar a hipóteses sobre os quantis de ordem 0.05, 0.50 e 0.95.


11. Se \(X_{(1)}\) e \(X_{(n)}\) são as estatísticas de ordem menor e maior, respectivamente, em uma amostra de tamanho \(n\) de uma população qualquer com função de distribuição contínua \(F_X\) de mediana \(\kappa_{0.50}\), encontre o menor valor de \(n\) tal que:
    • (a) \(P\big( X_{(1)} < \kappa_{0.50} < X_{(n)} \big)\geq 0.99\).
    • (b) \( P\big( F_X(X_{(n)}) - F_X(X_{(1)}) \geq 0.50 \big)\geq 0.95\).


12. Um psicólogo observa o tempo total (em segundos) necessário para realizar uma série de tarefas manuais simples para cada uma das oito crianças com dificuldades de aprendizagem e sete crianças sem dificuldades de aprendizagem. Os tempos são:

    Sem dificuldades	204	218	197	183	227	233	191
    Com dificuldades	243	228	261	202	343	242	220	239

    Use um teste adequado para descobrir se o psicólogo tem justificativa para afirmar que essas amostras provavelmente são de populações diferentes.


13. Uma grande empresa ficou perturbada com o número de horas perdidas por mês devido a acidentes em fábricas e instituiu um extenso programa de segurança industrial. Os dados abaixo mostram o número de pessoas-horas perdidas em um mês em cada uma das oito plantas diferentes antes e depois que o programa de segurança foi estabelecido. O programa de segurança foi eficaz na redução do tempo perdido por acidentes? Suponha que a distribuição das diferenças seja simétrica.

    Planta	1	2	3	4	5	6	7	8
    Antes	51.2	46.5	24.1	10.2	65.3	92.1	30.3	49.2
    Depois	45.8	41.3	15.8	11.1	58.5	70.3	31.6	35.4



14. Fogões Hotpot usam um isolamento de forno padrão. Para testar sua eficácia, foram coletadas amostras aleatórias da linha de produção e aqueceram-se os fornos selecionados a 400°C, observando-se o tempo necessário para esfriar a 350°C após o desligamento. Para uma amostra de 8 fornos, os tempos em minutos foram: \begin{equation} 15.7 \quad 14.8 \quad 14.2 \quad 16.1 \quad 15.3 \quad 13.9 \quad 17.2 \quad 14.9 \end{equation} Decide-se depois explorar um isolamento mais barato e usando isso em uma amostra de 9, os tempos tomados para a mesma queda de temperatura foram: \begin{equation} 13.7 \quad 14.1 \quad 14.7 \quad 15.4 \quad 15.6 \quad 14.4 \quad 12.9 \quad 15.1 \quad 14.0 \end{equation} A empresa está justificada em afirmar que não há evidência real de uma taxa diferente de perda de calor? Obtenha um limite de confiança de 95& para a diferença na perda de calor mediana.


15. Os dados baixo correspondem às larguras da primeira articulação do segundo tarso para duas espécies do inseto Chaetocnema. Estas indicam diferenças populacionais entre as distribuições de largura para as duas espécies?

    Espécie A	131	134	137	127	128	118	134	129	131	115
    Espécie B	107	122	144	131	108	118	122	127	125	124



16. Pesquisadores fornecem dados da variação percentual do açúcar no sangue durante período de 1 hora para coelhos que receberam dois diferentes doses de um medicamento. Há evidência de uma diferença de resposta entre os níveis?

    Dosage I	0.21	-16.20	-10.10	-8.67	-11.13	1.96	-10.19	-15.87	-12.81
    Dosage II	1.59	2.66	-6.27	-2.32	-10.87	7.23	-3.76	3.02	15.01



17. As estatísticas do censo de 2000 para o estado de Alabama dão as variações percentuais na população entre 1990 e 2000 para cada um dos 67 municípios. Esses municípios foram divididos em dois grupos mutuamente independentes, rurais e urbanos, de acordo com o tamanho da população de menos de 25.000 em 2000 ou não. Amostras aleatórias de nove municípios rurais e sete urbanos deram os seguintes dados sobre a variação percentual da população:

    Rural	1.1	-21.7	-16.3	-11.3	-10.4	-7.0	-2.0	1.9	6.2
    Urbano	-2.4	9.9	14.2	18.4	20.1	23.1	70.4

    Utilize todos os métodos estudos para verificar a hipótese nula de igualdade de distribuições.


18. Uma amostra de três meninas e cinco meninos recebem instruções sobre como completar uma determinada tarefa. Em seguida, eles são convidados a executar a tarefa mais e mais vezes até que completá-lo corretamente. O número de repetições necessárias para o preenchimento correto é 1, 2 e 5 para as meninas e 4, 8, 9, 10 e 12 para os meninos. Encontre o \(p\)-valor para a alternativa que, em média, as meninas aprendem a tarefa mais rapidamente que os meninos e encontre uma estimativa do intervalo de confiança para a diferença \(\theta=M_y - M_X\) com um coeficiente de confiança pelo menos igual a 0.85, usando o teste da mediana.


19. Um pesquisador está interessado em saber se um novo medicamento é melhor que um placebo no tratamento de uma determinada doença. Devido à natureza da doença, apenas um número limitado de pacientes pode ser encontrado. Destes, 5 são aleatoriamente designados para o placebo e 5 para o novo medicamento. Suponha que a concentração de uma determinada substância química no sangue seja medida e que a medição menor seja melhor. Os dados são os seguintes: \begin{equation} \begin{array}{cc} \mbox{Droga:} \quad 3.2, 2.1, 2.3, 1.2, 1.5 & \mbox{Placebo:} \quad 3.4, 3.5, 4.1, 1.7, 2.1 \end{array} \end{equation}
    • (a) Use o teste da mediana para verificar a hipótese. Quais suposições estamos fazendo?
    • (b) Use o teste da mediana para calcular um intervalo de confiança para a diferença entre as medianas. Qual é o maior nível de confiança possível? Quais suposições estamos fazendo para este procedimento?


20. Uma tarefa de correspondência para amostra (MTS) é usada por psicólogos para entender como outras espécies percebem e usam relações de identidade. Uma tarefa padrão do MTS consiste em fazer com que os sujeitos observem um estímulo amostral e, em seguida, desloquem o sujeito se ele responder a um estímulo amostral idêntico. Em seguida, o psicólogo estuda a capacidade dos sujeitos de transferir o conceito de correspondência para outros estímulos amostrais. Oden, Thompson & Premack (1988) relataram um estudo no qual quatro chimpanzés infantis aprenderam uma tarefa de MTS com apenas dois estímulos amostrais de treinamento. Em seguida, os chimpanzés foram testados em sua capacidade de transferir o aprendizado para três tipos de novos itens, classificados como Objetos, Tecidos e Alimentos. Os dados foram registrados como número de correspondências corretas em um total de 24 tentativas. Um dos objetivos do estudo foi mostrar que o conceito de correspondência é amplamente interpretado pelos chimpanzés, independentemente do tipo de estímulo amostral. Determine se os dados na Tabela suportam essa teoria.

    Chimpanzé		Treinamento		Objeto		Tecido		Alimento
    Whiskey		20		22		22		18
    Liza		23		19		22		13
    Opal		18		20		18		15
    Frieda		1		21		19		19



21. Muitos psicólogos desenvolveram teorias sobre como diferentes tipos de dominância cerebral podem afetar a capacidade de recordar informações apresentadas em vários formatos. Brown & Evans (1986) compararam a capacidade de recordar de indivíduos classificados em três grupos de acordo com a sua abordagem de resolução de problemas, como resultado de suas pontuações na Pesquisa do Processo de Informação Humana. Os grupos de árvores são Esquerda (ativa, verbal, lógica), Direita (receptiva, espacial, intuitiva) e Integrativa (combinação de direita e esquerda). Informações foram apresentadas aos sujeitos em forma de tabela sobre o número de médicos que praticam em seis estados diferentes. A recordação foi medida pela precisão com que os sujeitos conseguiram classificar os estados do maior para o menor após a conclusão da apresentação. Para as pontuações na Tabela, determine se a capacidade de recordação mediana é a mesma para os três grupos (pontuações mais altas indicam maior recordação).

    Direita		Esquerda		Integrativa
    35		17		28
    32		20		30
    38		25		31
    29		15		25
    36		10		26
    31		12		24
    33		8		24
    35		16		27

    
    
22. Andrews (1989) examina atitudes em relação à publicidade de alunos de graduação em marketing em universidades de seis diferentes regiões geográficas. As atitudes foram medidas por respostas a um questionário que reduzam as respostas em uma escala Likert de 7 pontos (1 = discordo totalmente e 7 = concordo totalmente). Três afirmações sobre o questionário relacionadas à dimensão social foram: (1) a maioria das propagandas insulta a inteligência do consumidor médio; (2) publicidade muitas vezes convence as pessoas a comprar coisas que não deveriam comprar; e (3) em geral, as propagandas apresentam uma imagem real do produto que está sendo anunciado. Para a pontuação média dada na Tabela, determine se existem diferenças regionais de atitude para a dimensão social.

    Região		Insulta		Convence		Verdadeira
    Noroeste		3.69		4.48		3.69
    Centro oeste		4.22		3.75		3.25
    Nordeste		3.63		4.54		4.09
    Sudoeste		4.16		4.35		3.61
    Central sul		3.96		4.73		3.41
    Sudeste		3.78		4.49		3.64



23. Uma amostra aleatórias de 100 executivos de companhias de seguros, 100 executivos de empresas de transporte e 100 executivos de empresas de mídia foram classificadas de acordo com o mais alto nível de estudo usando o código 10 = alguma faculdade, 20 = bacharel, 30 = mestrado, 40 = mais do que o mestrado. Os resultados são mostrados abaixo. Determine se o nível de escolaridade mediano é o mesmo para os três grupos.

    Estudo		Seguro		Transporte		Mídia
    10		19		31		33
    20		20		37		34
    30		36		20		21
    40		25		12		12

    
    
24. Quatro diferentes métodos experimentais de tratamento da esquizofrenia - (1) tratamentos de choque semanais, (2) tratamentos semanais de inalações de dióxido de carbono, (3) tratamento de choque quinzenal alternado com inalações bissemanais de dióxido de carbono e (4) tratamento medicamentoso tranqüilizante - são comparados num grupo de pacientes esquizofrênicos aleatoriamente em quatro grupos de tratamento. Os dados abaixo são o número de pacientes que melhoraram e não melhoraram em quatro semanas de tratamento. Teste a hipótese nula de que os tratamentos são igualmente eficazes.

    Tratamento		Melhoraram		Não melhoraram
    1		43		12
    2		24		28
    3		32		16
    4		29		24



25. Uma empresa está testando quatro cereais para determinar as preferências de gosto dos compradores em potencial. Quatro painéis diferentes de pessoas são selecionados independentemente: um cereal é apresentado a todos os membros de cada painel. Após o teste, pergunta-se a cada pessoa se ele compraria o produto. O resultado é mostrado abaixo. Teste a hipótese de que a preferência de gosto é a mesma para cada cereal.

    		Cereal
    		A		B		C		D
    Número que comprariam		75		80		57		80
    Número que não comprariam		50		60		43		70



26. Abaixo estão quatro conjuntos de cinco medições, cada conjunto de uma matriz de dados da suavidade de um determinado tipo de papel, cada conjunto obtido a partir de um laboratório diferente. Teste se a suavidade mediana pode ser igual à mesma para todos os laboratórios.

    Laboratório		Dado
    A		38.7		41.5		43.8		44.5		45.5
    B		39.2		39.3		39.7		41.4		41.8
    C		34.0		35.0		39.0		40.0		43.0
    D		34.1		34.8		34.9		35.4		37.2



27. Sete alunos participaram de dois exames: matemática e inglês. Suas notas foram \begin{equation} (5.6, 4.3), \, (8.5, 6.4), \, (5.3, 3.4), \, (4.5, 9.0), \, (7.1, 6.8),\, (2.4, 5.1), \, (6.0, 5.5) \cdot \end{equation} Teste se as notas para os dois assuntos estão correlacionadas ou não, usando as estatísticas de Spearman e Kendall.


28. Um concurso de beleza tem oito concorrentes. Os dois juízes são convidados a classificar as competidoras em uma ordem preferencial de pulcritude. Os resultados são mostrados na tabela abaixo. Responda as partes (a) e (b) usando (i) o procedimento do coeficiente \(\tau_K\) de Kendall e (ii) o procedimento do coeficiente de correlação de Spearman:

    	Concorrente
    Juiz	A	B	C	D	E	F	G	H
    1	2	1	3	5	4	8	7	6
    2	1	2	4	5	7	6	8	3

    • (a) Calcule a medida de associação.
    • (b) Testar a hipótese nula de que os juízes classificaram os competidores de forma independente.
    • (c) Encontre uma estimativa para o intervalo de confiança de 95% de \(\tau_K\).


29. Um cientista político queria examinar a relação da imagem eleitoral de um candidato político conservador e a distância em milhas entre a residência do eleitor e a residência do candidato. Cada um dos 12 eleitores classificou o candidato em uma escala de 1 a 20. Os resultados são mostrados na tabela a seguir.

    Eleitor	Avaliação	Distância
    1	12	75
    2	7	165
    3	5	300
    4	19	15
    5	17	180
    6	12	240
    7	9	120
    8	18	60
    9	3	230
    10	8	200
    11	15	130
    12	4	130

    Esses dados fornecem evidências suficientes para indicar uma correlação negativa entre a classificação e a distância?


30. Dois gourmets, A e B, classificaram 20 refeições em uma escala de 1 a 10. Os dados são mostrados na tabela que acompanha. Os dados fornecem evidências suficientes para indicar que um dos gourmets tende a dar classificações mais altas do que o outro?

    Refeição	A	B		Refeição	A	B
    1	6	8		11	6	9
    2	4	5		12	8	5
    3	7	4		13	4	2
    4	8	7		14	3	3
    5	2	3		15	6	8
    6	7	4		16	9	10
    7	9	9		17	9	8
    8	7	8		18	4	6
    9	2	5		19	4	3
    10	4	3		20	5	5



31. O Census Bureau ou o United States Census Bureau faz parte do Departamento de Comércio dos Estados Unidos. É a agência governamental encarregada pelo censo nos Estados Unidos. O Census Bureau informou que os hispânicos devem ultrapassar os negros como a maior minoria nos Estados Unidos até o ano de 2030. Use dois testes diferentes para ver se existe uma relação direta entre o número de hispânicos e a porcentagem da população do estado nos nove estados abaixo.

    Estado	Hispânicos (em milhões)	% população do estado
    California	6.6	23
    Texas	4.1	24
    New York	2.1	12
    Florida	1.5	12
    Ilinois	0.8	7
    Arizona	0.6	18
    New Jersey	0.6	8
    New Mexico	0.5	35
    Colorado	0.4	11



32. Despesas em pesquisa e desenvolvimento (P&D) financiadas por empresas são atualmente cerca de 2.7% das vendas no Japão e 2.8% das vendas nos Estados Unidos. No entanto, quando esses números são analisados separadamente de acordo com a indústria, os seguintes dados mostram algumas grandes diferenças.

    Indústria	Japão	Estados Unidos
    Alimentos	0.8	0.4
    Têxteis	1.2	0.5
    Papel	0.7	1.3
    Produtos Químicos	3.8	4.7
    Petróleo	0.4	0.7
    Borracha	2.9	2.2
    Metais ferrosos	1.9	0.5
    Metais não ferrosos	1.9	1.4
    Produtos metálicos	1.6	1.3
    Maquinaria	2.7	5.8
    Equipamento eléctrico	5.1	4.8
    Veículos a motor	3.0	3.2
    Outros equipamentos de transporte	2.6	1.2
    Instrumentos	4.5	9.0

    • (a) Use o teste de classificação assinada para determinar se o Japão gasta uma porcentagem maior do que os Estados Unidos em pesquisa e desenvolvimento.
    • (b) Determinar se existe uma relação positiva significativa entre as percentagens gastas pelo Japão e pelos Estados Unidos, utilize dois métodos diferentes.