Distribuição geométrica truncada
Elias T. Krainski
Maio 30, 2017
Problema
Um jogador lança uma moeda equilibrada até a ocorrência de dois resultados iguais sucessivos. Determine o valor esperado do número de lançamentos.
Solução
Seja a probabilidade de eventos sucessivos iguais em experimentos de \(Bernoulli(p)\).
\[\begin{array}{rcl} P(X_i=X_{i-1}) & = & P(\{X_i=0 \cap X_{i-1}=0\} \cup \{X_i=1 \cap X_{i-1}=1\}) \\ & = & P(\{X_i=0 \cap X_{i-1}=0\}) + P(\{X_i=1 \cap X_{i-1}=1\}) \rightarrow \textrm{Mutuamente exclusivos}\\ & = & P(X_i=0)P(X_{i-1}=0) + P(X_i=1)P(X_{i-1}=1) \rightarrow \textrm{Independentes}\\ & = & p^2 + (1-p)^2 = s \end{array} \]
Assim, a probabilidade de eventos sucessivos iguais é \[s = p^2 + (1-p)^2\] e vamos definir como sucesso: resultado num lançamento ser igual ao resultado no lançamento anterior. Como o experimento consiste em lançamentos até este sucesso, podemos considerar a distribuição geométrica, porém, considerando que \[P(Y=k) = s(1-s)^{k-2}, \; k=2,3,...\]
Verificamos que \[ \sum_{k=2}^\infty P(Y=k) = \sum_{k=2}^\infty s(1-s)^{k-2} = \sum_{k=0}^\infty s(1-s)^{k} = s\sum_{k=0}^\infty (1-s)^{k} = s\frac{1}{s}=1 \]
Experança
\[\begin{array}{rcl} E(Y) & = &\sum_{k=2}^\infty k P(Y=k) = \sum_{k=2}^\infty k s(1-s)^{k-2} \\ & = & s\sum_{k=2}^\infty k \frac{(1-s)^{k-1}}{1-s} \\ & = & \frac{s}{1-s}\sum_{k=2}^\infty k(1-s)^{k-1} \\ & = & -\frac{s}{1-s}\sum_{k=2}^\infty \frac{\partial}{\partial s} (1-s)^{k} \\ & = & -\frac{s}{1-s}\frac{\partial}{\partial s} \sum_{k=2}^\infty (1-s)^{k} \rightarrow \textrm{Ordem pode ser trocada se a soma existe} \\ & = & -\frac{s}{1-s}\frac{\partial}{\partial s} \frac{(1-s)^2}{s} \rightarrow \textrm{Soma série: } S_{2,\infty}\\ & = & -\frac{s}{1-s}\frac{2(-1)(1-s)s-(1-s)^2}{s^2} = \frac{2s^2+s(1-s)}{s^2} . \end{array}\]
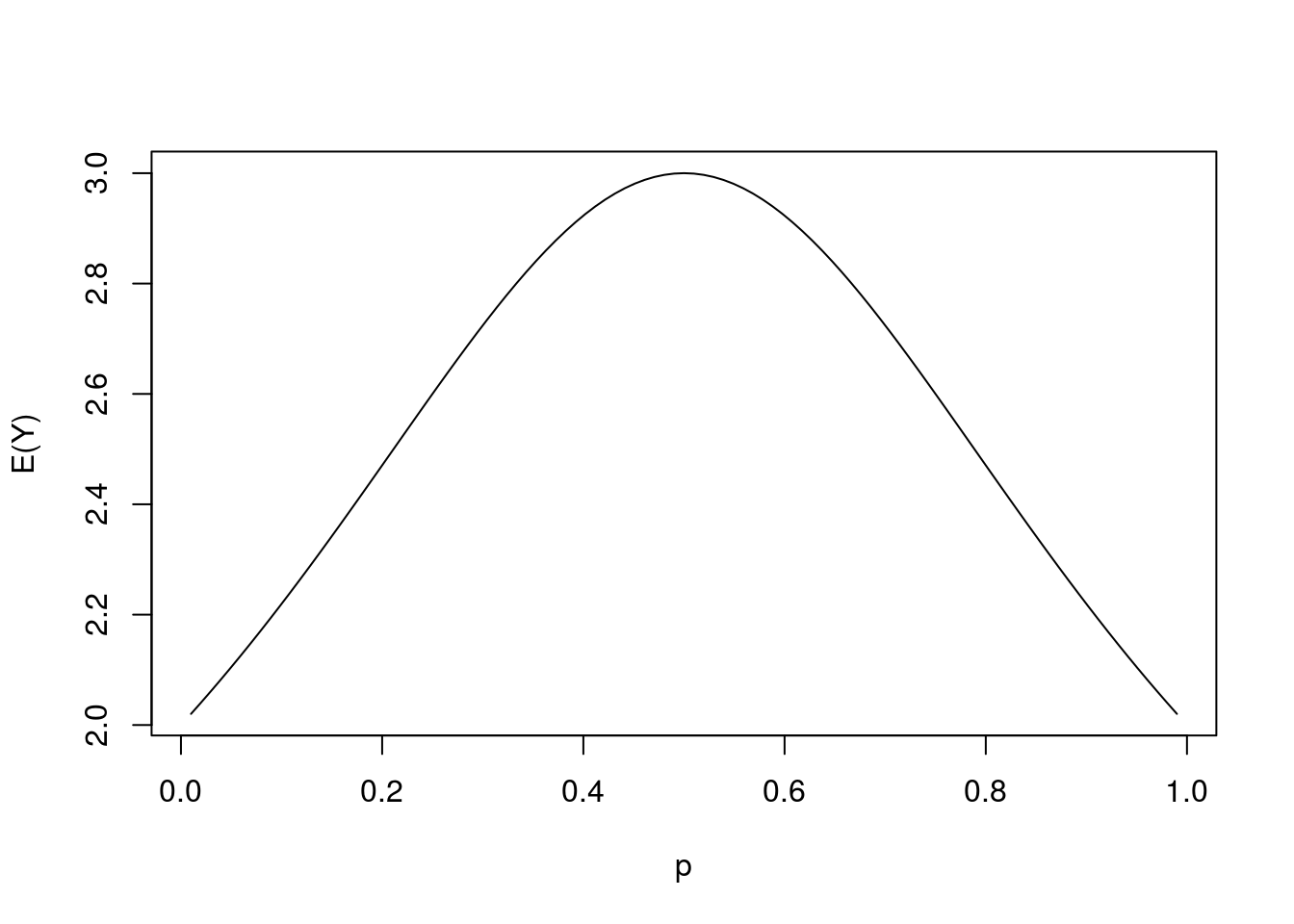
Nota-se que para \(p=1/2\) temos \(E(Y)=3\).
Adicional
Podemos ver como se comporta \(E(Y)\) em função de \(p\) na figura abaixo.
Podemos também simular esse experimento. A função abaixo pode ser usada para simular \(n\) vezes esse experimento. Mais abaixo, usamos-a para realizar o experimento uma vez e dez vezes.
rtrgeom <- function(n, p, trunc=1) {
if (trunc!=1)
stop('only works for "trunc=1"!')
ss1f <- function(p) { ### simula 1 vez
x <- rbinom(1, 1, p)
n <- 1
repeat {
y <- rbinom(1, 1, p)
n <- n + 1
if (y==x) break
x <- y
}
return(n)
}
return(replicate(n, ss1f(p)))
}
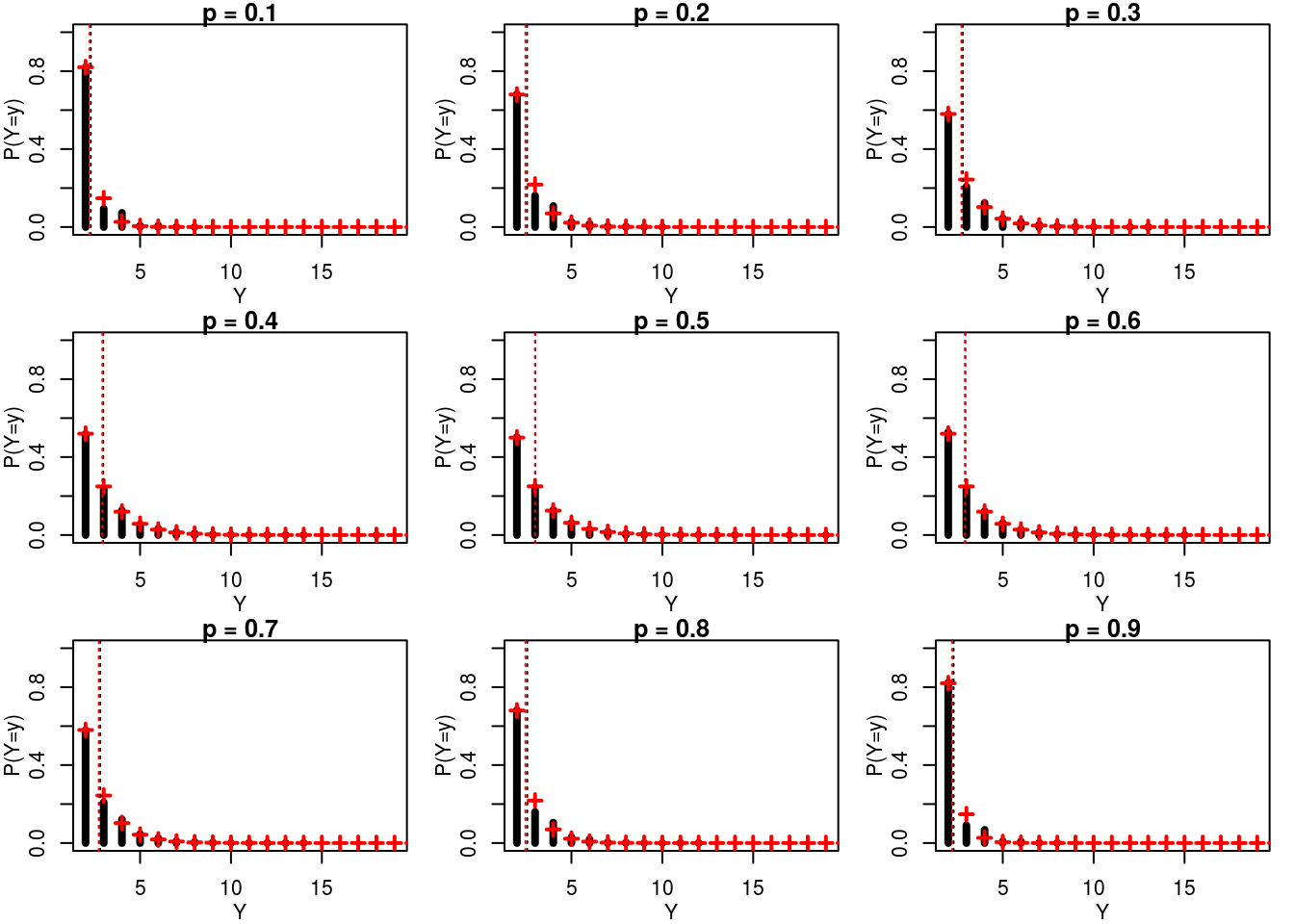
rtrgeom(1, 0.5)## [1] 2rtrgeom(10, 0.5)## [1] 3 7 2 2 2 3 2 3 2 3Vamos considerar uma sequencia de valores para \(p\), simular um número grande de experimentos e tabular o valores de \(Y\) em cada experimento. Com essas frequencias (quantas vezes \(Y=k\) ocorreu) podemos mostrar no gráfico a proporção, dividindo as frequencias pelo número de experimentos. Essa proporção é mostrada na figura abaixo (barras pretas) juntamente com o valor teórico \(P(X=k)\) (em vermelho). Além disso, temos a média observada e esperada, linhas verticais pontilhadas em preta e vermelho, respectivamente.
pseq <- seq(0.1, 0.9, 0.1); names(pseq) <- pseq
sseq <- pseq^2 + (1-pseq)^2
tt <- sapply(pseq, function(p)
table(rtrgeom(1e4, p)))
ttp <- lapply(tt, function(ttt)
list(x=as.integer(names(ttt)),
y=unclass(ttt)/sum(ttt)))
xlims <- range(unlist(lapply(ttp, head, 1)))
par(mfrow=c(3,3), mar=c(3,3,1,1), mgp=2:0)
for (j in 1:9) {
plot(ttp[[j]]$x, ttp[[j]]$y, type='h', lwd=4,
xlim=xlims, ylim=c(0,1),
main=paste0('p = ', names(tt)[j]),
xlab='Y', ylab='P(Y=y)')
points(2:50, sseq[j]*(1-sseq[j])^(0:48), col=2, pch=3, lwd=2)
abline(v=sum(as.integer(names(tt[[j]]))*tt[[j]]/sum(tt[[j]])),
lty=3)
abline(v=(2*sseq[j]^2+sseq[j]*(1-sseq[j]))/(sseq[j]^2),
lty=3, col=2)
}