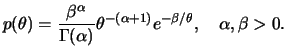A utilização de informação a priori em inferência Bayesiana
requer a especificação de uma distribuição a priori para a
quantidade de interesse ![]() . Esta distribuição deve representar
(probabilisticamente) o conhecimento que se tem sobre
. Esta distribuição deve representar
(probabilisticamente) o conhecimento que se tem sobre ![]() antes da
realização do experimento. Neste capítulo serão discutidas
diferentes formas de especificação da distribuição a priori.
antes da
realização do experimento. Neste capítulo serão discutidas
diferentes formas de especificação da distribuição a priori.
A partir do conhecimento que se tem sobre ![]() , pode-se definir uma
família paramétrica de densidades. Neste caso, a distribuição a
priori é representada por uma forma funcional, cujos parâmetros
devem ser especificados de acordo com este conhecimento. Estes
parâmetros indexadores da família de distribuições a priori são
chamados de hiperparâmetros para distingui-los dos parâmetros
de interesse
, pode-se definir uma
família paramétrica de densidades. Neste caso, a distribuição a
priori é representada por uma forma funcional, cujos parâmetros
devem ser especificados de acordo com este conhecimento. Estes
parâmetros indexadores da família de distribuições a priori são
chamados de hiperparâmetros para distingui-los dos parâmetros
de interesse ![]() .
.
Esta abordagem em geral facilita a análise e o caso mais importante é o
de prioris conjugadas. A idéia é que as distribuições a priori e a
posteriori pertençam a mesma classe de distribuições e assim a
atualização do conhecimento que se tem de ![]() envolve apenas uma
mudança nos hiperparâmetros. Neste caso, o aspecto sequencial do
método Bayesiano pode ser explorado definindo-se apenas a regra de
atualização dos hiperparâmetros já que as distribuições
permanecem as mesmas.
envolve apenas uma
mudança nos hiperparâmetros. Neste caso, o aspecto sequencial do
método Bayesiano pode ser explorado definindo-se apenas a regra de
atualização dos hiperparâmetros já que as distribuições
permanecem as mesmas.
Se
![]() é uma
classe de distribuições amostrais então uma classe de distribuições
é uma
classe de distribuições amostrais então uma classe de distribuições ![]() é conjugada a
é conjugada a ![]() se
se
Gamerman (1996, 1997 Cap. 2) alerta para o cuidado com a utilização indiscriminada de prioris conjugadas. Essencialmente, o problema é que a priori conjugada nem sempre é uma representação adequada da incerteza a priori. Sua utilização está muitas vezes associada à tratabilidade analítica decorrente.
Uma vez entendidas suas vantagens e desvantagens a questão que se coloca agora é `` como'' obter uma família de distribuições conjugadas.
Se, além disso, existe uma constante ![]() tal que
tal que
![]() e todo
e todo
![]() é definido como
é definido como
![]() então
então ![]() é a
família conjugada natural ao modelo amostral gerador de
é a
família conjugada natural ao modelo amostral gerador de
![]() .
.
Sejam
![]() Bernoulli
Bernoulli![]() . Então
a densidade amostral conjunta é
. Então
a densidade amostral conjunta é
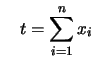
Note que
![]() é proporcional à densidade de uma distribuição
é proporcional à densidade de uma distribuição
Beta(![]() ). Além disso, se
). Além disso, se ![]() e
e ![]() são as densidades
das distribuições Beta(
são as densidades
das distribuições Beta(![]() ) e Beta(
) e Beta(![]() ) então
) então
A família exponencial inclui muitas das distribuições de probabilidade mais comumente utilizadas em Estatística, tanto contínuas quanto discretas. Uma característica essencial desta família é que existe uma estatística suficiente com dimensão fixa. Veremos adiante que a classe conjugada de distribuições é muito fácil de caracterizar.
A família de distribuições com função de (densidade) de
probabilidade
![]() pertence à família exponencial a um
parâmetro se podemos escrever
pertence à família exponencial a um
parâmetro se podemos escrever
Neste caso, a classe conjugada é facilmente identificada como,
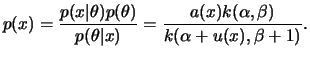
Uma extensão direta do exemplo 2..1 é o modelo binomial,
i.e.
![]() Binomial
Binomial![]() . Neste caso,
. Neste caso,
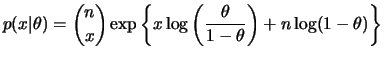
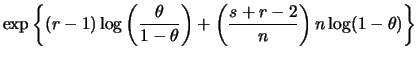 |
|||
![$\displaystyle \exp\left\{(r+x-1)\phi(\theta)+\left[\frac{s+r-2+n}{n}\right]b(\theta)\right\}$](img153.png) |
|||
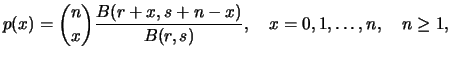
No caso geral em que se tem uma amostra
![]() da família
exponencial a natureza sequencial do teorema de Bayes permite que a
análise seja feita por replicações sucessivas. Assim a cada observação
da família
exponencial a natureza sequencial do teorema de Bayes permite que a
análise seja feita por replicações sucessivas. Assim a cada observação ![]() os parâmetros da distribuição a posteriori são
atualizados via
os parâmetros da distribuição a posteriori são
atualizados via
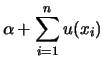 |
|||
![$\displaystyle p(\bfx) = \left[\prod_{i=1}^n
a(x_i)\right]\frac{k(\alpha,\beta)}{k(\alpha+\sum u(x_i),\beta+n)}.
$](img169.png)
Finalmente, a definição de família exponencial pode ser extendida ao caso multiparamétrico, i.e.
![$\displaystyle p(\bfx\vert\bftheta) = \left[\prod_{i=1}^n a(x_i)\right] \exp\lef...
...{j=1}^r
\left[\sum_{i=1}^n u_j(x_i)\right]\phi_j(\theta) + nb(\theta)\right\}
$](img170.png)
Já vimos que a família de distribuições Beta é conjugada ao modelo Bernoulli e binomial. Não é difícil mostrar que o mesmo vale para as distribuições amostrais geométrica e binomial-negativa. A seguir veremos resultados para outros membros importantes da família exponencial.
Para uma única observação vimos pelo teorema 1.1 que a
família de distribuições normais é conjugada ao modelo normal. Para
uma amostra de tamanho ![]() , a função de verssimilhança pode ser escrita
como
, a função de verssimilhança pode ser escrita
como
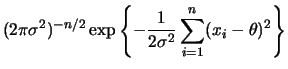 |
|||
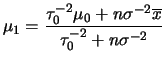 e
e
Seja
![]() uma amostra aleatória da distribuição de Poisson
com parâmetro
uma amostra aleatória da distribuição de Poisson
com parâmetro ![]() . Sua função de probabilidade conjunta é dada por
. Sua função de probabilidade conjunta é dada por
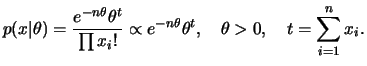
![$\displaystyle p(x\vert\theta)=\left[\prod_{i=1}^n\frac{1}{x_i!}\right]
\exp\left\{t\theta-n\theta\right\}
$](img191.png)
![$\displaystyle p(x)=\left[\prod_{i=1}^n\frac{1}{x_i!}\right]\frac{\beta^\alpha}
{\Gamma(\alpha)} \frac{\Gamma(\alpha+t)}{(\beta+n)^
{\alpha+t}}.
$](img192.png)
Denotando por
![]() o número de ocorrências em cada
uma de
o número de ocorrências em cada
uma de ![]() categorias em
categorias em ![]() ensaios independentes, e por
ensaios independentes, e por
![]() as probabilidades associadas
deseja-se fazer inferência sobre estes
as probabilidades associadas
deseja-se fazer inferência sobre estes ![]() parâmetros. No entanto,
note que existem efetivamente
parâmetros. No entanto,
note que existem efetivamente ![]() parâmetros já que temos a seguinte
restrição
parâmetros já que temos a seguinte
restrição
![]() . Além disso, a restrição
. Além disso, a restrição
![]() obviamente também se aplica. Dizemos que
obviamente também se aplica. Dizemos que ![]() tem distribuição multinomial com parâmetros
tem distribuição multinomial com parâmetros ![]() e
e ![]() e função
de probabilidade conjunta das
e função
de probabilidade conjunta das ![]() contagens
contagens ![]() é dada por
é dada por
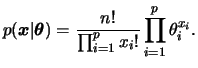
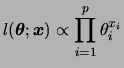
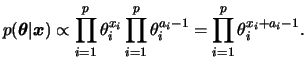
Seja
![]() uma amostra aleatória da distribuição
uma amostra aleatória da distribuição
![]() , com
, com ![]() conhecido e
conhecido e
![]() desconhecido. Neste caso a função de densidade conjunta é dada por
desconhecido. Neste caso a função de densidade conjunta é dada por
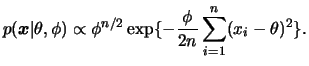
Note que o núcleo desta verossimilhança tem a mesma forma daquele de
uma distribuição Gama. Como sabemos que a família Gama é fechada por
amostragem podemos considerar uma distribuição a priori Gama com
parâmetros ![]() e
e
![]() , i.e.
, i.e.
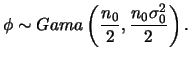
Definindo
![]() e aplicando o teorema de Bayes obtemos a distribuição a posteriori de
e aplicando o teorema de Bayes obtemos a distribuição a posteriori de
![]() ,
,
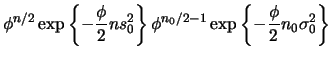 |
|||
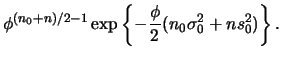 |
Note que esta expressão corresponde ao núcleo da distribuição Gama, como era esperado devido à conjugação. Portanto,
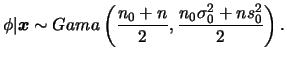
Seja
![]() uma amostra aleatória da distribuição
uma amostra aleatória da distribuição
![]() , com ambos
, com ambos ![]() e
e ![]() desconhecidos. Neste caso a distribuição a priori conjugada será
especificada em dois estágios. No primeiro estágio,
desconhecidos. Neste caso a distribuição a priori conjugada será
especificada em dois estágios. No primeiro estágio,
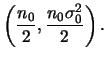
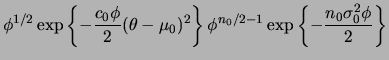 |
|||
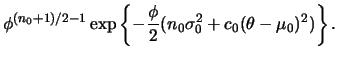 |
A partir desta densidade conjunta podemos obter a distribuição
marginal de ![]() por integração
por integração
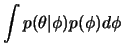 |
|||
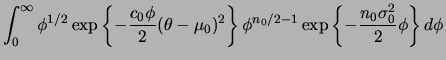 |
|||
![$\displaystyle \int_0^\infty \phi^{(n_0+1)/2-1} \exp\left\{-\frac
{\phi}{2}[n_0\sigma_0^2 + c_0(\theta-\mu_0)^2]\right\} d\phi$](img231.png) |
|||
![$\displaystyle \left[\frac{n_0\sigma_0^2 + c_0(\theta-\mu_0)^2}{2}
\right]^{-\fr...
...ft[1 + \frac{(\theta-\mu_0)^2}
{n_0(\sigma_0^2/c_0)}\right]^{-\frac{n_0+1}{2}},$](img232.png) |
![$\displaystyle \phi^{(n_0+1)/2-1} \exp\left\{-\frac{\phi}{2}[n_0\sigma_0^2 +
c_0(\theta-\mu_0)^2]\right\},$](img236.png) |
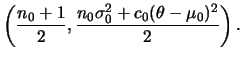
A posteriori conjunta de
![]() também é obtida em 2
etapas como segue. Primeiro, para
também é obtida em 2
etapas como segue. Primeiro, para ![]() fixo podemos usar o resultado
da seção
2.3.1 de modo que a distribuição a posteriori de
fixo podemos usar o resultado
da seção
2.3.1 de modo que a distribuição a posteriori de ![]() dado
dado ![]() fica
fica
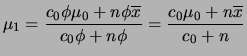 e
e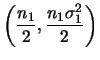
Em muitas situações é mais fácil pensar em termos de algumas
características da distribuição a priori do que em termos de
seus hiperparâmetros. Por exemplo, se
![]() ,
,
![]() ,
, ![]() e
e
![]() então
então
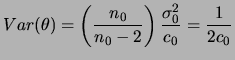
Esta seção refere-se a especificação de distribuições a priori quando se espera que a informação dos dados seja dominante, no sentido de que a nossa informação a priori é vaga. Os conceitos de `` conhecimento vago'', `` não informação'', ou `` ignorância a priori'' claramente não são únicos e o problema de caracterizar prioris com tais características pode se tornar bastante complexo.
Por outro lado, reconhece-se a necessidade de alguma forma de análise que, em algum sentido, consiga captar esta noção de uma priori que tenha um efeito mínimo, relativamente aos dados, na inferência final. Tal análise pode ser pensada como um ponto de partida quando não se consegue fazer uma elicitação detalhada do `` verdadeiro'' conhecimento a priori. Neste sentido, serão apresentadas aqui algumas formas de `` como'' fazer enquanto discussões mais detalhadas são encontradas em Berger (1985), Box e Tiao (1992), Bernardo e Smith (1994) e O'Hagan (1994).
A primeira idéia de `` não informação'' a priori que se
pode ter é pensar em todos os possíveis valores de ![]() como
igualmente prováveis, i.e., com uma distribuição a priori uniforme.
Neste caso, fazendo
como
igualmente prováveis, i.e., com uma distribuição a priori uniforme.
Neste caso, fazendo
![]() para
para ![]() variando em um
subconjunto da reta significa que nenhum valor particular tem
preferência (Bayes, 1763). Porém esta escolha de priori pode trazer
algumas dificuldades técnicas
variando em um
subconjunto da reta significa que nenhum valor particular tem
preferência (Bayes, 1763). Porém esta escolha de priori pode trazer
algumas dificuldades técnicas
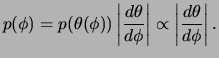
Na prática, como estaremos interessados na distribuição a posteriori não daremos muita importância à impropriedade da distribuição a priori. No entanto devemos sempre nos certificar de que a posterior é própria para antes de fazer qualquer inferência.
A classe de prioris não informativas proposta por Jeffreys (1961) é invariante a transformações 1 a 1, embora em geral seja imprópria e será definida a seguir. Antes porém precisamos da definição da medida de informação de Fisher.
Considere uma única observação ![]() com função de
(densidade) de probabilidade
com função de
(densidade) de probabilidade
![]() . A medida de informação
esperada de Fisher de
. A medida de informação
esperada de Fisher de ![]() através de
através de ![]() é definida como
é definida como
![$\displaystyle I(\theta)=E \left[-\frac{\partial^2\log
p(x\vert\theta)}{\partial\theta^2}\right]
$](img267.png)
![$\displaystyle \bfI(\bftheta)= E \left[-\frac{\partial^2\log
p(x\vert\bftheta)}{\partial\bftheta\partial\bftheta'} \right].
$](img268.png)
Note que o conceito de informação aqui está sendo associado a uma
espécie de
curvatura média da função de verossimilhança no sentido de que quanto
maior a curvatura mais precisa é a informação contida na
verossimilhança, ou equivalentemente maior o valor de
![]() . Em geral espera-se que a curvatura seja negativa e por
isso seu valor é tomado com sinal trocado. Note também que a esperança
matemática é tomada em relação à distribuição amostral
. Em geral espera-se que a curvatura seja negativa e por
isso seu valor é tomado com sinal trocado. Note também que a esperança
matemática é tomada em relação à distribuição amostral
![]() .
.
Podemos considerar então ![]() uma medida de informação
global enquanto que uma medida de informação local é obtida quando não
se toma o valor
esperado na definição acima. A medida de informação observada de
Fisher
uma medida de informação
global enquanto que uma medida de informação local é obtida quando não
se toma o valor
esperado na definição acima. A medida de informação observada de
Fisher ![]() fica então definida como
fica então definida como
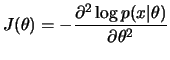
Seja uma observação ![]() com função de (densidade) de
probabilidade
com função de (densidade) de
probabilidade
![]() . A priori não informativa de Jeffreys
tem função de densidade dada por
. A priori não informativa de Jeffreys
tem função de densidade dada por
Seja
![]() Poisson
Poisson![]() . Então o
logaritmo da função de probabilidade conjunta é dado por
. Então o
logaritmo da função de probabilidade conjunta é dado por
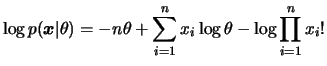
![$\displaystyle \frac{\partial^2\log p(x\vert\theta)}{\partial\theta^2}= \frac{\p...
...n+\frac{\sum_{i=1}^n x_i}{\theta}\right] =
-\frac{\sum_{i=1}^n x_i}{\theta^2}
$](img275.png)
![$\displaystyle I(\theta)=\frac{1}{\theta^2}E\left[\sum_{i=1}^n
x_i\right]=n/\theta\propto\theta^{-1}.
$](img276.png)
Em geral a priori não informativa é obtida fazendo-se o parâmetro de escala da distribuição conjugada tender a zero e fixando-se os demais parâmetros convenientemente. Além disso, a priori de Jeffreys assume formas específicas em alguns modelos que são frequentemente utilizados como veremos a seguir.
![]() tem um modelo de locação se existem uma função
tem um modelo de locação se existem uma função ![]() e
uma quantidade
e
uma quantidade ![]() tais que
tais que
![]() . Neste
caso
. Neste
caso ![]() é chamado de parâmetro de locação.
é chamado de parâmetro de locação.
A definição vale também quando ![]() é um vetor de
parâmetros. Alguns exemplos importantes são a distribuição normal com
variância conhecida, e a distribuição normal multivariada com matriz de
variância-covariância conhecida. Pode-se mostrar
que para o modelo de locação a priori de Jeffreys é dada por
é um vetor de
parâmetros. Alguns exemplos importantes são a distribuição normal com
variância conhecida, e a distribuição normal multivariada com matriz de
variância-covariância conhecida. Pode-se mostrar
que para o modelo de locação a priori de Jeffreys é dada por
![]() constante.
constante.
![]() tem um modelo de escala se existem uma função
tem um modelo de escala se existem uma função ![]() e
uma quantidade
e
uma quantidade ![]() tais que
tais que
![]() . Neste
caso
. Neste
caso ![]() é chamado de parâmetro de escala.
é chamado de parâmetro de escala.
Alguns exemplos são a distribuição exponencial com parâmetro ![]() ,
com parâmetro de escala
,
com parâmetro de escala
![]() , e a distribuição
, e a distribuição
![]() com média conhecida e escala
com média conhecida e escala ![]() . Pode-se mostrar
que para o modelo de escala a priori de Jeffreys é dada por
. Pode-se mostrar
que para o modelo de escala a priori de Jeffreys é dada por
![]() .
.
![]() tem um modelo de locação e escala se existem uma função
tem um modelo de locação e escala se existem uma função ![]() e
as quantidades
e
as quantidades ![]() e
e ![]() tais que
tais que
Alguns exemplos são a distribuição normal (uni e multivariada) e a
distribuição de Cauchy. Em modelos de locação e escala, a priori
não informativa pode ser obtida
assumindo-se independência a priori entre ![]() e
e ![]() de modo
que
de modo
que
![]() .
.
Seja
![]() com
com ![]() e
e
![]() desconhecidos. Neste caso,
desconhecidos. Neste caso,
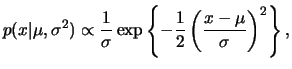
Vale notar entretanto que a priori não informativa de Jeffreys viola o princípio da verossimilhança, já que a informação de Fisher depende da distribuição amostral.
A idéia aqui é dividir a especificação da distribuição a priori em estágios. Além de facilitar a especificação esta abordagem é natural em determinadas situações experimentais.
A distribuição a priori de ![]() depende dos valores dos
hiperparâmetros
depende dos valores dos
hiperparâmetros ![]() e podemos escrever
e podemos escrever
![]() ao invés de
ao invés de
![]() . Além disso, ao invés de fixar valores para os
hiperparâmetros podemos especificar uma distribuição a priori
. Além disso, ao invés de fixar valores para os
hiperparâmetros podemos especificar uma distribuição a priori
![]() completando assim o segundo estágio na
hierarquia. A distribuição a priori marginal de
completando assim o segundo estágio na
hierarquia. A distribuição a priori marginal de ![]() pode ser
então obtida por integração como
pode ser
então obtida por integração como
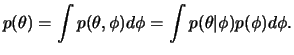
Sejam
![]() tais que
tais que
![]() com
com
![]() conhecido e queremos especificar uma distribuição a priori para o
vetor de parâmetros
conhecido e queremos especificar uma distribuição a priori para o
vetor de parâmetros
![]() . Suponha que
no primeiro estágio assumimos que
. Suponha que
no primeiro estágio assumimos que
![]() ,
,
![]() . Neste caso, se fixarmos o valor de
. Neste caso, se fixarmos o valor de
![]() e
assumirmos que
e
assumirmos que ![]() tem distribuição normal então
tem distribuição normal então ![]() terá
distribuição normal multivariada. Por outro lado, fixando um valor
para
terá
distribuição normal multivariada. Por outro lado, fixando um valor
para ![]() e assumindo que
e assumindo que ![]() tem distribuição Gama
implicará em uma distribuição
tem distribuição Gama
implicará em uma distribuição ![]() de Student multivariada para
de Student multivariada para
![]() .
.
Teoricamente, não há limitação quanto ao número de estágios, mas devido às complexidades resultantes as prioris hierárquicas são especificadas em geral em 2 ou 3 estágios. Além disso, devido à dificuldade de interpretação dos hiperparâmetros em estágios mais altos é prática comum especificar prioris não informativas para este níveis.
Uma aplicação interessante do conceito de hierarquia é quando a
informação a priori disponível só pode ser convenientemente
resumida através de uma mistura de distribuições. Isto
implica em considerar uma distribuição discreta para ![]() de modo que
de modo que
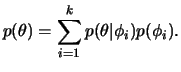
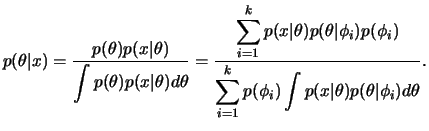
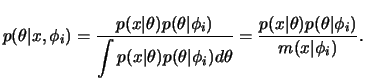
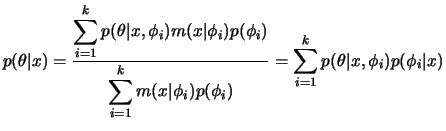
Se
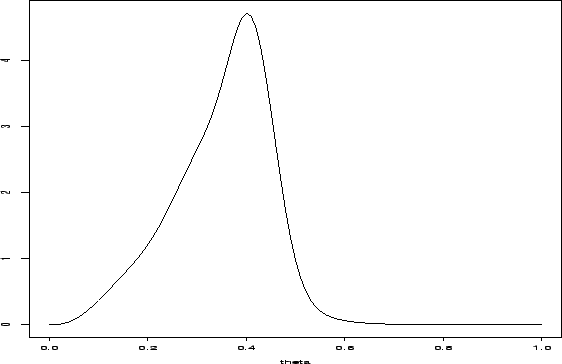
![]() , a família de distribuições a priori Beta é conveniente. Mas estas são sempre
unimodais e assimétricas à esquerda ou à direita. Outras formas interessantes, e mais
de acordo com a nossa informação a priori, podem ser obtidas
misturando-se 2 ou 3 elementos desta família. Por exemplo,
, a família de distribuições a priori Beta é conveniente. Mas estas são sempre
unimodais e assimétricas à esquerda ou à direita. Outras formas interessantes, e mais
de acordo com a nossa informação a priori, podem ser obtidas
misturando-se 2 ou 3 elementos desta família. Por exemplo,
 |
Using the Bayesian hierarchy and the prior independence assumption,
the full conditional distribution for the hyperparameter ![]() is
also easily obtained as follows,
is
also easily obtained as follows,
![$\displaystyle \left[\prod_{i=1}^k p(a_i\vert\s_a)\right] p(\s_a\vert\alpha_a,\beta_a)$](img329.png) |
|||
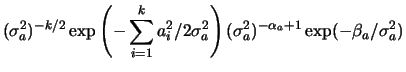 |
|||
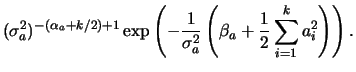 |
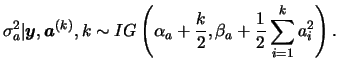 |
(2.1) |