A distribuição a posteriori de um parâmetro ![]() contém toda a
informação probabilística a respeito deste parâmetro e um gráfico da
sua função de densidade a posteriori é a melhor descrição do processo
de inferência. No entanto, algumas vezes é necessário resumir a
informação contida na posteriori através de alguns poucos valores
numéricos. O caso mais simples é a estimação pontual de
contém toda a
informação probabilística a respeito deste parâmetro e um gráfico da
sua função de densidade a posteriori é a melhor descrição do processo
de inferência. No entanto, algumas vezes é necessário resumir a
informação contida na posteriori através de alguns poucos valores
numéricos. O caso mais simples é a estimação pontual de ![]() onde
se resume a distribuição a posteriori através de um único número,
onde
se resume a distribuição a posteriori através de um único número,
![]() . Como veremos a seguir, será mais fácil entender a
escolha de
. Como veremos a seguir, será mais fácil entender a
escolha de
![]() no contexto de teoria da decisão.
no contexto de teoria da decisão.
Um problema de decisão fica completamente especificado pela descrição dos seguintes espaços:
Uma regra de decisão ![]() é uma função definida em
é uma função definida em ![]() que
assume valores em
que
assume valores em ![]() , i.e.
, i.e.
![]() . A cada
decisão
. A cada
decisão ![]() e a cada possível valor do parâmetro
e a cada possível valor do parâmetro ![]() podemos associar uma perda
podemos associar uma perda
![]() assumindo valores
positivos. Definimos assim uma função de perda.
assumindo valores
positivos. Definimos assim uma função de perda.
O risco de uma regra de decisão, denotado por ![]() ,
é a perda esperada a posteriori, i.e.
,
é a perda esperada a posteriori, i.e.
![]() .
.
Uma regra de decisão ![]() é ótima se tem risco
mínimo, i.e.
é ótima se tem risco
mínimo, i.e.
![]() . Esta regra será
denominada regra de Bayes e seu risco, risco de Bayes.
. Esta regra será
denominada regra de Bayes e seu risco, risco de Bayes.
Um laboratório farmaceutico deve decidir pelo lançamento
ou não de uma nova droga no mercado. É claro que o laboratório só
lançará a droga se achar que ela é eficiente mas isto é exatamente o
que é desconhecido. Podemos associar um parâmetro ![]() aos estados
da natureza: droga é eficiente (
aos estados
da natureza: droga é eficiente (![]() ), droga não é eficiente
(
), droga não é eficiente
(![]() ) e as possíveis ações como lança a droga (
) e as possíveis ações como lança a droga (![]() ), não
lança a droga (
), não
lança a droga (![]() ). Suponha que foi possível construir a seguinte tabela de
perdas levando em conta a eficiência da droga,
). Suponha que foi possível construir a seguinte tabela de
perdas levando em conta a eficiência da droga,
| eficiente | não eficiente | |
| lança | -500 | 600 |
| não lança | 1500 | 100 |
Vale notar que estas perdas traduzem uma avaliação subjetiva em
relação à gravidade dos erros cometidos. Suponha agora que a incerteza
sobre os estados da natureza é descrita por
![]() ,
,
![]() avaliada na distribuição atualizada de
avaliada na distribuição atualizada de ![]() (seja a
priori ou a posteriori). Note que, para
(seja a
priori ou a posteriori). Note que, para ![]() fixo,
fixo,
![]() é uma variável aleatória discreta assumindo apenas
dois valores com probabilidades
é uma variável aleatória discreta assumindo apenas
dois valores com probabilidades ![]() e
e ![]() . Assim, usando a
definição de risco obtemos que
. Assim, usando a
definição de risco obtemos que
Seja agora uma amostra aleatória
![]() tomada de uma
distribuição com função de (densidade) de probabilidade
tomada de uma
distribuição com função de (densidade) de probabilidade
![]() aonde o valor do parâmetro
aonde o valor do parâmetro ![]() é desconhecido. Em um problema de
inferência como este o valor de
é desconhecido. Em um problema de
inferência como este o valor de ![]() deve ser estimado a partir
dos valores observados na amostra.
deve ser estimado a partir
dos valores observados na amostra.
Se
![]() então é
razoável que os possíveis valores de um estimador
então é
razoável que os possíveis valores de um estimador
![]() também devam pertencer ao espaço
também devam pertencer ao espaço ![]() . Além disso, um bom
estimador é aquele para o qual, com alta probabilidade, o erro
. Além disso, um bom
estimador é aquele para o qual, com alta probabilidade, o erro
![]() estará próximo de zero. Para cada possível valor
de
estará próximo de zero. Para cada possível valor
de ![]() e cada possível estimativa
e cada possível estimativa
![]() vamos
associar uma perda
vamos
associar uma perda
![]() de modo que quanto maior a distância
entre
de modo que quanto maior a distância
entre ![]() e
e ![]() maior o valor da perda. Neste caso, a perda
esperada a posteriori é dada por
maior o valor da perda. Neste caso, a perda
esperada a posteriori é dada por
![$\displaystyle E[L(a,\theta)\vert\bfx] = \int L(a,\theta)p(\theta\vert\bfx) d\theta
$](img414.png)
Aqui vamos discutir apenas funções de perda simétricas, já que estas
são mais comumente utilizadas. Dentre estas a mais utilizada em
problemas de estimação é certamente a função de perda quadrática,
definida como
![]() . Neste caso, pode-se mostrar
que o estimador de Bayes para o parâmetro
. Neste caso, pode-se mostrar
que o estimador de Bayes para o parâmetro ![]() será a média de sua
distribuição atualizada.
será a média de sua
distribuição atualizada.
Suponha que queremos estimar a proporção
![]() de itens
defeituosos em um grande lote. Para isto será tomada uma amostra aleatória
de itens
defeituosos em um grande lote. Para isto será tomada uma amostra aleatória
![]() de uma distribuição de Bernoulli com parâmetro
de uma distribuição de Bernoulli com parâmetro
![]() . Usando uma priori conjugada Beta(
. Usando uma priori conjugada Beta(
![]() ) sabemos que
após observar a amostra a distribuição a posteriori é
Beta(
) sabemos que
após observar a amostra a distribuição a posteriori é
Beta(
![]() ) onde
) onde
![]() . A média desta
distribuição Beta é dada por
. A média desta
distribuição Beta é dada por
![]() e portanto
o estimador de Bayes de
e portanto
o estimador de Bayes de ![]() usando perda quadrática é
usando perda quadrática é
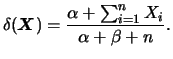
A perda quadrática é as vezes criticada por penalizar demais o erro de
estimação. A função de perda absoluta, definida como
![]() , introduz punições que crescem linearmente
com o erro de estimação e pode-se mostrar que o estimador de Bayes
associado é a mediana da distribuição atualizada de
, introduz punições que crescem linearmente
com o erro de estimação e pode-se mostrar que o estimador de Bayes
associado é a mediana da distribuição atualizada de ![]() .
.
Para reduzir ainda mais o efeito de erros de estimação grandes podemos considerar funções que associam uma perda fixa a um erro cometido, não importando sua magnitude. Uma tal função de perda, denominada perda 0-1, é definida como
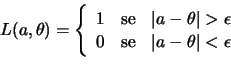
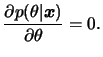
Se
![]() é uma amostra aleatória da
é uma amostra aleatória da
![]() com
com
![]() conhecido e usarmos a priori conjugada, i.e.
conhecido e usarmos a priori conjugada, i.e.
![]() então a posteriori também será normal e neste caso
média, mediana e moda coincidem. Portanto, o estimador de Bayes de
então a posteriori também será normal e neste caso
média, mediana e moda coincidem. Portanto, o estimador de Bayes de
![]() é dado por
é dado por
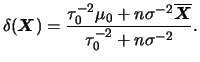
No exemplo 3..2 suponha que foram observados 100
itens dos quais 10 eram defeituosos. Usando perda quadrática a
estimativa de Bayes de ![]() é
é
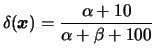
Voltamos a enfatizar que a forma mais adequada de expressar a informação que se tem sobre um parâmetro é através de sua distribuição a posteriori. A principal restrição da estimação pontual é que quando estimamos um parâmetro através de um único valor numérico toda a informação presente na distribuição a posteriori é resumida através deste número. É importante também associar alguma informação sobre o quão precisa é a especificação deste número. Para os estimadores vistos aqui as medidas de incerteza mais usuais são a variância ou o coeficiente de variação para a média a posteriori, a medida de informação observada de Fisher para a moda a posteriori, e a distância entre quartis para a mediana a posteriori.
Nesta seção vamos introduzir um compromisso entre o uso da própria distribuição a posteriori e uma estimativa pontual. Será discutido o conceito de intervalo de credibilidade (ou intervalo de confiança Bayesiano) baseado no distribuição a posteriori.
C é um intervalo de credibilidade de 100(1-![]() )%,
ou nível de credibilidade (ou confiança)
)%,
ou nível de credibilidade (ou confiança) ![]() , para
, para ![]() se
se
![]() .
.
Note que a definição expressa de forma probabilística a pertinência ou
não de ![]() ao intervalo. Assim, quanto menor for o tamanho do
intervalo mais concentrada é a distribuição do parâmetro, ou seja o
tamanho do intervalo informa sobre a dispersão de
ao intervalo. Assim, quanto menor for o tamanho do
intervalo mais concentrada é a distribuição do parâmetro, ou seja o
tamanho do intervalo informa sobre a dispersão de ![]() . Além
disso, a exigência de que a probabilidade acima possa ser maior do
que o nível de confiança é essencialmente técnica pois queremos que o
intervalo seja o menor possível, o que em geral implica em usar uma
igualdade. No entanto, a desigualdade será útil se
. Além
disso, a exigência de que a probabilidade acima possa ser maior do
que o nível de confiança é essencialmente técnica pois queremos que o
intervalo seja o menor possível, o que em geral implica em usar uma
igualdade. No entanto, a desigualdade será útil se ![]() tiver uma
distribuição discreta onde nem sempre é possível satisfazer a
igualdade.
tiver uma
distribuição discreta onde nem sempre é possível satisfazer a
igualdade.
Outro fato importante é que os intervalos de credibilidade são
invariantes a transformações 1 a 1,
![]() . Ou seja, se
. Ou seja, se ![]() é um intervalo de credibilidade 100(1-
é um intervalo de credibilidade 100(1-![]() )% para
)% para ![]() então
então
![]() é um intervalo de credibilidade 100(1-
é um intervalo de credibilidade 100(1-![]() )%
para
)%
para
![]() . Note que esta propriedade também vale para
intervalos de confiança na inferência clássica.
. Note que esta propriedade também vale para
intervalos de confiança na inferência clássica.
É possível construir uma infinidade de intervalos usando a definição
acima mas estamos interessados apenas naquele com o menor
comprimento possível. Pode-se mostrar que intervalos de comprimento
mínimo são obtidos tomando-se os valores de ![]() com maior
densidade a posteriori, e esta idéia é expressa matematicamente na
definição abaixo.
com maior
densidade a posteriori, e esta idéia é expressa matematicamente na
definição abaixo.
Um intervalo de credibilidade ![]() de 100(1-
de 100(1-![]() )%
para
)%
para ![]() é de máxima densidade a posteriori (MDP) se
é de máxima densidade a posteriori (MDP) se
![]() onde
onde ![]() é a maior constante tal que
é a maior constante tal que
![]() .
.
Usando esta definição, todos os pontos dentro do intervalo MDP terão
densidade maior do que qualquer ponto fora do intervalo. Além disso,
no caso de distribuições com duas caudas, e.g. normal, ![]() de Student,
o intervalo MDP é obtido de modo que as caudas tenham a mesma
probabilidade.
de Student,
o intervalo MDP é obtido de modo que as caudas tenham a mesma
probabilidade.
Um problema com os intervalos MDP é que eles não são invariantes a transformações 1 a 1, a não ser para transformações lineares. O mesmo problema ocorre com intervalos de comprimento mínimo na inferência clássica.
Os resultados desenvolvidos nos capítulos anteriores serão aplicados ao modelo normal para estimação da média e variância em problemas de uma ou mais amostras e em modelos de regressão linear. A análise será feita com priori conjugada e priori não informativa quando serão apontadas as semelhanças com a análise clássica. Assim como nos capítulos anteriores a abordagem aqui é introdutória. Um tratamento mais completo do enfoque Bayesiano em modelos lineares pode ser encontrado em Broemeling (1985) e Box e Tiao (1992).
Nesta seção considere uma amostra aleatória
![]() tomada da distribuição
tomada da distribuição
![]() .
.
Se ![]() é conhecido e a priori de
é conhecido e a priori de ![]() é
é
![]() então,
pelo Teorema 1.1, a posteriori de
então,
pelo Teorema 1.1, a posteriori de ![]() é
é
![]() .
Intervalos de confiança Bayesianos para
.
Intervalos de confiança Bayesianos para ![]() podem então ser construídos usando o fato de que
podem então ser construídos usando o fato de que
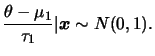
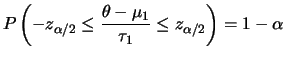
A priori não informativa pode ser obtida fazendo-se a variância da
priori tender a infinito, i.e.
![]() . Neste caso, é fácil verificar que
. Neste caso, é fácil verificar que
![]() e
e
![]() , i.e. a média e a precisão da
posteriori convergem para a média e a precisão amostrais. Média, moda e
mediana a posteriori coincidem então com a estimativa clássica de máxima
verossimilhança,
, i.e. a média e a precisão da
posteriori convergem para a média e a precisão amostrais. Média, moda e
mediana a posteriori coincidem então com a estimativa clássica de máxima
verossimilhança,
![]() . O intervalo de confiança
Bayesiano 100(1-
. O intervalo de confiança
Bayesiano 100(1-![]() )% é dado por
)% é dado por
Neste caso, usando a priori conjugada
Normal-Gama vista no Capítulo 2 temos que a
distribuição a posteriori marginal de ![]() é dada por
é dada por
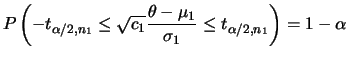
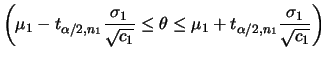
No caso da variância populacional ![]() intervalos de confiança
podem ser obtidos usando os
percentis da distribuição qui-quadrado uma vez que a distribuição
a posteriori de
intervalos de confiança
podem ser obtidos usando os
percentis da distribuição qui-quadrado uma vez que a distribuição
a posteriori de ![]() é tal que
é tal que
![]() . Denotando por
. Denotando por
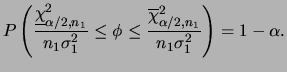
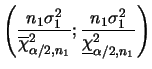
Um caso particular é quanto utilizamos uma priori não
informativa. Vimos na Seção 2.4 que a priori não
informativa de locação e escala é
![]() ,
portanto pela propriedade de invariância segue que
a priori não informativa de
,
portanto pela propriedade de invariância segue que
a priori não informativa de
![]() é obtida fazendo-se
é obtida fazendo-se
![]() . Note que este é um caso particular (degenerado) da priori conjugada
natural com
. Note que este é um caso particular (degenerado) da priori conjugada
natural com ![]() ,
,
![]() e
e ![]() . Neste caso a
distribuição a posteriori
marginal de
. Neste caso a
distribuição a posteriori
marginal de ![]() fica
fica
Mais uma vez média, moda e mediana a posteriori de ![]() coincidem com
a média amostral
coincidem com
a média amostral
![]() que é a estimativa de máxima
verossimilhança. Como
que é a estimativa de máxima
verossimilhança. Como
![]() segue que o intervalo de confiança 100(1-
segue que o intervalo de confiança 100(1-![]() )% para
)% para ![]() de MDP
é
de MDP
é
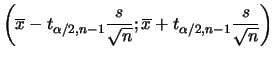
Para fazer inferências sobre ![]() temos que
temos que
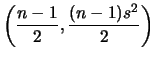 ou
ou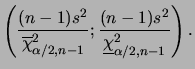
Mais uma vez vale enfatizar que esta coincidência com as estimativas clássicas é apenas numérica uma vez que as interpretações dos intervalos diferem radicalmente.
Nesta seção vamos assumir que
![]() e
e
![]() são
amostras aleatórias das distribuições
são
amostras aleatórias das distribuições
![]() e
e
![]() respectivamente e que as amostras são
independentes.
respectivamente e que as amostras são
independentes.
Para começar vamos assumir que as variâncias ![]() e
e ![]() são
conhecidas. Neste caso, a função de verossimilhança é dada por
são
conhecidas. Neste caso, a função de verossimilhança é dada por
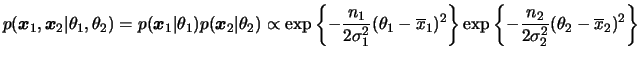
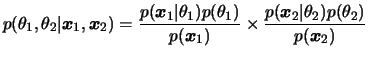
Se usarmos a classe de prioris conjugadas
![]() então as posterioris independentes serão
então as posterioris independentes serão
![]() onde
onde
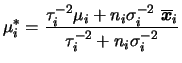 e
e
Em geral estaremos interessados em comparar as médias populacionais,
i.e queremos estimar
![]() . Neste caso, a
posteriori de
. Neste caso, a
posteriori de ![]() é facilmente obtida, devido à independência, como
é facilmente obtida, devido à independência, como
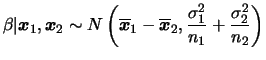
No caso de variâncias populacionais desconhecidas porém iguais,
temos que
![]() . A priori conjugada pode ser
construída em duas etapas. No primeiro estágio, assumimos que, dado
. A priori conjugada pode ser
construída em duas etapas. No primeiro estágio, assumimos que, dado
![]() ,
, ![]() e
e ![]() são a priori condicionalmente
independentes, e especificamos
são a priori condicionalmente
independentes, e especificamos
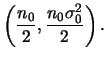
![$\displaystyle \phi^{n_0/2}
\exp\left\{-\frac{\phi}{2}
\bigg[n_0\s_0+c_1(\theta_1-\mu_1)^2+c_2(\theta_2-\mu_2)^2
\bigg]\right\}.$](img505.png) |
Além disso, também não é difícil obter a priori condicional de
![]() , dado
, dado ![]() , como
, como
Podemos mais uma vez obter a posteriori conjunta em duas etapas já que
![]() e
e ![]() também serão condicionalmente independentes a
posteriori, dado
também serão condicionalmente independentes a
posteriori, dado ![]() . Assim, no primeiro estágio usando os
resultados obtidos anteriormente para uma amostra segue que
. Assim, no primeiro estágio usando os
resultados obtidos anteriormente para uma amostra segue que
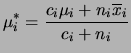 e
e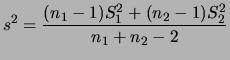
![$\displaystyle p(\bfx_1,\bfx_2\vert\theta_1,\theta_2,\phi)=
\phi^{(n_1+n_2)/2}
\...
...\theta_1-\overline{\bfx}_1)^2+n_2(\theta_2-\overline{\bfx}_2)^2
\bigg]\right\}
$](img513.png)
![$\displaystyle \phi^{(n_0+n_1+n_2)/2}
\exp\left\{-\frac{\phi}{2}\bigg[n_0\s_0+\n...
...}{c_i^*}(\mu_i-\overline{\bfx}_i)^2+
c_i^*(\theta_i-\mu_i^*)^2
\bigg]\right\}.
$](img514.png)
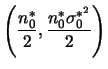
Assim, média, moda e mediana a posteriori de ![]() coincidem e a
estimativa pontual é
coincidem e a
estimativa pontual é
![]() . Também intervalos de
credibilidade de MDP podem ser obtidos usando os percentis da
distribuição
. Também intervalos de
credibilidade de MDP podem ser obtidos usando os percentis da
distribuição ![]() de Student. Para a variância populacional a estimativa
pontual usual é
de Student. Para a variância populacional a estimativa
pontual usual é
![]() e intervalos podem ser construídos
usando os percentis da distribuição qui-quadrado já que
e intervalos podem ser construídos
usando os percentis da distribuição qui-quadrado já que
![]()
Vejamos agora como fica a análise usando priori não informativa. Neste
caso,
![]() e isto equivale a um
caso particular (degenerado) da priori conjugada com
e isto equivale a um
caso particular (degenerado) da priori conjugada com ![]() ,
,
![]() e
e ![]() . Assim, temos que
. Assim, temos que ![]() ,
,
![]() ,
, ![]() e
e
![]() e a estimativa pontual concide com a estimativa de máxima
verossimilhança
e a estimativa pontual concide com a estimativa de máxima
verossimilhança
![]() . O
intervalo de
. O
intervalo de
![]() de MDP para
de MDP para ![]() tem limites
tem limites
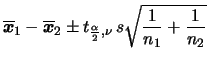
O intervalo de
![]() para
para ![]() é obtido de maneira análoga
ao caso de uma amostra usando a distribuição qui-quadrado, agora com
é obtido de maneira análoga
ao caso de uma amostra usando a distribuição qui-quadrado, agora com
![]() graus de liberdade, i.e.
graus de liberdade, i.e.
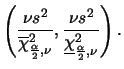
Até agora assumimos que as variâncias populacionais desconhecidas eram
iguais (ou pelo menos aproximadamente iguais). Na inferência clássica
a violação desta
suposição leva a problemas teóricos e práticos uma vez que não é
trivial encontrar uma quantidade pivotal para ![]() com distribuição
conhecida ou tabelada. Na verdade, se existem grandes diferenças de
variabilidade
entre as duas populações pode ser mais apropriado analisar
conjuntamente as consequências das diferenças entre as médias e as
variâncias. Assim, caso o pesquisador tenha interesse no parâmetro
com distribuição
conhecida ou tabelada. Na verdade, se existem grandes diferenças de
variabilidade
entre as duas populações pode ser mais apropriado analisar
conjuntamente as consequências das diferenças entre as médias e as
variâncias. Assim, caso o pesquisador tenha interesse no parâmetro
![]() deve levar em conta os problemas de ordem teóricas
introduzidos por uma diferença substancial entre
deve levar em conta os problemas de ordem teóricas
introduzidos por uma diferença substancial entre ![]() e
e ![]() .
.
Do ponto de vista Bayesiano o que precisamos fazer é combinar informação a priori com a verossimilhança e basear a estimação na distribuição a posteriori. A função de verossimilhança agora pode ser fatorada como
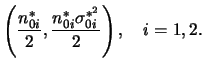
Outra situação de interesse é a comparação das duas variâncias
populacionais. Neste caso, faz mais sentido utilizar a razão de
variâncias ao invés da diferença já que elas medem a escala de uma
distribuição e são sempre positivas. Neste caso temos que obter a
distribuição a posteriori de
![]() . Usando a
independência a posteriori de
. Usando a
independência a posteriori de ![]() e
e ![]() e após algum
algebrismo pode-se mostrar que
e após algum
algebrismo pode-se mostrar que
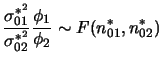
Embora sua função de distribuição não possa ser obtida analiticamente os valores estão tabelados em muitos livros de estatística e também podem ser obtidos na maioria dos pacotes computacionais. Os percentis podem então ser utilizados na construção de intervalos de credibilidade para a razão de variâncias.
Uma propriedade bastante útil para calcular probabilidade com a
distribuição ![]() vem do fato de que se
vem do fato de que se
![]() então
então
![]() por simples inversão na razão de
distribuições qui-quadrado independentes. Assim, denotando os quantis
por simples inversão na razão de
distribuições qui-quadrado independentes. Assim, denotando os quantis
![]() e
e ![]() da distribuição
da distribuição
![]() por
por
![]() e
e
![]() respectivamente segue que
respectivamente segue que
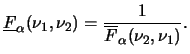
Finalmente, a análise usando priori não informativa pode ser feita
para
![]() e será
deixada como exercício.
e será
deixada como exercício.