Abstract
The mglm4twin package implements multivariate
generalized linear models for twin and family data as proposed by Bonat
and Hjelmborg (2020). The core fit function mglm4twin is
employed for fitting a set of models. In this introductory vignette we
restrict ourselves to model continuous outcomes. We present a set of
special specifications of the standard ACE for continuous (Gaussian)
trait in the context of twin data. This vignette reproduces the data
analysis presented in the Section 5.2 Dataset 2: Continuous data of
Bonat and Hjelmborg (2020).
Install and loading the mglm4twin package
To install the stable version of mglm4twin,
use devtools::install_git(). For more information, visit mglm4twin/README.
library(devtools)
install_git("bonatwagner/mglm4twin")
library(mglm4twin)
packageVersion("mglm4twin")
#> [1] '0.5.0'Data set
This example regards a fairly common continuous trait analysis. The
dataset is part of the twinbmidataset from the
metspackage. In this vignette, we restrict our attention to
a subset of the original data set where we have paired observation for
both twin. The resulting dataset consists of 4271 (2788 DZ and 1483 MZ)
twin-pairs. The analysis goal is to investigate the genetic and common
environment influences on the body mass index (BMI).
Model specification
The model specification is done in three steps:
- Specifying the linear predictor (mean model).
- Specifying the matrix linear predictor (twin dependence struture).
- Specifying link and variance function suitable to be response variable type.
Specyfing the linear predictor
The linear predictor was composed of the interactive effect between
zygosity (Group) (DZ and MZ) and twin pair
(Twin_pair) code (Twin 1 and Twin 2). Thus, the linear
predictor is given by
linear_pred <- bmi ~ Group*Twin_pairSpecyfing the matrix linear predictor
The matrix linear predictor describes the twin dependence structure.
The mglm4twin package provides a set of pre-specified
covariance structures. The matrix linear predictor is a linear
combination of known matrices. This specification allows for an easy and
flexible specification of the covariance structure including the
possibility to model each of the dispersion components as a linear
function of known covariates. In this example, we model the dispersion
components for the ACE model as a function of age and gender. Let’s
start specifying the standard ACE and AE models.
ACE = mt_twin(N_DZ = 5576/2, N_MZ = 2966/2, n_resp = 1, model = "ACE")
AE = mt_twin(N_DZ = 5576/2, N_MZ = 2966/2, n_resp = 1, model = "AE")For specifying the linear models for the dispersion components the
mglm4twinpackage provides a an interface similar to the
glm() using formulas. Let’s standardized the covariate age
to avoid numerical issues and then specify the formula for each of the
ACE model’s components.
bmi$age <- (bmi$age - mean(bmi$age))/sd(bmi$age)
list_form <- list(formE = ~ age + gender, formA = ~ age + gender,
formC = ~ age + gender)By using this set of formula we can specify the matrix linear
predictor for the ACE model. Note that, now we are using the argument
formula where we pass a list of formulas.
ACE_reg = mt_twin(N_DZ = 5576/2, N_MZ = 2966/2, n_resp = 1,
model = "ACE", formula = list_form, data = bmi)We can restrict the more general ACE model to its special cases as
for example the AE model where the components A and E are modelled as a
function of age and gender.
Specyfing link and variance functions
The specification of the link and variance functions depends on the
response variable type. In the case of the continuous and symmetric data
the standard choice is the identity function. For the
variance function the constant represents the standard
Gaussian variance function, which is suitable for continuous and
symmetric outcomes. In this example, we follow Bonat and Hjelmborg
(2020) and use the identity link function and the
constant variance function. It is important to note that
these choices are the default approach in the
mglm4twin()function.
link = "identity"
variance = "constant"Model fitting
The next step is fitting the specified models.
## Standard ACE model
fit_ACE <- mglm4twin(linear_pred = c(linear_pred),
matrix_pred = ACE, data = bmi)
#> Automatic initial values selected.
## Standard AE model
fit_AE <- mglm4twin(linear_pred = c(linear_pred),
matrix_pred = AE, data = bmi)
#> Automatic initial values selected.
## ACE regression on the dispersion
fit_ACE_reg <- mglm4twin(linear_pred = c(linear_pred),
matrix_pred = ACE_reg, data = bmi)
#> Automatic initial values selected.
## AE regression on the dispersion
fit_AE_reg <- mglm4twin(linear_pred = c(linear_pred),
matrix_pred = AE_reg, data = bmi)
#> Automatic initial values selected.Model output
In this example, there are a lot of dispersion components and model
selection is required to simplify the model by dropping non-significant
components. The mglm4twin package offers a set of functions
to assist in this process. The mt_anova_mglm()function
performs an ANOVA-type test for the dispersion components in each of the
ACE model components.
mt_anova_mglm(fit_ACE_reg, formula = list_form, data = bmi)
#> Wald test for dispersion components
#> Call: $formE
#> ~age + gender
#>
#> $formA
#> ~age + gender
#>
#> $formC
#> ~age + gender
#>
#>
#> Covariate Chi.Square Df p.value
#> 1 formE 824.7110 3 0.0000000
#> 2 formA 191.3678 3 0.0000000
#> 3 formC 3.3677 3 0.3383316The results show that estimates involved in the C component are non-significant. Thus, we simplify the model to the AE. Checking the significance of the AE model’s components.
mt_anova_mglm(fit_AE_reg, formula = list_form2, data = bmi)
#> Wald test for dispersion components
#> Call: $formE
#> ~age + gender
#>
#> $formA
#> ~age + gender
#>
#>
#> Covariate Chi.Square Df p.value
#> 1 formE 790.9315 3 0
#> 2 formA 1017.7857 3 0The results show that in this case all estimates of the E and A are
jointly significant. We can further explore the significance of the
components by looking at each one. When using
type = robust2 it can take long that’s why we do not run
this code while building the package, but the user can run without
problems.
aux_summary(fit_AE_reg, formula = list_form2,
type = "robust2", id = bmi$Twin, data = bmi)The results show that the A dispersion component associate to the age is non-significant. Thus, we can specify an AE simplified model by dropping this component.
list_form3 <- list(formE = ~ age + gender, formA = ~ gender)
AE_reg1 = mt_twin(N_DZ = 5576/2, N_MZ = 2966/2, n_resp = 1,
model = "AE", formula = list_form3, data = bmi)
fit_AE_reg1 <- mglm4twin(linear_pred = c(linear_pred), matrix_pred = AE_reg1,
data = bmi)
#> Automatic initial values selected.Standard output
For complex model as the ones with covariates describing the
dispersion structure the mglm4twin package does not offer
standard model’s output like summary(). Thus, the users
have to extract the componets and build the output themselves.
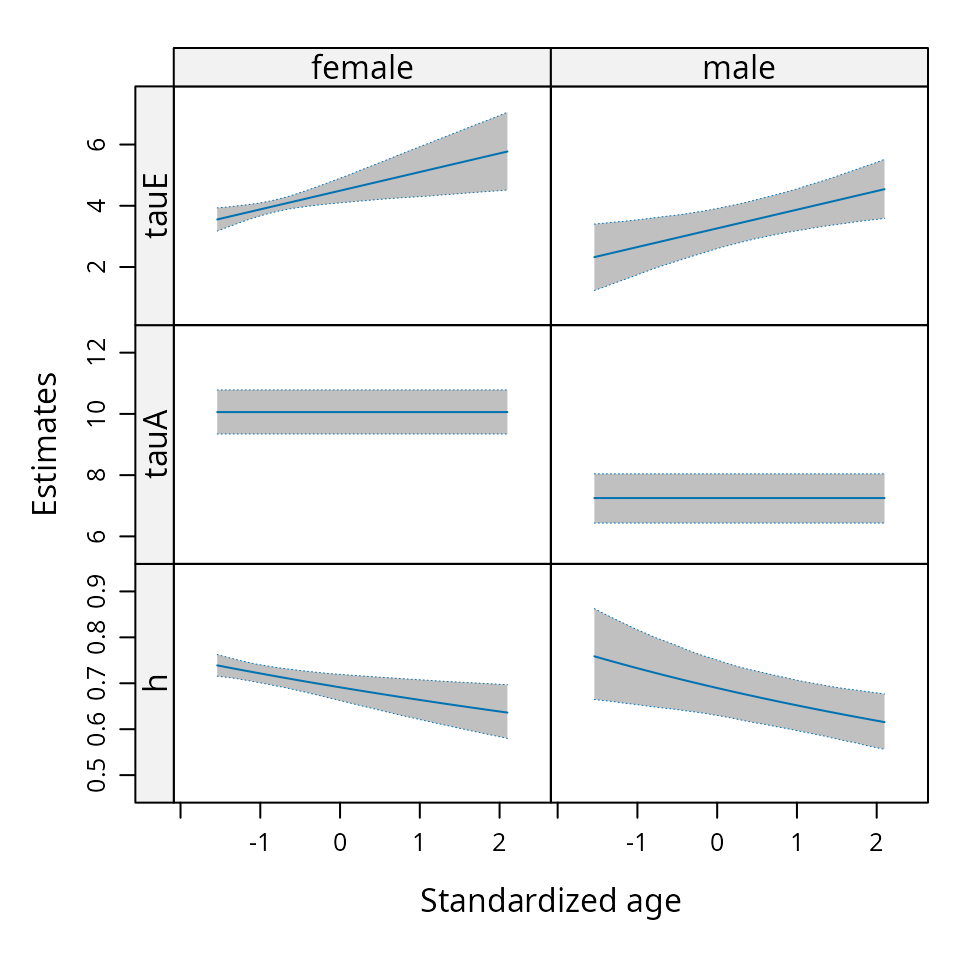
Reproducing Table 2 of Bonat and Hjelmborg (2020)
Table2
#> Parameters ACE_reg std_ACE_reg AE_reg std_AE_reg AE_reg1 std_AE_reg1
#> 1 E0 4.53 0.21 4.45 0.20 4.50 0.20
#> 2 E_age 0.44 0.15 0.49 0.14 0.61 0.12
#> 3 E_gender -1.28 0.28 -1.21 0.26 -1.23 0.26
#> 4 A0 9.26 0.75 10.11 0.37 10.05 0.37
#> 5 A_age 0.90 0.51 0.40 0.25 NA NA
#> 6 A_gender -2.11 0.98 -2.81 0.48 -2.80 0.48
#> 7 C0 0.84 0.64 NA NA NA NA
#> 8 C_age -0.48 0.43 NA NA NA NA
#> 9 C_gender -0.69 0.83 NA NA NA NA
#> 10 plogLik(df) -22293.07 13.00 -22294.71 10.00 -22295.88 9.00
#> 11 pAIC 44612.14 NA 44609.42 NA 44609.76 NA