Capítulo 1 Introdução
Correlação e regressão estão intimamente relacionadas. Na correlação estamos principalmente preocupados com os aspectos qualitativos das relações possíveis. A regressão preocupa-se com os aspectos quantitativos das relações, tais como determinar a inclinação e intercepto de uma linha reta que fornece um ajuste adequado para dados fornecidos. Caso o ajuste considerado adequado seja um polinômio de grau \(p\) é necessário fornecer valores para as \(p+1\) constantes que determinam um polinômio de melhor ajuste. Há sim equivalência entre alguns aspectos das duas abordagens, por exemplo, em regressão linear um teste de inclinação zero é equivalente a um teste de correlação zero. Valores de +1 ou -1 para o coeficiente de correlação do produto de momentos da Pearson nos diz que todos os pontos observados estão em uma linha reta.
Estudaremos aqui a regressão não paramétrica e para isso vamos considerar \(n\) pares de observações \((x_1,Y_1),\cdots,(x_n,Y_n)\) como nas figuras abaixo. A variável aleatória resposta \(Y\) está relacionada à covariável determinística \(x\) pelas equações \[\begin{equation} Y_i \, = \, r(x_i)+\epsilon_i, \qquad \mbox{E}(\epsilon_i) \, = 0, \qquad i=1,2,\cdots,n, \end{equation}\] onde \(r\) é a função de regressão. A variável \(x\) também é chamada de recurso.
Queremos estimar ou “aprender” a função \(r\) em hipóteses fracas. O estimador de \(r(x)\) é denotado por \(\widehat{r}_n(x)\). Também nos referimos a \(\widehat{r}_n(x)\) como um suavizador. A princípio, faremos a suposição simplificadora de que a variância \(\mbox{Var}(\epsilon_i) = \sigma^2\), ou seja, a variância de \(\epsilon_i\) não depende de \(x\). Vamos relaxar essa suposição mais tarde.
Na equação acima, estamos tratando os valores da covariável \(x_i\) como fixos. Poderíamos tratá-los como aleatórios, em cujo caso escrevemos os dados como \((X_1,Y_1),\cdots,(X_n,Y_n)\) e \(r(x)\) é então interpretado como a média de \(Y\) condicional em \(X = x\), isto é, \[\begin{equation} r(x) \, = \, \mbox{E}(Y \,| \, X=x)\cdot \end{equation}\] Há pouca diferença nas duas abordagens e, na maioria das vezes, adotamos a abordagem “fixo \(x\)”, exceto quando indicado.
Exemplo 1.
Começamos com um conjunto de dados clássico retirado do livro de Pagan & Ullah (1999). Eles consideram dados salariais canadenses consistindo de uma amostra aleatória retirada das cópias de uso público do Censo Canadense de 1971 para indivíduos do sexo masculino com educação em comum (Grau 13).
Existem \(n = 205\) observações no total e 2 variáveis: o logaritmo do salário do indivíduo (logwage) e sua idade (age). A equação salarial tradicional é tipicamente modelada como uma idade quadrática. Os dados estão disponíveis no arquivo de dados cps71, no pacote de funções np. Este será um dos pacotes de funções R que utilizaremos para mostrar o ajuste dos modelos de regressão não paramétricos.
library(np)
data("cps71")
par(mfrow = c(1,1), mar = c(4, 4, 1, 1))
plot(logwage ~ age, data = cps71, col = "blue", pch=19, cex = 0.8,
xlab = "Idade", ylab = "Salário anual em 1971 (escala logaritmica)"); grid()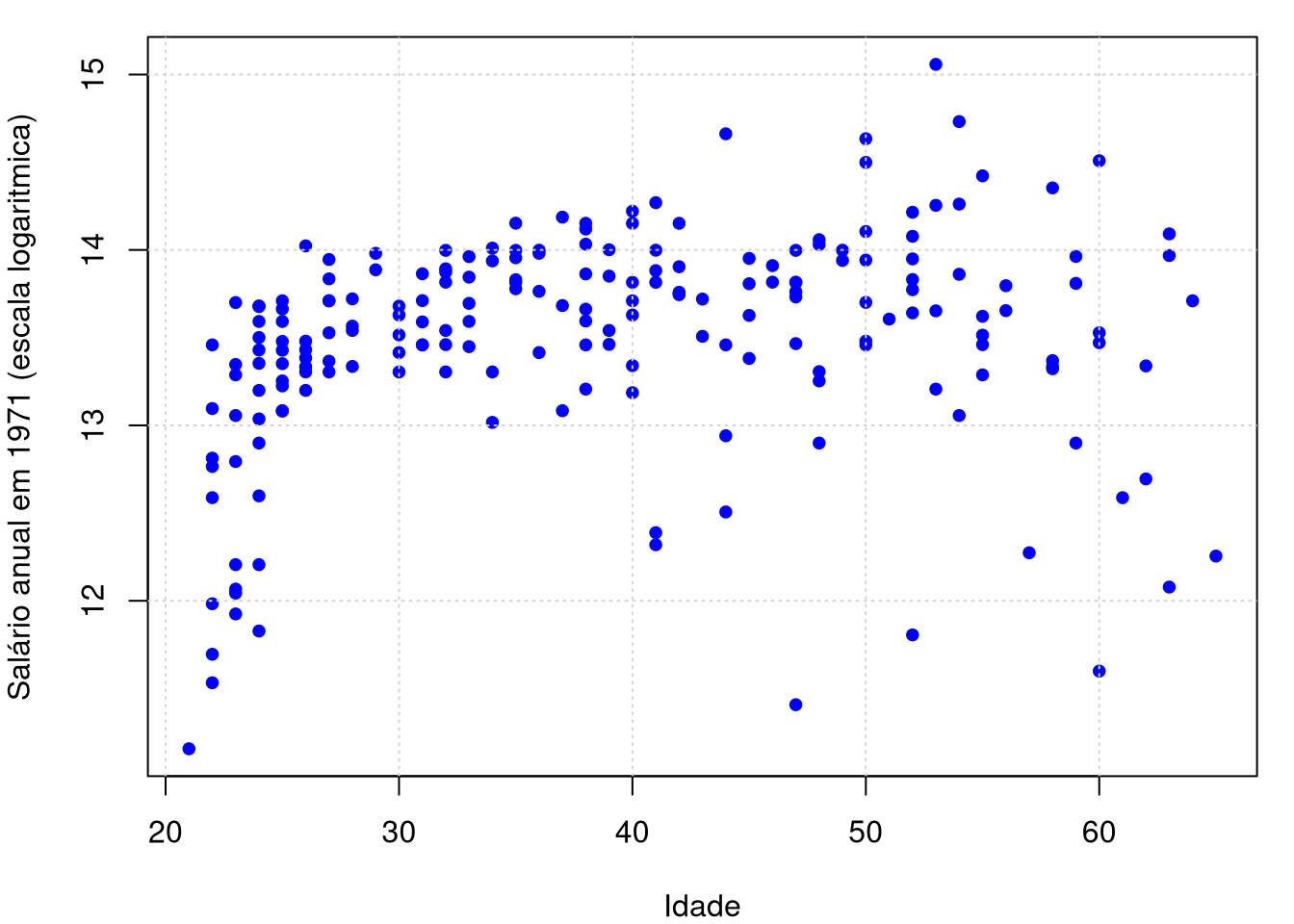
##
## Call:
## lm(formula = logwage ~ age + I(age^2), data = cps71)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.4041 -0.1711 0.0884 0.3182 1.3940
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.0419773 0.4559986 22.022 < 2e-16 ***
## age 0.1731310 0.0238317 7.265 7.96e-12 ***
## I(age^2) -0.0019771 0.0002898 -6.822 1.02e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5608 on 202 degrees of freedom
## Multiple R-squared: 0.2308, Adjusted R-squared: 0.2232
## F-statistic: 30.3 on 2 and 202 DF, p-value: 3.103e-12par(mfrow = c(1,1), mar = c(4, 4, 1, 1))
plot(logwage ~ age, data = cps71, col = "blue", pch=19, cex = 0.8,
xlab = "Idade", ylab = "Salário anual em 1971 (escala logaritmica)"); grid()
lines(cps71$age, fitted.values(model.par), col="darkblue", lwd = 3)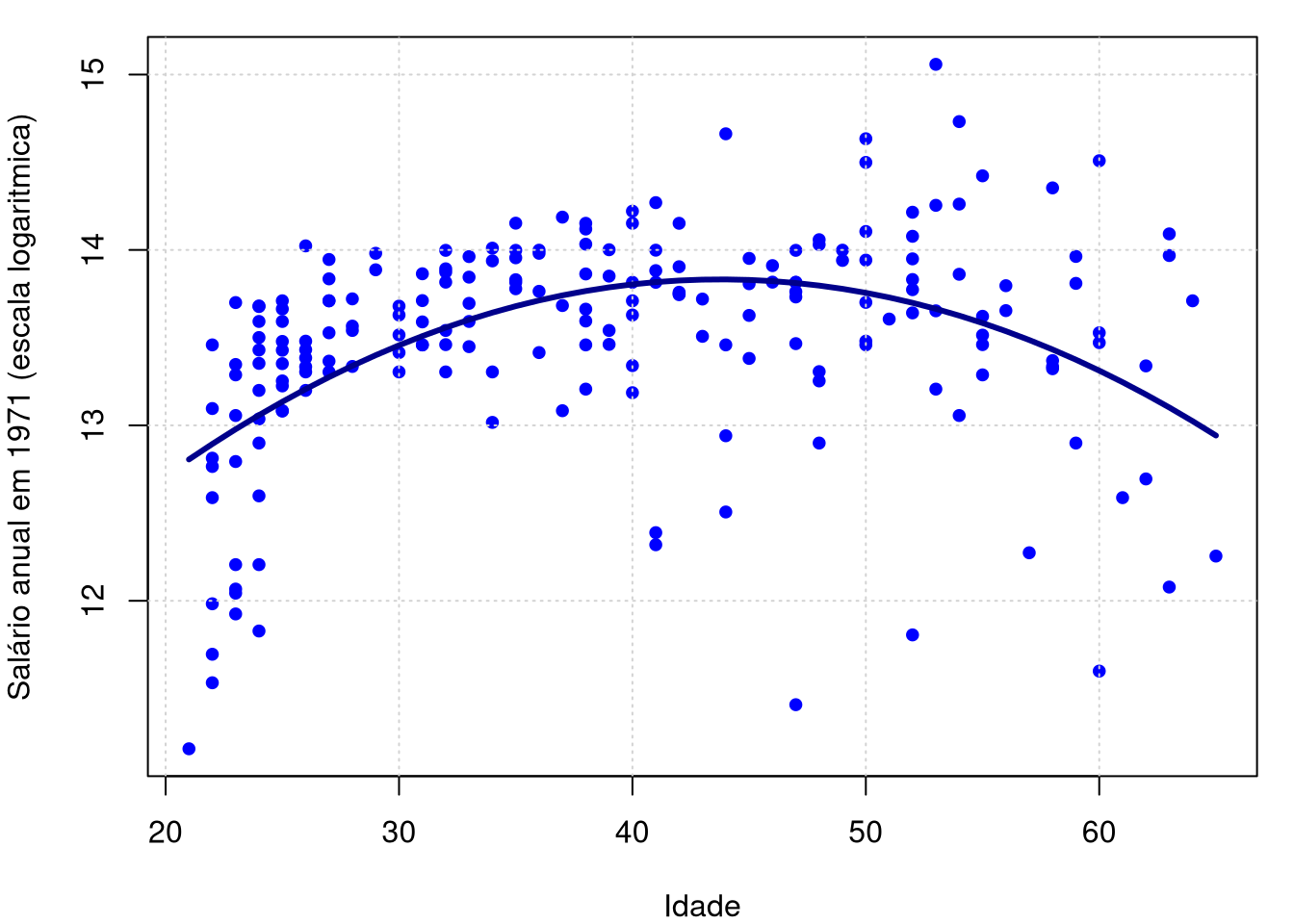
Estas figuras mostram a descrição dos dados acima e depois o modelo de regressão paramétrico estimado.
Nós temos medições ruidosas de \(Y_i\) e \(r(x_i)=10.0419+0.1731age-0.0019age^2\). Nosso objetivo é estimar \(r\) de forma não paramétrica. A variância \(\mbox{Var}(\epsilon_i)\) definitivamente não é constante como uma função de \(x\).
Os métodos que consideramos aqui são os métodos de regressão local e métodos de penalização. O primeiro inclui a regressão kernel e a regressão polinomial local. Este último leva a métodos baseados em splines. Todos os estimadores considerados são suavizadores lineares.
Antes de mergulharmos na regressão não-paramétrica, primeiro revisamos brevemente a regressão linear ordinária e sua regressão logística relativa próxima.
1.1 Regressão linear - revisão
Suponhamos temos os dados \((x_1,Y_1),\cdots,(x_n,Y_n)\) onde \(Y_i\in\mathbb{R}\) e \(x_i=(x_{i1},\cdots,x_{ip})^\top\in\mathbb{R}^p\). O modelo de regressão linear assume que \[\begin{equation} Y_i \, = \, r(x_i) \, + \, \epsilon_i \, = \, \sum_{k=1}^p \beta_kx_{ik} \, + \, \epsilon_i, \qquad i=1,\cdots,n, \end{equation}\] onde \(\mbox{E}(\epsilon_i)=0\) e \(\mbox{Var}(\epsilon_i)=\sigma^2\). Normalmente, queremos incluir um intercepto no modelo, então vamos adotar a convenção de que \(x_{i1} = 1\).
A matriz de planejamento \(X\) é uma matriz de dimensão \(n\times p\) definida por \[\begin{equation} X \, = \, \begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \vdots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{np} \end{pmatrix}\cdot \end{equation}\] O conjunto \(\mathcal{L}\) de vetores que podem ser obtidos como combinações lineares das colunas de \(X\), é chamado de espaço de coluna de \(X\).
Seja \(Y_i=(Y_1,\cdots,Y_n)^\top\), \(\epsilon=(\epsilon_1,\cdots,\epsilon_n)^\top\) e \(\beta=(\beta_1,\cdots,\beta_p)^\top\). Podemos então escrever o modelo de regressão linear como \[\begin{equation} Y \, = \, X\beta \, + \, \epsilon\cdot \end{equation}\]
Os estimadores de mínimos quadrados \(\widehat{\beta}=(\widehat{\beta}_1,\cdots,\widehat{\beta}_p)^\top\) são o vetor que minimiza a soma de quadrados dos resíduos \[\begin{equation} (Y-X\beta)^\top (Y-X\beta) \, = \, \sum_{i=1}^n \left( Y_i - \sum_{k=1}^p x_{ik}\beta_k\right)^2\cdot \end{equation}\] Assumindo que \(X^\top X\) seja inversível, o estimador de mínimos quadrados é \[\begin{equation} \widehat{\beta} \, = \, (X^\top X)^{-1}X^\top Y\cdot \end{equation}\] O comando lm avalia esta expresão e, é desta forma que obtemos \(\widehat{\beta}_0=10.0419773\), \(\widehat{\beta}_1=0.1731310\) e \(\widehat{\beta}_2=-0.0019771\) com os dados do exemplo acima.
O estimador de \(r(x)\) no ponto \(x=(x_1,\cdots,x_p)^\top\) é então \[\begin{equation} \widehat{r}_n(x) \, = \, \sum_{k=1}^n \widehat{\beta}_k x_k \, = \, x^\top \widehat{\beta}\cdot \end{equation}\] Avaliando esta equação obtemos a curva estimada do logaritmo da renda anual segunda a idade do declarante, isto realizado com o auxílio do comando fitted.values aplicado no objeto model.par.
Segue-se que os valores ajustados \(\widehat{r}_n(x)=(\widehat{r}_n(x_1),\cdots,\widehat{r}_n(x_n))^\top\) podem ser escritos matricialmente como \[\begin{equation} \widehat{r}_n(x) \, = \, X\widehat{\beta} \, = \, HY, \end{equation}\] onde \[\begin{equation} H \, = \, X(X^\top X)^{-1}X^\top \end{equation}\] é chamada de matriz hapêu. Os elementos do vetor \(\widehat{\epsilon} = Y − \widehat{r}_n(x)\) são chamados de resíduos ordinários.
A matriz chapêu é simétrica \(H = H^\top\) e idempotente, \(H^2 = H\). Segue-se que \(\widehat{r}_n(x)\) é a projeção de \(Y\) no espaço de colunas \(\mathcal{L}\) de \(X\). Pode-se mostrar que o número de parâmetros \(p\) está relacionado à matriz \(H\) pela equação \[\begin{equation} p \, = \, \mbox{tr}(H) \end{equation}\] onde \(\mbox{tr}(H)\) denota o traço da matriz \(H\), isto é, a soma dos seus elementos na diagonal principal. Na regressão não paramétrica, o número de parâmetros será substituído pelos graus de liberdade efetivos que serão definidos através de uma equação como \(p \, = \, \mbox{tr}(H)\).
Dado qualquer \(x=(x_1,\cdots,x_p)^\top\), podemos escrever \[\begin{equation} \widehat{r}_n(x) \, = \, \mathcal{l}(x)^\top Y \, = \, \sum_{i=1}^n \mathcal{l}_i(x)Y_i, \end{equation}\] sendo que \[\begin{equation} \mathcal{l}(x)^\top \, = \, x^\top(X^\top X)^{-1}X^\top\cdot \end{equation}\]
Um estimador não viciado de \(\sigma^2\) é \[\begin{equation} \widehat{\sigma}^2 \, = \, \dfrac{1}{n-p}\sum_{i=1}^n\big( Y_i-\widehat{r}_n(x_i)\big)^2 \, = \, \dfrac{||\widehat{\epsilon}||}{n-p}\cdot \end{equation}\] Em seguida, construímos uma banda de confiança para \(\widehat{r}_n(x)\). Queremos encontrar um par de funções \(a(x)\) e \(b(x)\) tais que \[\begin{equation} P\Big( \big\{x\in\mathbb{R}^p \, : \, a(x)\leq \widehat{r}_n(x)\leq b(x), \, \forall \, x \big\}\Big) \geq 1-\alpha\cdot \end{equation}\]
Dado que \(\widehat{r}_n(x) \, = \, \sum_{i=1}^n \mathcal{l}_i(x)Y_i\), segue que \[\begin{equation} \mbox{Var}\big(\widehat{r}_n(x) \big) \, = \, \sigma^2 \sum_{i=1}^n \mathcal{l}_i^2(x) \, = \, \sigma^2||\mathcal{l}||^2, \end{equation}\] o qual sugere utilizarmos bandas de confiança da forma \[\begin{equation} I(x) \, = \, \big( a(x),b(x) \big) \, = \, \Big( \widehat{r}_n(x)-c\widehat{\sigma}||\mathcal{l}(x)||, \widehat{r}_n(x)+c\widehat{\sigma}||\mathcal{l}(x)||\Big), \end{equation}\] para alguma constante \(c\). Denotemos por \(F(p, n-p)\) a variável aleatória com distribuição \(F-Fisher\) com graus de liberdade \(p\) e \(n-p\). Seja \(F_\alpha(p, n−p)\) o \(\alpha\)-quantil superior para essa variável aleatória, ou seja, \(P\big(F(p,n-p)> F_\alpha(p,n-p)\big)= \alpha\).
Teorema 1. Considere a amostra aleatória \((x_1,Y_1),\cdots,(x_n,Y_n)\) satisfazendo um modelo de regressaão linear. A banda de confiança \[\begin{equation} \Big( \widehat{r}_n(x)-\sqrt{pF_\alpha(p,n-p)}\widehat{\sigma}||\mathcal{l}(x)||, \widehat{r}_n(x)+\sqrt{pF_\alpha(p,n-p)}\widehat{\sigma}||\mathcal{l}(x)||\Big), \end{equation}\] satisfaz que \[\begin{equation} P\Big( \big\{x\in\mathbb{R}^p \, : \, {r}(x) \leq \widehat{r}_n(x)\pm \sqrt{pF_\alpha(p,n-p)}\widehat{\sigma}||\mathcal{l}(x)||, \, \forall \, x \big\}\Big) \geq 1-\alpha\cdot \end{equation}\]
Demonstração. Ver Scheffé (1959).
1.2 Regressão \(\tau_K\) de Kendall
Antes de passar para o procedimento anunciado aqui, olhamos brevemente para o modelo clássico de regressão de mínimos quadrados. Muitos leitores já estarão familiarizados com este modelo, mas enfatizamos aqui os aspectos que ajudam a entender a lógica por trás de muitas abordagens livres de distribuição.
Na abordagem paramétrica clássica, assume-se que para cada um dos \(n\) conjuntos de \(x_i\) observados, que podem ser variáveis aleatórias ou um conjunto de valores fixos que podem ou não ser escolhidos antecipadamente. Observamos algum valor \(y_i\) de uma variável aleatória \(Y_i\), que tem as propriedades que sua média depende, ou seja, é condicionada ao valor de \(x_i\) de tal forma que \[\begin{equation} \mbox{E}(Y_i|x_i) \, = \, \beta_0 + \beta_1 x_i, \end{equation}\] enquanto a variância de \(Y_i\) é independente de \(x\) e para todos os \(x_i\) tem o valor \[\begin{equation} \mbox{Var}(Y_i) \, = \, \sigma^2, \end{equation}\] onde \(\beta_0\), \(\beta_1\) e \(\sigma^2\) são desconhecidos.
A relação linear entre \(\mbox{E}(Y|x)\) e \(x\) da forma \(\mbox{E}(Y|x) = \beta_0 + \beta_1x\) entre a média condicional de \(Y\) e \(x\) dado define a regressão de \(Y\) em \(x\). A linha tem inclinação \(\beta_1\) e intercepto \(\beta_0\) no eixo \(y\). A notação \(Y_i|x_i\) é a notação convencional para um evento ou variável \(Y_i\) tendo alguma propriedade condicionada a um \(x_i\) especificado.
Para muitos fins de inferência, assume-se também que a distribuição condicional de \(Y_i | x_i\) é \(N(\beta_0 + \beta_1x_i, \sigma^2)\). Um problema clássico de regressão é estimar \(\beta_0\), \(\beta_1\) e, às vezes, também \(\sigma^2\) dado um conjunto de \(n\) observações emparelhadas \((x_1, y_1), (x_2, y_2),\cdots ,(x_n, y_n)\) onde para um dado \(x_i\) o \(y_i\) é um valor observado da variável aleatória \(Y_i\). Estas condições são válidas se cada um \((x_i, y_i)\) satisfizer \[\begin{equation} y_i \, = \, \beta_0 + \beta_1x_i + \epsilon_i, \end{equation}\] onde cada \(\epsilon_i\) é um valor não observado de uma variável aleatória \(N(0,\sigma^2)\) e os \(\epsilon_i\) são independentes uns dos outros e também de \(x_i\).
A estimativa de mínimos quadrados busca valores \(\widehat{\beta}_0\) e \(\widehat{\beta}_1\) que minimizem \[\begin{equation} S = \sum_{i=1}^n \big( y_i-\beta_0-\beta_ix_i\big)^2\cdot \end{equation}\] A linha reta \(y=\widehat{\beta}_0+\widehat{\beta}_1x\) é chamada de regressão de mínimos quadrados de \(y\) em \(x\). Se, para qualquer linha \(y=\beta_0+\beta_1x\), denotamos a coordenada \(y\) correspondente a \(x=x_i\) por \(\widehat{y}_i\), ou seja, \(\widehat{y}_i=\widehat{\beta}_0+\widehat{\beta}_1x_i\) então as diferenças entre os valores observados e previstos, isto é, \(\widehat{\epsilon}_i=y_i-\widehat{y}_i\), \(i=1,2,\cdots,n\) são chamados os resíduos absolutos com relação a essa linha.
Com os pressupostos acima da regressão clássica por mínimos quadrados é feita uma generalização de testes clássicos para comparação de médias de tratamento. Em particular, um teste de \(H_0: \, \beta_1=0\) equivale a um teste de igualdade de um conjunto de médias. Isso decorre de considerarmos os \(x_i\) como indicadores ou rótulos anexados às amostras. Se houver \(n\) observações emparelhadas \((x_i, y_i)\), cada \(y_i\) correspondente a um \(x_i\) particular pode ser encarado como um valor observado a partir da amostra marcada por esse \(x_i\). O número total de amostras \(m\) pode ser qualquer número entre 2 e \(n\) e o número de observações \(n_j\), na amostra \(j\), \(j = 1, 2,\cdots, m\) estão sujeitos à restrição \(n_1 + n_2 +\cdots + n_m = n\).
Em particular, se não houver dois \(x_i\) iguais, existem \(n\) amostras, cada uma de uma observação e, no outro extremo, se houver apenas duas \(x_i\) distintas, há duas amostras com número de observações \(n_1\) e \(n_2 = n-n_1\), respectivamente. Suponha que neste último caso marcamos a primeira amostra por \(x = 0\) e a segunda categoria por \(x = 1\) e os primeiros valores de amostra são \[\begin{equation} y_{11}, y_{12}, \cdots,y_{1n_1} \end{equation}\] com média \(\mu_0\) e os valores da segunda amostra sejam \[\begin{equation} y_{21}, y_{22}, \cdots,y_{2n_2} \end{equation}\] com média \(\mu_1\).
Pode então ser mostrado que \(\widehat{\beta}_1 = \mu_1 - \mu_0\), a diferença de média amostral utilizada no teste \(t\) para a igualdade das médias dos tratamentos. Assim, o teste de igualdade de médias é, neste caso, idêntico ao teste \(H_0 \, : \, \beta_1 = 0\). No caso mais geral de \(m\) amostras, um teste para \(\beta_1 = 0\) é um teste para a identidade de todas as \(m\) médias populacionais.
É bem conhecido que para o modelo clássico de mínimos quadrados o estimador de \(\beta_1\) não depende do estimador de \(\beta_0\), mas o de \(\beta_0\) depende daquele de \(\beta_1\) através de \(\widehat{\beta}_1\), já que \(\widehat{\beta}_0 = \overline{y} - \widehat{\beta}_1\overline{x}\). A partir dessa expressão para \(\widehat{\beta}_0\) pode-se ver que a equação ajustada pode ser escrita sem referência ao intercepto na forma \[\begin{equation} y \, = \, \overline{y}-\widehat{\beta}_1(x-\overline{x}), \end{equation}\] implicando que a linha passa pelo ponto \((\overline{x},\overline{y})\).
Uma interpretação gráfica disso é que a inclinação da linha ajustada é inalterada por uma mudança de origem. Em particular, se mudarmos a origem para a média bivariada \((\overline{x},\overline{y})\) e escrevermos \(\widetilde{x}= x - \overline{x}\), \(\widetilde{y} = y - \overline{y}\) a equação acima se torna \[\begin{equation} \widetilde{y} \, = \, \widehat{\beta}_1 \widetilde{x} \end{equation}\] e, então \[\begin{equation} \widehat{\beta}_1 \, = \, \frac{\displaystyle\sum_{1=1}^n \widetilde{x}_i\widetilde{y}_i}{\displaystyle\sum_{i=1}^n \widetilde{x}_i^2}\cdot \end{equation}\]
A expressão acima ainda é válida se apenas mudarmos a origem para a média dos \(x_i\) e usarmos o \(y_i\) original. Foi apontado que o coeficiente de correlação de Pearson permanece inalterado por transformações lineares de \((x, y)\) da forma \(x'= (x - k)/s\) e \(y' = (y - m)/t\) onde \(s\), \(t\) ambos são positivos. Acabamos de ver que, em regressão, embora a estimativa de \(\beta_0\) seja afetada por uma mudança na origem, a de \(\beta_1\) não é, isto é, transformações da forma \(x'= (x - k)\), \(y' = (y - m)\) não afetam a estimativa de \(\beta_1\). Entretanto, pode-se estabelecer que a transformação \(x'= (x - k)/s\) e \(y' = (y - m)/t\) altera tanto o valor verdadeiro de \(\beta_1\) quanto sua estimativa de mínimos quadrados pelo mesmo fator de escala \(s/t\), alterando \(\beta_1\) para \(\beta_1'= s\beta_1/t\).
No entanto, faremos uso de outra propriedade do coeficiente de correlação de Pearson em testes permutacionais, ou seja, porque todas as outras quantidades na expressão da estimativa do coeficiente de correlação de Pearson permanecem constantes sob permutações, podemos basear testes de permutação na estatística \(T = \sum_i x_iy_i\) no caso do coeficiente de Pearson como alternativa ao uso do coeficiente de correlação amostral \(r\). Uma propriedade correspondente é transferida para o coeficiente de Spearman com postos substituindo os \(x_i\), \(y_i\).
Descartando a suposição de normalidade para o \(Y_i\), fazer inferências sobre \(\beta_0\) e \(\beta_1\) são difíceis, então consideramos primeiro a estimação apenas de \(\beta_1\). O problema reduz-se então a fazer inferências sobre diferenças em medianas ou médias amostrais marcadas pelos diferentes \(x_i\). Para qualquer \(Y_i,Y_j\) independentes, associados com \(x_i,x_j\) distintos, descartamos as suposções de normalidade nas distribuições condicionais de \(Y | x\) e assumimos agora apenas que para qualquer \(x_i, x_j\) elas têm distribuições \(F_i (Y_i | x_i)\), \(F_j (Y_j | x_j)\) que diferem apenas na sua medida de centralidade que será assumida, em geral, como a mediana, mas que coincidirá com a média das distribuições condicionais que são assumidas simétricas, desde que a média exista.
Para o modelo de regressão linear, a mediana de \(F_i(Y_i|x_i)\) é \(\mbox{Mediana}(Y_i|x_i)=\beta_0+\beta_1 x_i\) e aquela de \(F_j(Y_j|x_j)\) é \(\mbox{Mediana}(Y_j|x_j)=\beta_0+\beta_1 x_j\), sendo estes os análogos da estimativa do coeficiente de correlação e a diferença entre as medianas é claramente \[\begin{equation} \mbox{Mediana}(Y_j-Y_i|x_i,x_j)=\beta_1 (x_j-x_i)\cdot \end{equation}\]
Assumindo que as diferenças entre as distribuições estão confinadas a uma diferença mediana implica que, para todo \(i\) \[\begin{equation} D_i(\beta_1) = Y_i-\beta_1x_i, \end{equation}\] são distribuídas de forma idêntica e independente com mediana \(\beta_0\). Como os \(D_i\) são, portanto, independentes do \(x_i\), segue-se que eles não são correlacionados com o \(x_i\). Como apontamos, o \(x_i\) pode ser alterado pela adição ou subtração de uma constante sem afetar a inclinação ou sua estimativa. Em particular, ele simplificará a àlgebra se ajustarmos o \(x_i\) adicionando uma constante apropriada para fazer \(\sum_i x_i = 0\), o que, em termos gráficos, implica mudar a origem para um ponto no eixo \(x\) correspondente à média \(\overline{x}\).
Escrevendo \(\widehat{D}_i = y_i - \beta x_i\) um teste intuitivamente razoável da hipótese \(H_0 \, : \, \beta_1 = \beta\) contra uma alternativa de um ou dois lados é um teste para a correlação zero entre o \(x_i\) e o \(\widehat{D}_i\), pois sabemos que se \(H_0\) é válido então \(D_i(\beta)\) não é correlacionado com o \(x_i\) e os \(\widehat{D}_i\) são valores observados da variável \(D_i(\beta)\). Se o teste mais apropriado é baseado em Pearson, Spearman, Kendall ou algum outro coeficiente dependerá de quais suposições sejam feitas sobre as características da distribuição \(F(Y|x)\), por exemplo, cauda longa, simétrica ou assimétrica, etc.. Nós chamamos os \(\widehat{D}_i\) de resíduos por conveniência, mas este é um uso não ortodoxo do termo que mais convencionalmente se refere ao \(\widehat{\epsilon}_i = y_i - \alpha - \beta x_i\) onde \(\alpha\) é algum valor hipotético de \(\beta_0\). Uma estatística apropriada baseada no coeficiente de Pearson para o teste de correlação zero é \[\begin{equation} T(\beta) \, = \, \sum_{i=1}^n x_i\widehat{D}_i \, = \, \sum_{i=1}^n x_i (y_i - \beta x_i)\cdot \end{equation}\]
Devemos lembrar que se tivermos medições em duas variáveis para uma amostra de \(n\) indivíduos, estas observações emparelhadas podem ser escritas como \((x_1, y_1), (x_2, y_2),\cdots , (x_n, y_n)\). O coeficiente de correlação amostral de produto de momentos de Pearson \(r\), é definido como \[\begin{equation} r \, = \, \frac{\sum_i\Big( (x_i-\overline{x})(y_i - \overline{y})\Big)}{\sqrt{\sum_i (x_i-\overline{x})^2\sum_i(y_i-\overline{y})^2}}\cdot \end{equation}\] que, para fins computacionais, é geralmente reordenada e escrita como \[\begin{equation} r \, = \, \frac{C_{xy}}{\sqrt{C_{xx}C_{yy}}}, \end{equation}\] sendo \[\begin{equation} C_{xy}=\sum_i x_iy_i-(\sum_i x_i)(\sum_i y_i)/n, \qquad C_{xx}=\sum_i x_i^2-(\sum_i x_i)^2/n \end{equation}\] e \[\begin{equation} C_{yy}=\sum_i y_i^2-(\sum_i y_i)^2/n\cdot \end{equation}\]
Voltando ao nosso desenvolvimento. Observemos que, para estimar \(\beta\), um procedimento de estimação intuitivamente razoável é resolver para \(\beta\) a equação \[\begin{equation} T(\beta) \, - \, \sum_{i=1}^n x_i \sum_{i=1}^n \widehat{D}_i/n \, = \, 0\cdot \end{equation}\] Isso segue da forma de \(C_{xy}\), já que equalizar \(C_{xy}\) a zero garante um valor zero para o coeficiente de correlação amostral, uma vez que torna o numerador do coeficiente de correlação amostral de Pearson zero. Lembrando que podemos ajustar o \(x_i\) para ter a média zero, ou seja, de modo que \(\sum_i x_i = 0\) sem afetar nossa estimativa de \(\beta\), assumimos que isso foi feito para que a equação acima simplifique para \[\begin{equation} T(\beta) \, = \, \sum_{i=1}^n x_i( y_i - \beta x_i) \, = \, 0, \end{equation}\] com solução \(\widehat{\beta}=(\sum_i x_i y_i)/(\sum_i x_i^2)\).
Não fizemos suposições sobre a distribuição do \(D_i\) exceto que eles são idênticos para todos os \(i\), de modo que, para o teste de hipótese, um teste de permutação para o coeficiente de correlação de Pearson ser zero com base nos valores amostrais \((x_i, \widehat{D}_i)\) é apropriado. Como indicamos em outros casos, uma dificuldade com inferências baseadas em dados brutos usando um teste de permutação é que os resultados tendem a ser similares àqueles baseados na teoria equivalente, assumindo normalidade mesmo quando a suposição de normalidade seja claramente violada. Em outras palavras, o método não tem robustez. Melhores procedimentos para lidar com dados são geralmente fornecidos por procedimentos de estimação baseados em classificaçao.
Vejamos como fazer inferências baseadas no coeficiente \(\tau_K\) de Kendall. Sabemos que \(\tau_K\) depende apenas da ordem das observações e não da magnitude das diferenças entre os valores dos dados. Além disso, não há vantagem em ajustar o \(x_i\) para terem média zero. Simplifica a apresentação sem perda de generalidade se, quando os \(x_i\) são todos diferentes, assumimos que \(x_1 < x_2 \cdots < x_n\).
A estatística usada para inferência sobre \(\beta\) é \[\begin{equation} T_t(\beta) \, = \, \sum_i \mbox{sgn}\big( \widehat{D}_{ij}(\beta)\big), \end{equation}\] onde \[\begin{equation} \begin{array}{rcl} \widehat{D}_{ij}(\beta) & = & (y_j - \widehat{\beta}_0 - \widehat{\beta} x_j) - (y_i - \widehat{\beta}_0 - \widehat{\beta} x_i) \, = \, (y_j - \widehat{\beta} x_j) - (y_i - \widehat{\beta} x_i) \\ & = & \widehat{D}_{j} - \widehat{D}_{i} \, = \, (y_j - y_i) - \widehat{\beta}(x_j - x_i) \end{array} \end{equation}\] e e soma dos sinais dos \(\widehat{D}_{ij}\) é sobre todo \(i=1,2,\cdots,n-1\) e \(j> i\). Como os \(x_i\) são todos diferentes e em ordem ascendente é claro que \(T_t(\beta)\) é o numerador na expressão da estatística de teste para verificar nulidade do coeficiente \(\tau_K\) composto dos números de concordâncias menos o número de discordâncias nos pares de dados \((x_i,\widehat{D}_i)\).
O uso de uma estatística equivalente a \(T_t(\beta)\) foi proposto pela primeira vez por Theil (1950) e o procedimento é amplamente conhecido como o método de Theil. Sen (1968) destacou a relação com o coeficiente \(\tau_K\) de Kendall, então nos referimos a ele como o método Theil-Kendall ou estimador Theil-Sen.
Claramente \(T_t(\beta)\) é uma função linear do estimador amostral de \(\tau_K\) e um estimador de pontual apropriado de \(\beta\) é obtido ajustando-se \(T_t(\beta) = 0\). Como os \(x_i\) estão em ordem ascendente podemos observar que \(T_t(\beta)\) não é alterada se substituirmos \(\widehat{D}_{ij}(\beta)\) por \(\widehat{B}_{ij} - \beta\) onde, \[\begin{equation} \widehat{B}_{ij} = (y_j - y_i)/(x_j - x_i)\cdot \end{equation}\] Claramente, então, \(T_t(\beta) = 0\), se escolhermos \(\beta = \mbox{Mediana}(\widehat{B}_{ij})\), então o número de positivos e o número de \(\widehat{D}_{ij}\) negativos serão iguais.
Como foi o caso de \(T_s(\beta)\), percebemos que apenas \(T_t(\beta)\) muda de valor quando \(\beta\) passa por um valor de \(\widehat{B}_{ij}\) e como a estatística é o numerador do coeficiente \(\tau_K\) de Kendall, segue-se que se todos os \(\widehat{B}_{ij}\) são distintos quando \(\beta\) aumenta de \(-\infty\) para \(\infty\), \(T_t(\beta)\) é uma função degrau decrescente por passos de 2 desde ½\(n(n-1)\) para -½\(n(n - 1)\).
Claramente a divisão de \(T_t(\beta)\) por ½\(n(n-1)\) leva ao \(t_K\) de Kendall, que pode ser usado como uma estatística equivalente. Se os \(\widehat{D}_{ij}\) não forem todos distintos, alguns dos passos serão múltiplos de 2. Em particular, se um \(\widehat{D}_{ij}\) ocorre \(r\) vezes, ele induz um degrau de altura \(2r\). O valor de \(T_t(\beta)\) em qualquer \(\widehat{D}_{ij}\) pode ser considerado como a média dos valores imediatamente acima e abaixo daquele \(\widehat{D}_{ij}\).
Testes de hipóteses sobre \(\beta\) são diretos usando ou o \(t_K\) de Kendall ou o equivalente \(T_t(\beta)\) como estatística de teste e se sabemos a distribuição exata do coeficiente de Kendall amostral quando \(\tau_K = 0\), um intervalo de confiança para \(\beta\) pode ser obtido. Os procedimentos estão ilustrados no Exemplo a seguir.
Exemplo 2.
O fluxo de água em metros cúbicos por segundo \(y\), em um ponto fixo de um córrego da montanha é registrado em intervalos de uma hora \(x\) após um degelo de neve, começando no tempo \(x = 0\).
Sendo que \(horas\) são as horas a partir do início do degelo e \(fluxo\) registra o fluxo de água em metros cúbicos/seg. Durante os degelos anteriores, tem havido frequentemente uma relação quase linear entre o tempo e o fluxo. Use o método de Theil-Kendall para:- testar a hipótese \(H_0 : \beta_1 = 1\) contra a alternativa \(H_1: \beta_1\neq 1\);
- obter uma estimativa pontual de \(\beta_1\) e um intervalo de confiança que dê pelo menos 95 por cento de cobertura.
Primeiro vamos ajustar o modelo de regressão de Theil-Kendall ou Theil-Sen, para isso utilizamos a função mblm no pacote homônimo.
library(mblm)
ajuste0 = mblm(fluxo ~ horas, repeated = FALSE)
ajuste1 = lm(fluxo ~ horas)
summary(ajuste0)##
## Call:
## mblm(formula = fluxo ~ horas, repeated = FALSE)
##
## Residuals:
## 1 2 3 4 5 6 7
## 0.16667 0.20000 -0.06667 -0.03333 0.00000 -0.06667 5.36667
##
## Coefficients:
## Estimate MAD V value Pr(>|V|)
## (Intercept) 2.33333 0.09884 28 0.0156 *
## horas 0.56667 0.09884 231 6.39e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.403 on 5 degrees of freedompar(mfrow = c(1,1), mar = c(4, 5, 2, 1), pch = 19)
plot(fluxo ~ horas, pch = 19, xlab = "Horas a partir do início do degelo",
ylab = "Fluxo em metros cúbicos/seg"); grid()
abline(ajuste0, lty = 1, lwd = 2, col = "red")
text(4.5,4, "Modelo Theil–Kendall", col = "red")
abline(ajuste1, lty = 1, lwd = 2, col = "blue")
text(4,8, "Modelo de regressão linear", col = "blue")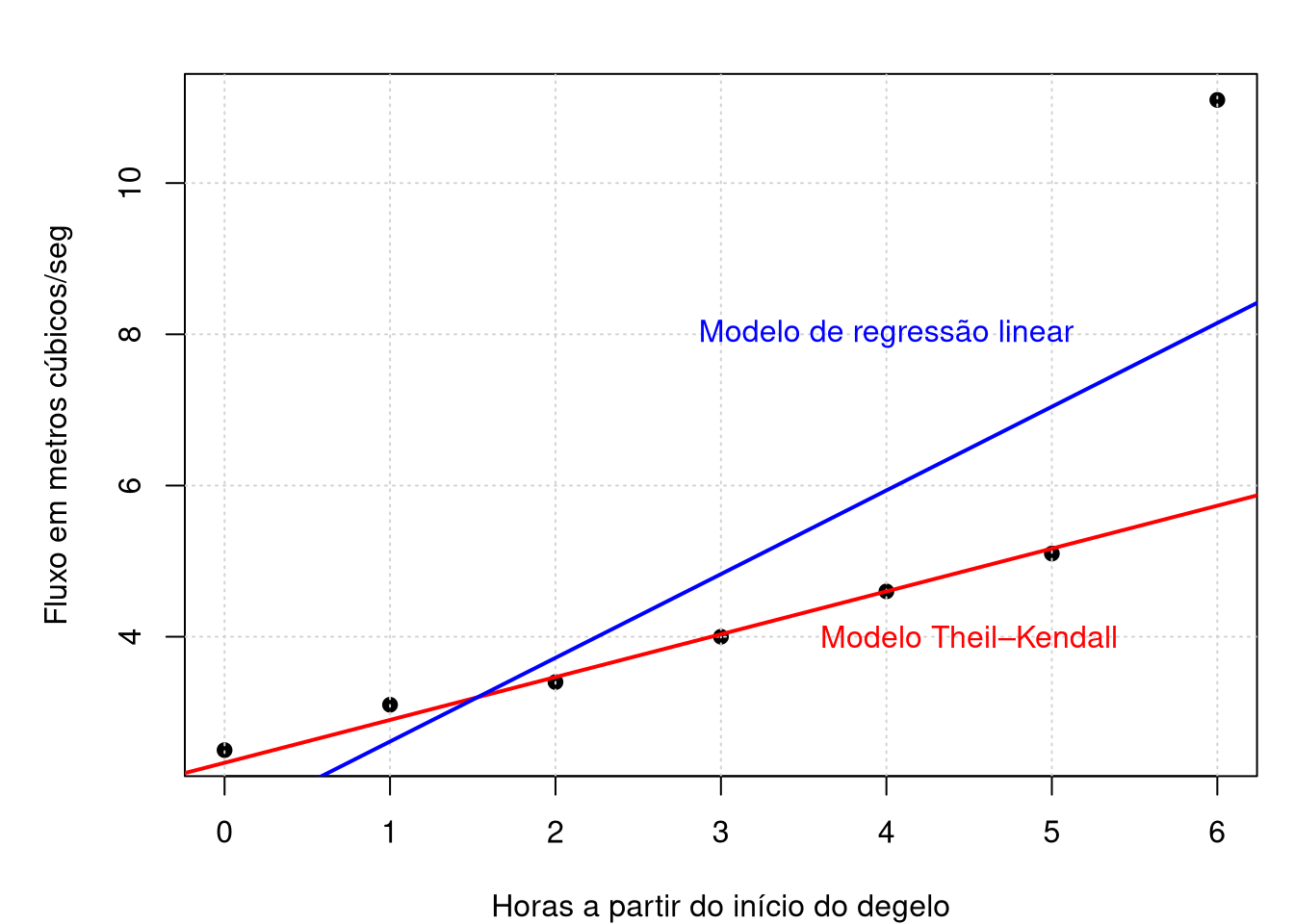
No gráfico acima mostramos o comportamento do modelo de regressão linear assim como do modelo não paramémetrico de Theil-Kendall ou Theil-Sen.
A regressão de Kendall-Theil é uma abordagem completamente não-paramétrica à regressão linear, onde existe uma variável independente e uma variável dependente. É robusto para outliers na variável dependente, como podemos perceber. Ele simplesmente calcula todas as linhas entre cada par de pontos e usa a mediana das inclinações dessas linhas. O método produz um declive e um intercepto para a linha de ajuste, assim como um \(p\)-valor para a inclinação também pode ser determinado.
Normalmente, nenhuma medida análoga ao \(R^2\) é relatada. Na Seção IV.2.1 Avaliando a qualidade do ajuste, estudaremos uma forma alternativa de escrever \(R^2\) que poderemos utilizar nesta situação.
Para testar a hipótese em i, observemos que uma inspeção mostra que a estimativa pontual de \(\beta_1\), ou seja, \(\mbox{Mediana}(\widehat{B}_{ij})\) é 0.567, porque há dez maiores e dez menores \(\widehat{B}_{ij}\).
## [1] 0.6000000 0.4500000 0.5000000 0.5250000 0.5200000 1.4333333 0.3000000
## [8] 0.4500000 0.5000000 0.5000000 1.6000000 0.6000000 0.6000000 0.5666667
## [15] 1.9250000 0.6000000 0.5500000 2.3666667 0.5000000 3.2500000 6.0000000## [1] 0.5666667Para testar a hipótese \(\beta_1 = 1\) subtraímos \(\beta_1 = 1\) de cada \(\widehat{B}_{ij}\)
## [1] -0.4000000 -0.5500000 -0.5000000 -0.4750000 -0.4800000 0.4333333
## [7] -0.7000000 -0.5500000 -0.5000000 -0.5000000 0.6000000 -0.4000000
## [13] -0.4000000 -0.4333333 0.9250000 -0.4000000 -0.4500000 1.3666667
## [19] -0.5000000 2.2500000 5.0000000e encontramos que isto implica 15 discordâncias ou valores negativos e 6 concordâncias, onde \[\begin{equation} T_t(1) = 6 - 15 = –9, \end{equation}\] e quando \(n = 7\), isto implica que, \(t_K = –9/21 = 0.4286\).
## [1] 0.1361111O pacote SuppDists incorpora ao R diversas distribuições suplementares, entre elas, a distribuição exata do coeficiente de correlação \(\tau_K\) de Kendall. Utilizamos as linhas de comando acima para avaliarmos evidências a favor ou contra \(H_0\). Correspondendo a este valor de \(t_K\) com \(N=7\), os sete pares de dados, o \(p\)-valor = 0.1361111 é exatamente bilateral de modo que não há evidência convincente contra \(H_0\).
Para obter um intervalo de confiança aproximado de 95 por cento para \(\beta_1\), devemos primeiro determinar um valor de \(|T_t|\) com cauda o mais próxima possível, mas não superior a 0.025.
## [1] -13## [1] 13Para obter um intervalo de confiança aproximado de 95 por cento para \(\beta_1\), devemos primeiro determinar um valor de \(|T_t|\) com uma cauda o mais próximo possível, mas não superior a 0.025. A distribuição exata quando \(n = 7\) dado pelo R indica que para probabilidade na cauda de 0.025, \(T_t = 13\). Obtemos o intervalo
## [1] 0.6190476## [1] 0.5542825## [1] 1.792378ou (0.5542825,1.792378).
A estreita relação entre o \(\tau_K\) de Kendall e o \(T_t\) facilita o transporte de aproximações assintóticas entre eles. Usando os resultados para \(\tau_K\) pode-se mostrar (Maritz, 1995) que
\[\begin{equation}
\mbox{E}(T_t) = 0 \qquad \mbox{ e que } \qquad \mbox{Var}(T_t) = \frac{n (n - 1) (2n + 5)}{18}\cdot
\end{equation}\]
Para grandes \(n\) a distribuição de \(Z = T_t / \sqrt{\mbox{Var}(T_t)}\) é aproximadamente normal e inferências assintóticas podem então ser feitas da maneira usual. Mesmo para \(n = 7\), a aproximação às vezes não é seriamente enganosa, mas recomenda-se cautela com uma amostra tão pequena.
A regressão de Kendall-Theil também chamada de regressão de Theil-Sen é uma robusta substituição não-paramétrica da abordagem tradicional de mínimos quadrados ao modelo de regressão de linha reta \(Y = \beta_0 + \beta_1x + \epsilon\) e também a alguns modelos de regressão linear mais complexos. Esta metodologia não exige normalidade dos erros aleatórios, sendo capaz de fornecer estimativas dos parâmetros, testes de hipóteses lineares sobre os parâmetros, bem como intervalos de confiança para os parâmetros. Ver, por exemplo, Hollander, M. et. all. (2014) para uma descrição mais detalhada do método.