Capítulo 2 Suavizamento linear
Como observamos, os estimadores não-paramétricos aqui considerados são suavizadores lineares. A definição formal é mostrada a seguir.
Definição 1. Um estimador \(\widehat{r}_n\) de \(r\) é dito ser um suavizador linear se, para cada \(x\), existe um vetor \(\mathcal{l}(x)=(\mathcal{l}_1(x),\cdots,\mathcal{l}_n(x))^\top\) tal que \[\begin{equation} \widehat{r}_n(x) \, = \, \sum_{i=1}^n \mathcal{l}_i(x)Y_i\cdot \end{equation}\]
Definindo o vetor de valores ajustados \[\begin{equation} \widehat{r}_n(x) \, = \, \big( \widehat{r}_n(x_1),\cdots,\widehat{r}_n(x_n)\big)^\top, \end{equation}\] segue-se então que \[\begin{equation} \widehat{r}_n(x) \, = \, LY, \end{equation}\] onde \(L\) é uma matriz \(n\times n\) cuja \(i\)-ésima linha é \(\mathcal{l}_i(x)^\top\), assim, \(L_{ij} = \mathcal{l}_j(x_i)\). As entradas da \(i\)-ésima linha mostram os pesos dados a cada \(Y_i\) na formação da estimativa \(\widehat{r}_n(x_i)\).
Definição 2. A matriz \(L\) é chamada matriz de suavização. A \(i\)-ésima linha de \(L\) chama-se kernel efetivo para estimar \(r(x_i)\). Definimos os graus de liberdade efetivos como \[\begin{equation} \nu \, = \, \mbox{tr}(L)\cdot \end{equation}\]
O leitor não deve confundir suavizadores lineares com regressão linear, em que se assume que a função de regressão \(r(x)\) é linear. Devemos observar que os pesos em todos os suavizadores que usaremos terão a propriedade que, para todo \(x\), \(\sum_{i=1}^n \mathcal{l}_i(x) = 1\). Isto implica que o suavizador preserva curvas constantes, portanto, se \(Y_i = c\) para todo \(i\), então \(\widehat{r}_n(x) = c\).
Exemplo 3. (Regressograma)
Suponhamos \(x\) limitado, mas claramente, vamos asumir que \(a\leq x_i\leq b\) \(\forall i\). Vamos dividir o intervalo \((a,b)\) em \(m\) caixas igualmente espaçadas denotadas por \(B_1,B_2,\cdots,B_m\). Definamos \(\widehat{r}_n(x)\) por \[\begin{equation} \widehat{r}_n(x) \, = \, \frac{1}{n_j} \sum_{\{ \, i \, : \, x\in B_i \, \}}Y_i, \qquad \forall x\in B_j, \end{equation}\] sendo \(n_j\) o número de pontos em \(B_j\). Em outras palavras, a estimativa de \(\widehat{r}_n\) é uma função de passo obtida pela média do \(Y_i\) sobre cada caixa. Essa estimativa é chamada de regressograma.
Um exemplo de regressograma é apresentado nas figuras abaixo. Para \(x\in B_j\) definamos \(\mathcal{l}_i(x) = 1/n_j\) se \(x_i\in B_j\) e \(\mathcal{l}_i(x)=0\) caso contrário. Assim, \(\widehat{r}_n(x)=\sum_{i=1}^n Y_i\mathcal{l}_i(x)\). O vetor de pesos \(\mathcal{l}(x)\) se parece com isso: \[\begin{equation} \mathcal{l}(x)^\top \, = \, \Big( 0,0,\cdots,0,\frac{1}{n_j},\cdots,\frac{1}{n_j},0,\cdots,0\Big)\cdot \end{equation}\] Para ver como a matriz de suavização \(L\) se parece, suponha que \(n = 9\), \(m = 3\) e \(n_1 = n_2 = n_3 = 3\). Então \[\begin{equation} L \, = \, \frac{1}{3}\times \begin{pmatrix} 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \end{pmatrix}\cdot \end{equation}\] Em geral, podemos ver existem \(\nu = \mbox{tr}(L) = m\) graus de liberdade efetivos. A largura de banda \(h=(b-a)/m\) controla a suavidade da estimativa e a matriz de alisamento \(L\) controla a forma.
Vamos utilizar os dados do Exemplo 1 com os resultados do modelo de regressão linear. Para construir as figuras abaixo fizemos alterações ao comando regressogram disponível no pacote de funções HoRM.
Como padrão a função regressogram devolve o gráfico de dispersão e a curva de regressão não paramétrica estimada pelo suavizamento linear. Como mostramos nas linhas de comando a seguir.
library(HoRM)
regressogram(cps71$age, cps71$logwage, x.lab = "age", y.lab = "logwage",
nbins = 10, main = "Regressograma", show.bins = FALSE,
show.means = FALSE, show.lines = TRUE)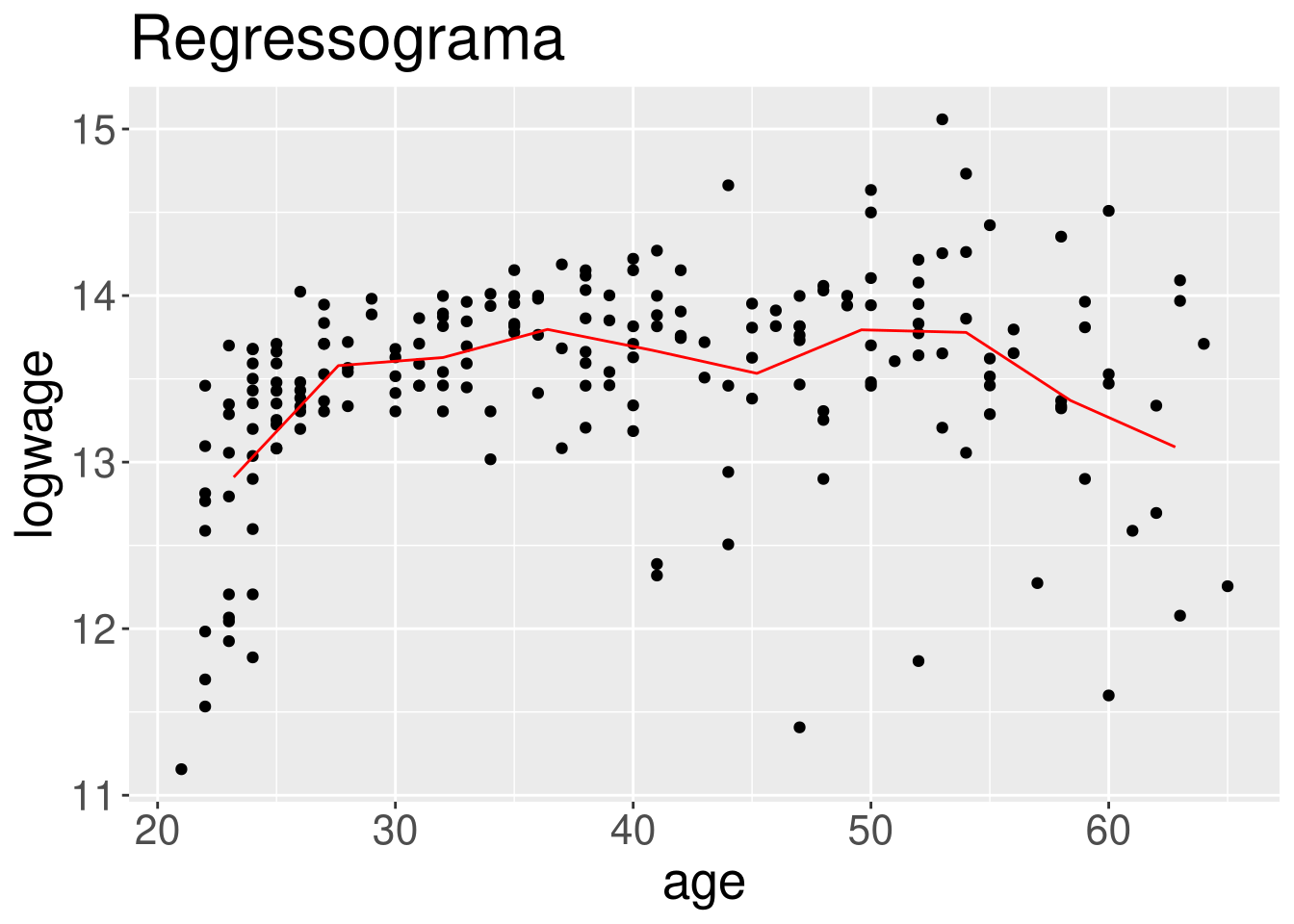
regressogram(cps71$age, cps71$logwage, x.lab = "age", y.lab = "logwage",
nbins = 20, main = "Regressograma")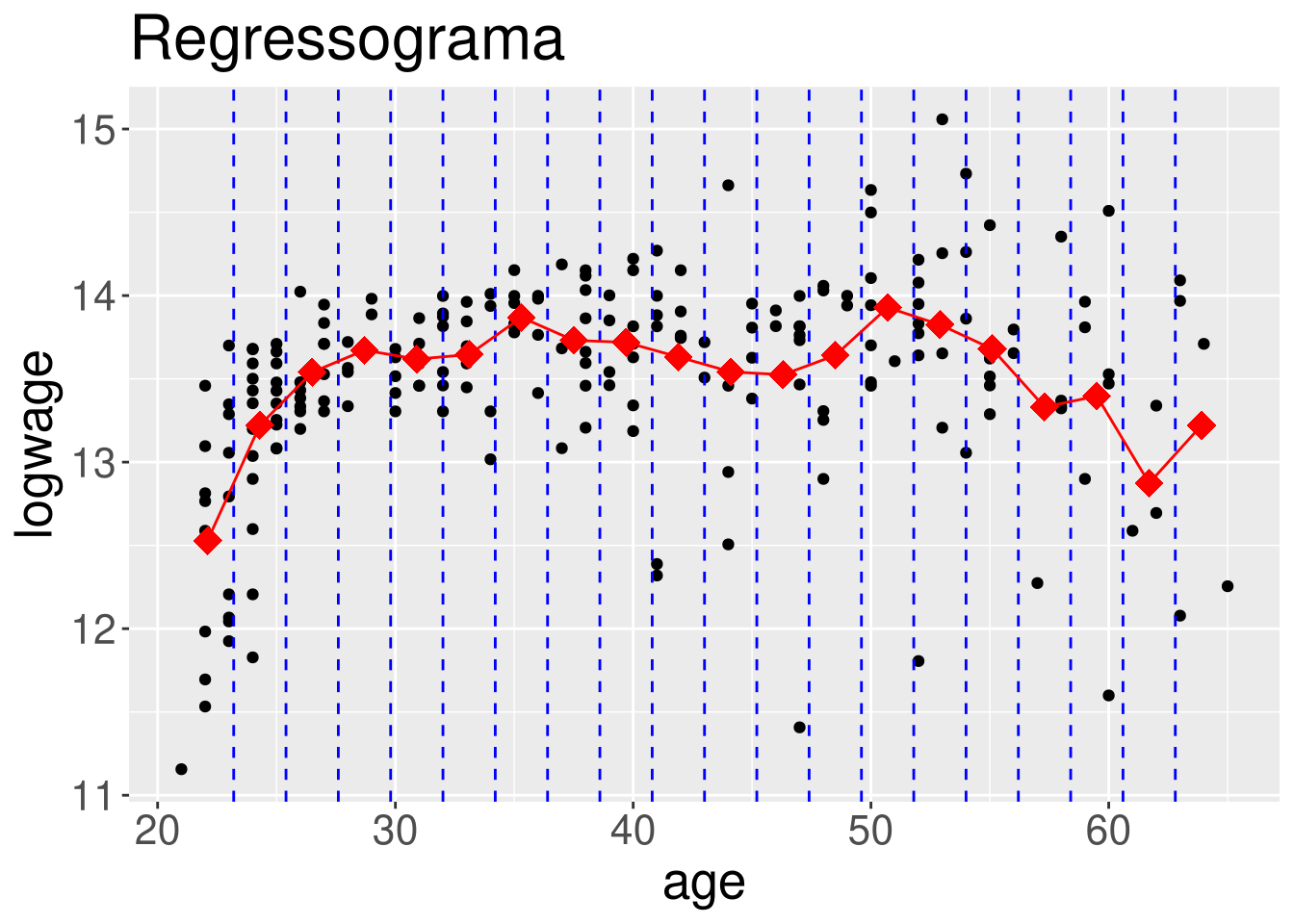
Com estes comandos obtemos duas figuras mostrando o ajuste de regressograma com \(m=10\) e \(m=20\) caixas, respectivamente. Isto foi obtido modificando o valor da opção nbins.
Um problema é que gostariamos de apresentar conjuntamente com o regressograma o ajuste do modelo de regressão paramétrico. Como isso não é possível, modificamos apropriadamente a função segundo nosso interesse, como mostramos a seguir.
regressograma = function (x, y, nbins = 10) {
xy <- data.frame(x = x, y = y)
xy <- xy[order(xy$x), ]
z <- cut(xy$x, breaks = seq(min(xy$x), max(xy$x), length = nbins +
1), labels = 1:nbins, include.lowest = TRUE)
xyz <- data.frame(xy, z = z)
MEANS <- c(by(xyz$y, xyz$z, FUN = mean))
x.seq <- seq(min(x), max(x), length = nbins + 1)
midpts <- (x.seq[-1] + x.seq[-(nbins + 1)])/2
d2 <- data.frame(midpts = midpts, MEANS = MEANS)
return(d2)
}
model.par.1 = regressograma(cps71$age, cps71$logwage, nbins = 10)
model.par.2 = regressograma(cps71$age, cps71$logwage, nbins = 20)
par(mfrow = c(1,1), mar = c(4, 4, 1, 1))
plot(logwage ~ age, data = cps71, col = "blue", pch=19)
lines(cps71$age, fitted.values(model.par), col="darkblue", lwd = 3)
lines(model.par.1$midpts, model.par.1$MEANS, col = "red", lwd = 3)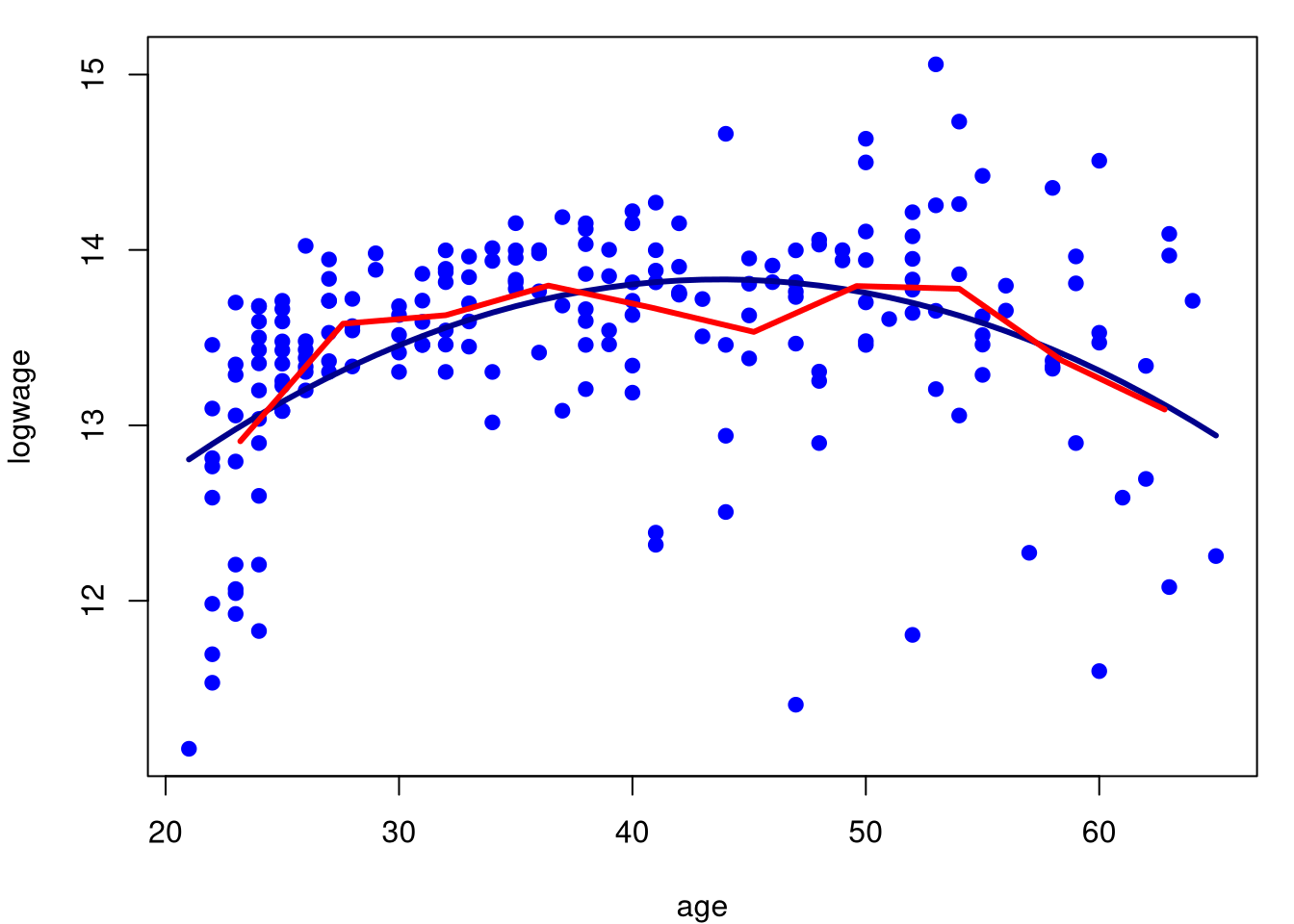
par(mfrow = c(1,1), mar = c(4, 4, 1, 1))
plot(logwage ~ age, data = cps71, col = "blue", pch=19)
lines(cps71$age, fitted.values(model.par), col="darkblue", lwd = 3)
lines(model.par.2$midpts, model.par.2$MEANS, col = "red", lwd = 3)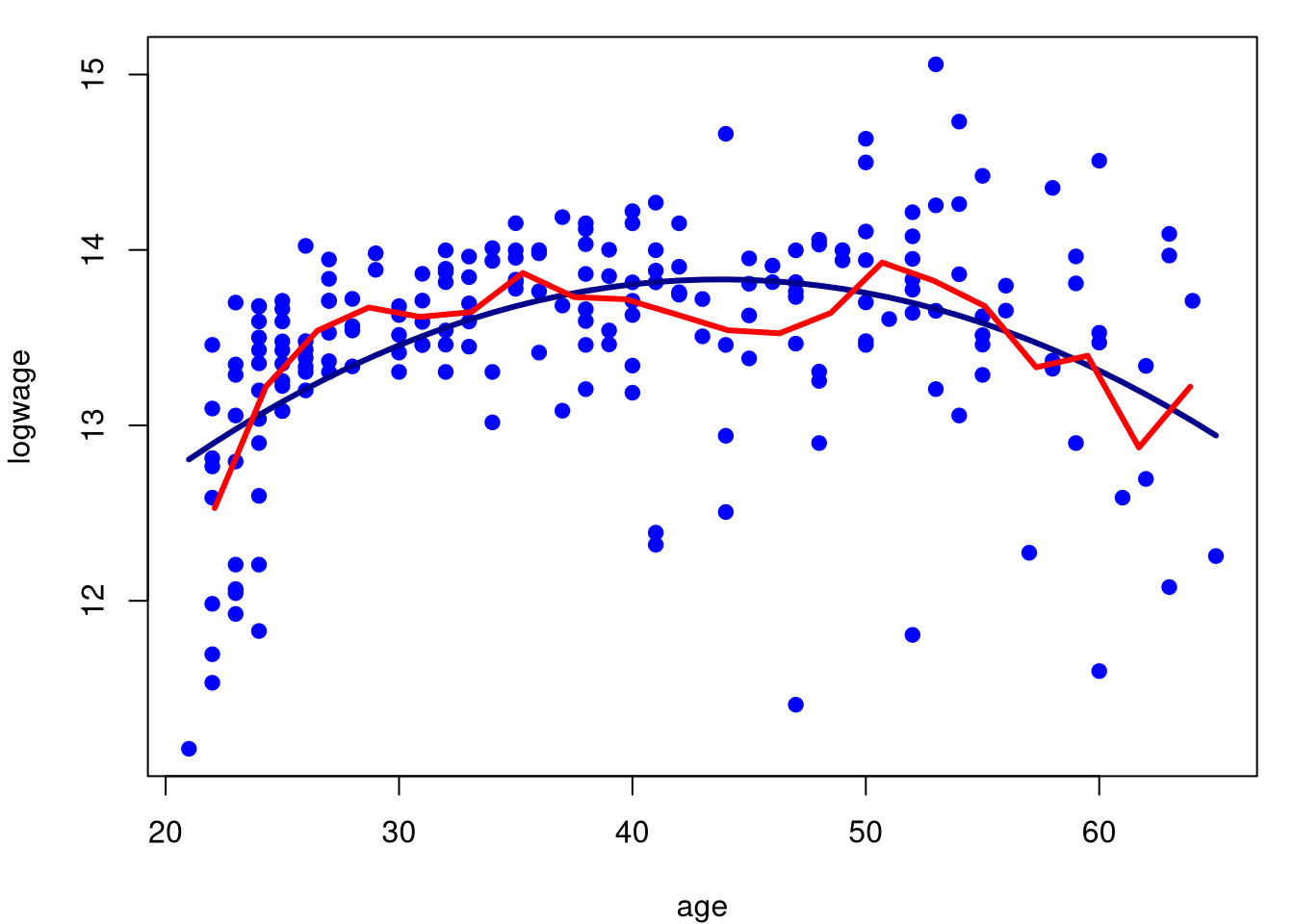
Podemos perceber com este exemplo que o regressograma aproxima-se do modelo paramétrico, embora o regressograma sirva mais como descrição dos dados e não como interpretação. O regressograma não é a única forma de encontrarmos um suavizamento linear. Vejamos no seguinte exemplo uma outra forma de definirmos um destes modelos.
Exemplo 4. (Médias locais)
Fixemos \(h> 0\) e \(B_x = \{i \, : \, |x_i-x|\leq h\}\). Seja \(n_x\) o número de pontos em \(B_x\). Para qualquer \(x\), para o qual \(n_x> 0\), definamos \[\begin{equation} \widehat{r}_n(x) \, = \, \frac{1}{n_x}\sum_{i\in B_x} Y_i\cdot \end{equation}\] Este é o estimador médio local de \(r(x)\), um caso especial do estimador kernel a ser discutido em breve. Nesse caso, \(\widehat{r}_n(x) = \sum_{i=1}^n Y_i\mathcal{l}_i(x)\) onde \(\mathcal{l}_i(x) = 1 / n_x\) se \(|x_i - x |\leq h\) e \(\mathcal{l}_i(x) = 0\) caso contrário.
Como exemplo simples, suponha que \(n = 9\), \(x_i = i / 9\) e \(h = 1/9\). Então, \[\begin{equation} L \, = \, \begin{pmatrix} 1/2 & 1/2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1/3 & 1/3 & 1/3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1/3 & 1/3 & 1/3 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1/3 & 1/3 & 1/3 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1/3 & 1/3 & 1/3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1/3 & 1/3 & 1/3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1/3 & 1/3 & 1/3 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1/3 & 1/3 & 1/3 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1/2 & 1/2 \end{pmatrix}\cdot \end{equation}\]
Maiores detalhes ver o lvro de Fan & Gijbels (1996).
2.1 Avaliando a qualidade do ajuste
É desejável usar uma medida, livre de unidade, para mensurar a adequação de modelos de regressão não paramétricos que seja comparável àquela usada para modelos de regressão paramétricos, a saber, \(R^2\). Note que esta será uma medida dentro da amostra da qualidade de ajuste.
Dadas as desvantagens conhecidas de computar \(R^2\) com base na decomposição da soma dos quadrados, existe uma definição e um método alternativos para calcular \(R^2\), que pode ser usado diretamente para qualquer modelo, linear ou não linear.
Definição 3. Seja \(Y_i\) a resposta e \(\widehat{r}_n(x_i)\) a resposta estimada para a \(i\)-ésima observação. Definimos \(R^2\) como segue: \[\begin{equation} R^2 \, = \, \frac{\displaystyle \Big( \sum_{i=1}^n (y_i-\overline{y})(\widehat{r}_n(x_i)-\overline{y})\Big)^2} {\displaystyle \sum_{i=1}^n (y_i-\overline{y})^2 \sum_{i=1}^n (\widehat{r}_n(x_i)-\overline{y})^2}, \end{equation}\] onde \(y_1,\cdots,y_n\) sãs observações da resposta e \(\overline{y}\) a média amostral.
Esta medida estará sempre no intervalo \([0,1]\), com o valor 1 denotando um ajuste perfeito aos dados da amostra e 0 denotando nenhum poder preditivo acima daquele dado pela média incondicional da resposta. Pode ser demonstrado que este método de cálculo do \(R^2\) é idêntico à medida padrão computada como \[\begin{equation} \sum_{i=1}^n (\widehat{\mu}_i-\overline{y})^2/\sum_{i=1}^n (y_i-\overline{y})^2 \end{equation}\] quando o modelo é linear, obtido por mínimos quadrados e incluindo o termo do intercepto. Nesta expressão \(\widehat{\mu}=X\widehat{\beta}\) é o vetor de estimativas do preditor linear.
Esta medida útil permitirá a comparação direta entre a adequação da amostra e a qualificação óbvia de que este não é, de forma alguma, um critério de seleção de modelos e sim simplesmente uma medida resumida que podemos relatar.
Devemos observar que em situações nas quais agrupamos informações, como é o caso do regressograma, não é possível utilizarmos este coeficiente.
2.2 Escolhendo o parâmetro de suavização
Os suavizadores que usaremos dependerão de algum parâmetro de suavização e precisaremos de alguma maneira de escolher \(h\). Definamos o risco como o erro quadrático médio \[\begin{equation} R(h) \, = \, \mbox{E}\Big( \frac{1}{n}\sum_{i=1}^n \big( \widehat{r}_n(x_i)-r(x_i)\big)^2 \Big)\cdot \end{equation}\]
Idealmente, gostaríamos de escolher \(h\) como aquele que minimizar \(R(h)\), mas \(R(h)\) depende da função desconhecida \(r(x)\). Em vez disso, minimizaremos uma estimativa \(\widehat{R}(h)\) de \(R(h)\). Como primeiro palpite, podemos usar a média da soma de quadrados dos resíduos, também chamadas de erro de treinamento \[\begin{equation} \frac{1}{n}\sum_{i=1}^n \big( Y_i-\widehat{r}_n(x_i)\big)^2 \end{equation}\] para estimar \(R(h)\).
Isto acaba por ser uma estimativa pobre de \(R(h)\): é tendenciosa para baixo e tipicamente leva a subsuavizamento ou sobreajuste. A razão é que estamos usando os dados duas vezes: para estimar a função e estimar o risco. A estimativa da função é escolhida para fazer \(\sum_{i=1}^n \big( Y_i-\widehat{r}_n(x_i)\big)^2\) pequeno, o que tenderá a subestimar o risco. Estimaremos o risco usando validação cruzada, que é definida da seguinte forma.
Definição 4. O estimador de validação cruzada do risco é definido por \[\begin{equation} \widehat{R}(h) \, = \, \frac{1}{n}\sum_{i=1}^n \big( Y_i-\widehat{r}_{-i}(x_i)\big)^2, \end{equation}\] onde \(\widehat{r}_{-i}\) é o estimador obtido omitindo o \(i\)-ésimo par \((x_i,Y_i)\).
Como dito acima, esta definição está incompleta. Nós não dissemos o que queremos dizer precisamente por \(\widehat{r}_{-i}\). Vamos definir \[\begin{equation} \widehat{r}_{-i}(x) \, = \, \sum_{j=1}^n Y_j\mathcal{l}_{j,(-i)}(x), \end{equation}\] onde \[\begin{equation} \mathcal{l}_{j,(-i)}(x) \, = \, \left\{ \begin{array}{cc} 0, & \mbox{ se } j = i \\ \frac{\displaystyle\mathcal{l}_j(x)}{\displaystyle\sum_{k\neq i} \mathcal{l}_k(x)}, & \mbox{ se } j\neq i \end{array}\right.\cdot \end{equation}\]
Em outras palavras, definimos o peso em \(x_i\) para 0 e renormalizamos os outros pesos para somar um. Para todos os métodos a serem considerados: regressão kernel, polinómios locais e suavização por splines, essa forma para \(\widehat{r}_{-i}\) pode realmente ser derivada como uma propriedade do método, em vez de uma questão de definição. É mais simples tratar isso como uma definição.
A intuição da validação cruzada é a seguinte. Observe que \[\begin{equation} \begin{array}{rcl} \mbox{E}\big( Y_i-\widehat{r}_{-i}(x_i)\big)^2 & = & \mbox{E}\big( Y_i-r(x_i)+r(x_i)-\widehat{r}_{-i}(x_i)\big)^2 \\ & = & \sigma^2 \, + \, \mbox{E}\big( r(x_i)-\widehat{r}_{-i}(x_i)\big)^2 \, \approx \, \sigma^2 \, + \, \mbox{E}\big( r(x_i)-\widehat{r}_n(x_i)\big)^2, \end{array} \end{equation}\] e, portanto, \[\begin{equation} \mbox{E}(\widehat{R}) \, \approx \, R \, + \, \sigma^2 \, = \, \mbox{risco preditivo}\cdot \end{equation}\] Assim, o escore de validação cruzada é uma estimativa quase imparcial do risco.
Parece ser demorado avaliar \(\widehat{R}(h)\). Isto devido a que, aparentemente, precisamos recomputar o estimador após abandonar cada observação. Felizmente, existe uma fórmula de atalho para calcular \(\widehat{R}\) para suavizadores lineares e será apresentada no seguinte teorema.
Teorema 2. Seja \(\widehat{r}_n\) um suavizador linear. Então, o estimador de validação cruzada do risco \(\widehat{R}(h)\) pode ser escrito como \[\begin{equation} \widehat{R}(h) \, = \, \frac{1}{n}\sum_{i=1}^n \Big( \frac{Y_i-\widehat{r}_n(x_i)}{1-L_{ii}}\Big)^2, \end{equation}\] onde \(L_{ii}=\mathcal{l}_i(x_i)\) é o \(i\)-ésimo elemento da diagonal principal da matriz de suavização \(L\).
Demonstração. Ver Fan and Gijbels (1996).
O parámetro de suavização \(h\) pode ser escolhido minimizando \(\widehat{R}(h)\). É importante notar que não podemos supor que \(\widehat{R}(h)\) sempre tenha um mínimo bem definido. Devemos sempre traçar \(\widehat{R}(h)\) como uma função de \(h\). Embora interessante, não será desta maneira que encontraremos o valor estimado do parámetro de suavização.
Em vez de minimizar o escore de validação cruzada, uma alternativa é usar uma aproximação chamada validação cruzada generalizada na qual cada \(L_{ii}\) na equação do Teorema 2 é substituída por sua média \(\frac{1}{n}\sum_{i=1}^n L_{ii} = \nu/n\), onde \(\nu = \mbox{tr}(L)\) são os graus efetivos de liberdade. Assim, nós minimizaríamos \[\begin{equation} GCV(h) \, = \, \frac{1}{n}\sum_{i=1}^n \frac{1}{n}\sum_{i=1}^n \Big( \frac{Y_i-\widehat{r}_n(x_i)}{1-\nu/n}\Big)^2 \cdot \end{equation}\]
Geralmente, a largura de banda \(\widehat{h}\) que minimiza o escore de validação cruzada generalizada está próximo da largura de banda que minimiza a validação cruzada.
Utilizando a aproximação \((1-x)^{-2} \approx 1+2x\) vemos que \[\begin{equation} GCV(h) \, \approx \, \frac{1}{n}\sum_{i=1}^n \big( Y_i-\widehat{r}_n(x_i)\big)^2 \, + \, \frac{2\nu\widehat{\sigma}^2}{n} \, = \, C_p, \end{equation}\] onde \(\widehat{\sigma}^2=n^{-1}\sum_{i=1}^n \big( Y_i-\widehat{r}_n(x_i)\big)^2\).
A equação acima é conhecida como a estatística \(C_p\) a qual foi originalmente proposta por Colin Mallows como critério para selecionar variáveis nos modelos de regressã linear. Mais geralmente, muitos critérios comuns de seleção de largura de banda podem ser escritos na forma \[\begin{equation} B(h) \, = \, \mathcal{D}(n,h)\times \frac{1}{n}\sum_{i=1}^n \big( Y_i-\widehat{r}_n(x_i)\big)^2, \end{equation}\] para diferentes escolhas de \(\mathcal{D}(n,h)\). Veja Härdle et al. (1988) para detalhes. Além disso, Härdle et al. (1988) provaram que, sob condições adequadas, os seguintes fatos sobre o valor de \(\widehat{h}\) que minimiza \(B(h)\).
Seja \(\widehat{h}_0\) o valor de \(\widehat{h}\) que minimiza a perda \(L(\widehat{h}) = n^{-1}\sum_{i=1}^n \big(\widehat{r}_n(x_i)-r(x_i)\big)^2\), e seja \(h_0\) o risco mínimo. Então para todo \(\widehat{h}\), \(\widehat{h}_0\) e \(h_0\) tendem a 0 na taxa \(n^{−1/5}\). Além disso, para certas constantes positivas \(C_1\), \(C_2\), \(\sigma_1\) e \(\sigma_2\), temos que \[\begin{equation} \begin{array}{cc} n^{3/10}\big(\widehat{h}-\widehat{h}_0\big) \, \approx \, N(0,\sigma_1^2), & \qquad n\big(L(\widehat{h})-L(\widehat{h}_0)\big) \, \approx \, C_1\chi_1^2 \\ n^{3/10}\big(h_0-\widehat{h}_0\big) \, \approx \, N(0,\sigma_2^2), & \qquad n\big(L(h_0)-L(\widehat{h}_0)\big) \, \approx \, C_2\chi_1^2 \cdot \end{array} \end{equation}\]
Assim, a taxa relativa de convergência de \(\widehat{h}\) é \[\begin{equation} \frac{\widehat{h}-\widehat{h}_0}{\widehat{h}_0} \, = \, O_P\Big(\frac{n^{3/10}}{n^{1/5}} \Big) \, = \, O_P(n^{-1/10})\cdot \end{equation}\] Essa taxa lenta mostra que é difícil estimar a largura de banda. Essa taxa é intrínseca ao problema de seleção de largura de banda, isto deve-se a que também é verdade que \[\begin{equation} \frac{\widehat{h}_0-h_0}{h_0} \, = \, O_P\Big(\frac{n^{3/10}}{n^{1/5}} \Big) \, = \, O_P(n^{-1/10})\cdot \end{equation}\]